Η αναζήτηση βρήκε 261 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Τρί Φεβ 01, 2011 5:29 pm
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: Διαγωνισμός Αρχιμήδης - Των φρονίμων τα παιδιά...!
- Απαντήσεις: 241
- Προβολές: 40853
Re: Διαγωνισμός Αρχιμήδης 2011 - Των φρονίμων τα παιδιά...!
28. Να βρεθούν όλοι οι πρώτοι αριθμοί $p$ τέτοιοι ώστε ο αριθμός $p^3-p+1$ να είναι τέλειο τετράγωνο ακεραίου. Ο χρόνος μου είναι περιορισμένος οπότε γράφω τη λύση σχετικά συνοπτικά. Θέλουμε $p^3-p=s^2-1 \Leftrightarrow (p-1)p(p+1)=(s-1)(s+1)$. Αφού ο $p$ είναι πρώτος προκύπτει πως διαιρεί έναν του...
- Πέμ Ιαν 27, 2011 9:45 pm
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: Διαγωνισμός Αρχιμήδης - Των φρονίμων τα παιδιά...!
- Απαντήσεις: 241
- Προβολές: 40853
Re: Διαγωνισμός Αρχιμήδης 2011 - Των φρονίμων τα παιδιά...!
24. Να βρεθούν οι μη αρνητικές ακέραιες λύσεις της εξίσωσης $7^a=4^b+5^c+6^d$. Αν $d\neq 0$ τότε εξετάζοντας τη δοθείσα $mod 3$ παίρνουμε $7^a \equiv 1 \equiv 1^b+(-1)^c (mod 3)$, άτοπο. Άρα $d=0$. Αν $a=0$ τότε $1=4^b+5^c+1$, άτοπο. Άρα $a \neq 0$. Αν $b \neq 0$ τότε $(-1)^a \equiv 7^a \equiv 4^b+...
- Παρ Ιαν 21, 2011 11:25 am
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Εξίσωση Ναί!!
- Απαντήσεις: 1
- Προβολές: 261
Re: Εξίσωση Ναί!!
Κατ' αρχάς παρατηρούμε ότι αν η $(x,y,z)$ αποτελεί λύση τότε και η $(\pm x, \pm y, \pm z)$ αποτελεί λύση. Ψάχνουμε επομένως για λύσεις στους μη αρνητικούς ακεραίους. Κάνοντας πράξεις παίρνουμε: $x^4y^2+2x^2y^2z^2=x^2+x^2y^2+x^4y^4z^4$. Αν $x=0$ παίρνουμε τη λύση $(x,y,z)=(0,y,z)$, με $y,z$ τυχαίους ...
- Τετ Ιαν 19, 2011 11:56 pm
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: Διαγωνισμός Αρχιμήδης - Των φρονίμων τα παιδιά...!
- Απαντήσεις: 241
- Προβολές: 40853
Re: Διαγωνισμός Αρχιμήδης - Των φρονίμων τα παιδιά...!
2. Αν $\displaystyle{n}$ είναι θετικός ακέραιος, να αποδείξετε ότι $\displaystyle{1\cdot \frac{1}{2^2}\cdot \frac{1}{3^3}\cdot \frac{1}{4^4}\cdots \frac{1}{n^n}<\left(\frac{2}{n+1} \right)^{\frac{n(n+1)}{2}}.}$ Διαφορετικά, με την ΑΜ-ΓΜ έχουμε πως $\displaystyle \frac{2}{n+1}=\frac{n}{\frac{n(n+1)}...
- Σάβ Ιαν 15, 2011 1:48 pm
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: ΕΥΚΛΕΙΔΗΣ 2010 - 2011
- Απαντήσεις: 111
- Προβολές: 14469
Re: ΕΥΚΛΕΙΔΗΣ 2010 - 2011
Εγώ έδινα στην Γ' Λυκείου. Προσωπικά τα βρήκα ευκολότερα από τα περσινά της Γ'. Στο 1ο θέμα έδωσα την ίδια λύση με την επίσημη. Το 2ο θέμα το έλυσα λύνοντας την δεύτερη εξίσωση ως προς $x$ και αντικαθιστώντας στην πρώτη. Άσχημη λύση βέβαια αλλά δεν έχασα ρίζες. Στο 3ο θέμα απέδειξα την ισότητα των $...
- Δευ Ιαν 10, 2011 5:36 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: 2 Προκλήσεις από το Οπερ εδει δειξαι
- Απαντήσεις: 2
- Προβολές: 441
Re: 2 Προκλήσεις από το Οπερ εδει δειξαι
Εξαιρετικό θέμα το 2ο. Από τον ορισμό της ισότητας μιγαδικών το σύστημα ισοδυναμεί με την εξίσωση: $\displaystyle xi+y=i+\frac{xi-yi}{x^2+y^2}+2-\frac{x+y}{x^2+y^2} \Leftrightarrow xi+y=2+i+\frac{xi-y-x-yi}{x^2+y^2}$ Θέτω $\displaystyle z=x-yi$ και τότε $xi+y=iz$, $xi-y=i\overline{z}$ και $x+yi=\ove...
- Σάβ Ιαν 08, 2011 2:40 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: 'Υπαρξη ακεραίων
- Απαντήσεις: 1
- Προβολές: 208
- Τετ Ιαν 05, 2011 3:40 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Συναρτησιακές----->Bulletin(1/?)
- Απαντήσεις: 173
- Προβολές: 23383
Re: Συναρτησιακές---------------->Bulletin(1/?)
Λυση για την 49: Εφαρμοζοντας την αρχικη για $y=-f(x)$ προκυπτει: $f(0)=2x+f(f(f(-f(x)))-x)$ απο οπου προκυπτει οτι η $f$ ειναι συναρτηση επι του $R$. ... απο οπου προκυπτει οτι η $f$ ειναι $1-1$. Νομίζω ότι στην πολύ ωραία λύση του Σάκη μπορούμε να δείξουμε το $1-1$ και ως εξής: Έστω $a,b, c \in R...
- Κυρ Ιαν 02, 2011 7:53 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Τέλειο τετράγωνο
- Απαντήσεις: 2
- Προβολές: 508
Re: Τέλειο τετράγωνο
Για $n=2$ το ζητούμενο ισχύει ενώ για $n=1$ όχι. Αν ο ζητούμενος αριθμός είναι τετράγωνο, τότε τετράγωνο θα είναι και ο $4(n^4+n^3-8)$. Έχουμε πως $4n^4+4n^3-32 <(2n^2+n)^2 \Leftrightarrow n^2+32 >0$, που ισχύει. Επίσης $4n^4+4n^3-32 >(2n^2+n-2)^2 \Leftrightarrow (7n+18)(n-2) >0$ που ισχύει. Άρα θα ...
- Πέμ Δεκ 30, 2010 1:39 am
- Δ. Συζήτηση: Ασκήσεις ΜΟΝΟ για μαθητές
- Θέμα: Eξίσωση
- Απαντήσεις: 3
- Προβολές: 845
Re: Eξίσωση
Θέτοντας $a=2^x$ και $b=3^x$ η εξίσωση γίνεται: $27a^3-b^3-27-27ab=0$ ή αλλιώς $(3a)^3+(-b)^3+(-3)^3+3(3a)(-b)(-3)=0$ που είναι η ταυτότητα του Euler. Άρα πρέπει είτε $3a=-b=-3$ που δεν οδηγεί σε λύσεις είτε $3a-b-3=0 \Leftrightarrow 2^x=3^{x-1}+1$. Η $\displaystyle f(x)=\big(\frac{3}{2}\big)^{x-1}+...
- Πέμ Δεκ 30, 2010 1:04 am
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: ΑΣΚΗΣΗ ΑΠΟ ΣΟΥΗΔΙΑ
- Απαντήσεις: 7
- Προβολές: 835
Re: ΑΣΚΗΣΗ ΑΠΟ ΣΟΥΗΔΙΑ
Διαφορετικά, το πολυώνυμό μας ισούται με το μονίμως θετικό 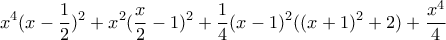 .
.
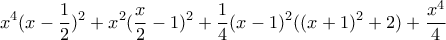 .
.- Τετ Δεκ 29, 2010 1:41 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Μία ανισότητα!
- Απαντήσεις: 4
- Προβολές: 541
Re: Μία ανισότητα!
Με χρήση παραγώγων (ή του wolframalpha  ) προκύπτει ότι
) προκύπτει ότι
 για κάθε θετικό
για κάθε θετικό  . Η ισότητα ισχύει όταν
. Η ισότητα ισχύει όταν  .
.
Προσθέτοντας τις αντίστοιχες ανισότητες για τα προκύπτει το ζητούμενο (αφού
προκύπτει το ζητούμενο (αφού 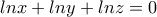 ).
).
 για κάθε θετικό
για κάθε θετικό  . Η ισότητα ισχύει όταν
. Η ισότητα ισχύει όταν  .
.Προσθέτοντας τις αντίστοιχες ανισότητες για τα
 προκύπτει το ζητούμενο (αφού
προκύπτει το ζητούμενο (αφού 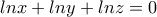 ).
).- Τετ Δεκ 29, 2010 1:17 am
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Μία ανισότητα!
- Απαντήσεις: 4
- Προβολές: 541
Re: Μία ανισότητα!
Να προτείνω και την ακόλουθη.
Αν με
με  να δείξετε ότι
να δείξετε ότι

Αν
 με
με  να δείξετε ότι
να δείξετε ότι
- Τετ Δεκ 29, 2010 12:57 am
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Juniors) - Παλαιότερες Συζητήσεις
- Θέμα: Πρώτοι αριθμοί
- Απαντήσεις: 1
- Προβολές: 266
Re: Πρώτοι αριθμοί
Αφού για κάθε φυσικό $n$ είναι $n^4 \equiv 0,1 (mod 16)$, αν κανένας από τους $a,b,c$ δεν είναι $2$ έχουμε $a^4+b^4+c^4-3 \equiv 1+1+1-3 \equiv 0 (mod 16)$, άρα τουλάχιστον ένας εξ αυτών ισούται με το $2$, έστω ο $c$. Αφού για κάθε φυσικό $n$ είναι $n^4 \equiv 0,1 (mod 3)$, αν κανένας από τους $a,b$...
- Δευ Δεκ 27, 2010 11:59 pm
- Δ. Συζήτηση: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΑ - ΣΥΝΕΧΕΙΑ
- Θέμα: Ύπαρξη αριθμού
- Απαντήσεις: 3
- Προβολές: 505
Re: Ύπαρξη αριθμού
Για την $\displaystyle g(x)=2x^2-x+1$ είναι $\displaystyle g([0,1])=\Big[\frac{7}{8},2\Big]$ (απλό με μονοτονία). Από το Θ.Ε.Τ υπάρχουν $\displaystyle x_1, x_2 \in [0,1]$ τέτοια ώστε $\displaystyle f(x_1)=\frac{7}{8}$ και $f(x_2)=2$. Θεωρώντας την συνεχή $h(x)=f(x)-2x^2+x-1$ παίρνουμε λόγω των προηγ...
- Παρ Δεκ 24, 2010 9:32 pm
- Δ. Συζήτηση: Θέματα για Λύκειο - Seniors
- Θέμα: Ανισότητες
- Απαντήσεις: 8
- Προβολές: 1160
Re: Ανισότητες
Για την 6η, με κάποια επιφύλαξη: Από την Cauchy Schwarz έχουμε πως $(a+b+c)(a^3+b^3+c^3) \geq (a^2+b^2+c^2)^2$. Αρκεί επομένως να αποδείξουμε ότι $(a^2+b^2+c^2)^3 \geq 4(a^6+b^6+c^6)$. Επειδή το τρίγωνο είναι οξυγώνιο, έχουμε πως $a^2+b^2 > c^2$ και κυκλικά και άρα υπάρχουν $x,y,z$ τέτοιοι ώστε $a^2...
- Παρ Δεκ 24, 2010 8:59 pm
- Δ. Συζήτηση: Θέματα για Λύκειο - Seniors
- Θέμα: Ανισότητες
- Απαντήσεις: 8
- Προβολές: 1160
Re: Ανισότητες
Στην 5η, το $3$ στο δεξί μέλος πρέπει να αντικατασταθεί από το $\sqrt{3}$. Για οποιουσδήποτε πραγματικούς $a,b$ ισχύει ότι $4(a^2+ab+b^2) \geq 3(a+b)^2$ αφού ισοδύναμα γράφεται $(a-b)^2 \geq 0$. Παίρνοντας ρίζες $\sqrt{a^2+ab+b^2} \geq \frac{\sqrt{3}}{2}(a+b)$. Άρα $\displaystyle \sum a\sqrt{b^2+bc+...
- Παρ Δεκ 24, 2010 8:39 pm
- Δ. Συζήτηση: Θέματα για Λύκειο - Seniors
- Θέμα: Ανισότητες
- Απαντήσεις: 8
- Προβολές: 1160
Re: Ανισότητες
Μία λύση για την 4η. Είναι $\displaystyle \frac{a-2}{a+1}=1-\frac{3}{a+1}$ οπότε η ανισότητα γίνεται $\displaystyle \sum \frac{1}{a+1} \geq 1$. Από τη συνθήκη προκύπτει ότι υπάρχουν θετικοί $x, y, z$ τέτοιοι ώστε $\displaystyle a=\frac{2x}{y}$, $\displaystyle b=\frac{2y}{z}$ και $\displaystyle c=\fr...
- Πέμ Δεκ 23, 2010 10:52 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Ανισότητα!
- Απαντήσεις: 2
- Προβολές: 341
Re: Ανισότητα!
Θεωρώ την $\displaystyle f(x)=ln\frac{x}{1-x}$ στo $\displaystyle \Big(0,\frac{1}{2}\Big]$ στο οποίο είναι κοίλη αφού $\displaystyle f^{''}(x)=\frac{2x-1}{(x-x^2)^2} \leq 0$. Από την ανισότητα Jensen, επομένως, παίρνουμε: ${\displaystyle \sum_{j=1}^{n}ln\frac{x_j}{1-x_j} \leq nln\frac{\displaystyle ...
- Πέμ Δεκ 23, 2010 12:54 am
- Δ. Συζήτηση: Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)
- Θέμα: Θέματα Ευκλείδη Γ' Λυκείου 2008
- Απαντήσεις: 5
- Προβολές: 985
Re: Θέματα Ευκλείδη Γ' Λυκείου 2008
Για το τρίτο σχηματίζουμε όλες τις διαδοχικές διαφορές των όρων της ακολουθίας. Τις προσθέτουμε και παίρνουμε: $a_{n+1}-a_1=2\frac{n(n+1)}{2}+n \Leftrightarrow a_{n+1}=(n+1)^2+a_1-1 \Leftrightarrow a_{n}=n^2+c$, όπου $c=a_1-1$. Άρα $\displaystyle a_{n}a_{n+1}=(n^2+c)(n^2+2n+1+c)=(n^2+n+c)^2+c=a_{n^2...
