 είναι ένα πεπερασμένο σώμα, τότε κάθε στοιχείο του
είναι ένα πεπερασμένο σώμα, τότε κάθε στοιχείο του  γράφεται ως άθροισμα δύο τετραγώνων (στοιχείων του
γράφεται ως άθροισμα δύο τετραγώνων (στοιχείων του  ).
).Συντονιστής: Demetres
 είναι ένα πεπερασμένο σώμα, τότε κάθε στοιχείο του
είναι ένα πεπερασμένο σώμα, τότε κάθε στοιχείο του  γράφεται ως άθροισμα δύο τετραγώνων (στοιχείων του
γράφεται ως άθροισμα δύο τετραγώνων (στοιχείων του  ).
). .
. ,είναι κυκλική.
,είναι κυκλική. Για
Για  : Θα έχουμε
: Θα έχουμε  περιττός.
περιττός.  με
με  . Εύκολα βλέπουμε ότι η
. Εύκολα βλέπουμε ότι η  είναι ομομορφισμός ομάδων και επιπλέον
είναι ομομορφισμός ομάδων και επιπλέον  με το τελευταίο να ισχύει διότι αν υπήρχε
με το τελευταίο να ισχύει διότι αν υπήρχε  με
με  , τότε από το θεώρημα του Lagrange θα είχαμε
, τότε από το θεώρημα του Lagrange θα είχαμε  , άτοπο.
, άτοπο. είναι και επί, άρα κάθε στοιχείο του
είναι και επί, άρα κάθε στοιχείο του  είναι τετράγωνο. (το
είναι τετράγωνο. (το  είναι κατά τετριμμένο τρόπο), άρα έχουμε το ζητούμενο.
είναι κατά τετριμμένο τρόπο), άρα έχουμε το ζητούμενο. Για
Για  :
:  ομάδα με
ομάδα με  και
και  με
με  . Τότε
. Τότε  .
. . Έστω
. Έστω  . Θεωρώ το
. Θεωρώ το  .
. με
με  , βλέπουμε εύκολα ότι είναι
, βλέπουμε εύκολα ότι είναι  και επί του
και επί του  , άρα
, άρα  .
. . Ισχυρίζομαι ότι
. Ισχυρίζομαι ότι  .
. , άρα
, άρα  , άτοπο.
, άτοπο.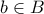 είναι
είναι  , άρα
, άρα  και παίρνουμε το ζητούμενο.
και παίρνουμε το ζητούμενο. πρώτο τώρα, θα είναι
πρώτο τώρα, θα είναι  άρτιος. Αφού η
άρτιος. Αφού η  είναι κυκλική, τετράγωνα θα είναι τα στοιχεία της
είναι κυκλική, τετράγωνα θα είναι τα στοιχεία της  που είναι άρτιες δυνάμεις του γεννήτορα, συν το
που είναι άρτιες δυνάμεις του γεννήτορα, συν το  , άρα
, άρα  το πλήθος τα οποία αποτελούν το σύνολο έστω
το πλήθος τα οποία αποτελούν το σύνολο έστω  .
. και
και  την προσθετική ομάδα των στοιχείων του σώματος παίρνουμε το ζητούμενο.
την προσθετική ομάδα των στοιχείων του σώματος παίρνουμε το ζητούμενο. όπου ο
όπου ο  είναι πρώτος και ο
είναι πρώτος και ο  θετικός ακέραιος. Διακρίνουμε δύο περιπτώσεις:
θετικός ακέραιος. Διακρίνουμε δύο περιπτώσεις: Έστω ότι
Έστω ότι  οπότε η χαρακτηριστική του σώματος
οπότε η χαρακτηριστική του σώματος  είναι ίση με
είναι ίση με  Τότε, η απεικόνιση
Τότε, η απεικόνιση 
 ισχύουν
ισχύουν
 )
)
 είναι πεπερασμένο, η
είναι πεπερασμένο, η  θα είναι και επί. Άρα για κάθε
θα είναι και επί. Άρα για κάθε  θα υπάρχει
θα υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  και το συμπέρασμα έπεται.
και το συμπέρασμα έπεται. Έστω ότι
Έστω ότι  Θεωρούμε τυχαίο, αλλά σταθεροποιημένο
Θεωρούμε τυχαίο, αλλά σταθεροποιημένο  και θέτουμε:
και θέτουμε:



 τέτοια, ώστε
τέτοια, ώστε  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. ένα τυχόν στοιχείο του
ένα τυχόν στοιχείο του  . Θέλουμε να δείξουμε ότι το
. Θέλουμε να δείξουμε ότι το  είναι άθροισμα δύο τετραγώνων. Κοιτάμε το πολυώνυμο
είναι άθροισμα δύο τετραγώνων. Κοιτάμε το πολυώνυμο
 . Ο συντελεστής του
. Ο συντελεστής του  είναι
είναι  . Ισχυρίζομαι ότι αυτός ο συντελεστής είναι διάφορος του μηδενός (στο
. Ισχυρίζομαι ότι αυτός ο συντελεστής είναι διάφορος του μηδενός (στο  ). Πράγματι αν
). Πράγματι αν  τότε η μεγαλύτερη δύναμη του
τότε η μεγαλύτερη δύναμη του  που διαιρεί το
που διαιρεί το  ισούται με
ισούται με  .
. (και
(και  ) και παίρνουμε ότι υπάρχουν
) και παίρνουμε ότι υπάρχουν  ώστε
ώστε  . Αυτό όμως θα μπορούσε να συμβεί μόνο αν
. Αυτό όμως θα μπορούσε να συμβεί μόνο αν  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες