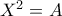 ,
, όπου

(Μπορεί κάποιος να βοηθήσει σχετικά με την λύση εξισώσεων παρόμοιας μορφής;)
Συντονιστής: Demetres
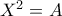 ,
, 
 είναι σε κανονική μορφή Jordan βοηθάει αρκετά.
είναι σε κανονική μορφή Jordan βοηθάει αρκετά.  όπου
όπου 
 από Cayley-Hamilton.
από Cayley-Hamilton.  άρα καταλήγουμε στο ότι
άρα καταλήγουμε στο ότι  . Επειδή
. Επειδή  παίρνουμε
παίρνουμε
 και
και  .
.
Η λύση του Δημήτρη είναι η συντομότερη δυνατή γιατί χρησιμοποιεί το ότι ο πίνακαςgeorgevg έγραψε:..Μπορεί κάποιος να βοηθήσει σχετικά με την λύση εξισώσεων παρόμοιας μορφής;
 είναι σε κανονική μορφή Jordan. Στην γενικότερη περίπτωση όπου ο πίνακας
είναι σε κανονική μορφή Jordan. Στην γενικότερη περίπτωση όπου ο πίνακας  είναι διαγωνοποιήσιμος και θετικά ημιορισμένος, η διαδικασία έχει περισσότερους υπολογισμούς και βήματα:
είναι διαγωνοποιήσιμος και θετικά ημιορισμένος, η διαδικασία έχει περισσότερους υπολογισμούς και βήματα:  είναι διαγωνοποιήσιμος και θετικά ορισμένος, υπάρχει διαγώνιος πίνακας
είναι διαγωνοποιήσιμος και θετικά ορισμένος, υπάρχει διαγώνιος πίνακας  -με τις μη-αρνητικές ιδιοτιμές του
-με τις μη-αρνητικές ιδιοτιμές του  στην διαγώνιό του- και αντιστρέψιμος πίνακας
στην διαγώνιό του- και αντιστρέψιμος πίνακας  , έτσι ώστε
, έτσι ώστε  .
. 
Επίσης, επειδή η διάσταση του πίνακα είναι τόσο μικρή, μπορείς να αναζητήσεις τις λύσεις υπό τη μορφήgeorgevg έγραψε:Να βρεθούν οι τετραγωνικοί πίνακες που ικανοποιούν την σχέση:,
όπου
(Μπορεί κάποιος να βοηθήσει σχετικά με την λύση εξισώσεων παρόμοιας μορφής;)
 ,
, .
. .
. και από την πρώτη
και από την πρώτη 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες