Δεν ισχύει για κάθε Α και Β;

Mathletic · #1

Γειά σας!!

Έχω δείξει ότι για $A,B\in \mathbb{R}^{2\times 2}$ το $U=\{X\in \mathbb{R}^{2\times 2}\mid AX=XB\}$ είναι διανυσματικός υπόχωρος του $\mathbb{R}^{2\times 2}$ ως εξής:

Είναι μη-κενό, επειδή ο μηδενικός πίνακας ανήκει στο

:

.

Έστω $X_1, X_2\in U$ τότε AX_1=X_1B

και

.
Έχουμε ότι A(X_1+X_2)=AX_1+AX_2=X_1B+X_2B=(X_1+X_2)B

, και άρα $X_1+X_2\in U$ .

Έστω $\lambda \in \mathbb{R}$ .
Έχουμε ότι $A(\lambda X_1)=\lambda (AX_1)=\lambda (X_1B)=(\lambda X_1)B$ , και άρα $\lambda X_1\in U$ .

Όταν $A=\begin{pmatrix}a_1 & 0 \\ a_3 & a_4\end{pmatrix}$ και $B=\begin{pmatrix}b_1 & b_2 \\ 0 & b_4\end{pmatrix}$ θέλω να δείξω ότι $U=\{0\} \iff \{a_1, a_4\}\cap \{b_1, b_4\}=\emptyset$

Έχουμε ότι
$AX=\begin{pmatrix}a_1 & 0 \\ a_3 & a_4\end{pmatrix}\begin{pmatrix}x_1 & x_2 \\ x_3 & x_4\end{pmatrix}=\begin{pmatrix}a_1x_1 & a_1x_2 \\ a_3x_1+a_4x_3 & a_3x_2+a_4x_4\end{pmatrix}$
και
$XB=\begin{pmatrix}x_1 & x_2 \\ x_3 & x_4\end{pmatrix}\begin{pmatrix}b_1 & b_2 \\ 0 & b_4\end{pmatrix}=\begin{pmatrix}x_1b_1 & x_1b_2+x_2b_4 \\ x_3b_1 & x_3b_2+x_4b_4\end{pmatrix}$

Άρα
$AX=XB \Rightarrow \begin{pmatrix}a_1x_1 & a_1x_2 \\ a_3x_1+a_4x_3 & a_3x_2+a_4x_4\end{pmatrix}=\begin{pmatrix}x_1b_1 & x_1b_2+x_2b_4 \\ x_3b_1 & x_3b_2+x_4b_4\end{pmatrix} \\ \Rightarrow \left\{\begin{matrix} a_1x_1=x_1b_1 \\ a_1x_2=x_1b_2+x_2b_4 \\ a_3x_1+a_4x_3=x_3b_1 \\ a_3x_2+a_4x_4=x_3b_2+x_4b_4 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} (a_1-b_1)x_1=0 \\ (a_1-b_4)x_2=x_1b_2 \\ a_3x_1=x_3(b_1-a_4) \\ a_3x_2=x_3b_2+x_4(b_4-a_4) \end{matrix}\right.$

Για την κετεύθυνση $\Leftarrow$ έχουμε ότι $\{a_1, a_4\}\cap \{b_1, b_4\}=\emptyset$ , άρα έχουμε τα εξής:
Αφού $a_1\neq b_1$ πρέπει $(a_1-b_1)x_1=0 \Rightarrow x_1=0$ .
Από την δεύτερη εξίσωση έχουμε ότι $(a_1-b_4)x_2=x_1b_2\Rightarrow (a_1-b_4)x_2=0$ , αφού $a_1\neq b_4$ έπεται ότι x_2=0

.
Από την τρίτη εξίσωση έχουμε ότι $a_3x_1=x_3(b_1-a_4)\Rightarrow x_3(b_1-a_4)=0$ , αφού $b_1\neq a_4$ έπεται ότι x_3=0

.
Από την τελευταία εξίσωση έχουμε ότι $a_3x_2=x_3b_2+x_4(b_4-a_4)\Rightarrow 0=x_4(b_4-a_4)$ , αφού $b_4\neq a_4$ έπεται ότι x_4=0

.

Οπότε ο πίνακας

είναι ο μηδενικός πίνακας, και άρα $U=\{0\}$ , σωστά;

Πώς μπορούμε να δείξουμε την άλλη κατεύθυνση;
Όταν έχουμε τον μηδενικό πίνακα, δεν ισχύει για κάθε

και

;

dement · #2

Ποια ιδιότητα έχει το σύστημα εξισώσεων που έφτιαξες; Ποια είναι η αναγκαία και ικανή συνθήκη για να έχει μοναδική λύση;

Mathletic · #3

dement έγραψε:Ποια ιδιότητα έχει το σύστημα εξισώσεων που έφτιαξες; Ποια είναι η αναγκαία και ικανή συνθήκη για να έχει μοναδική λύση;

Έχουμε το σύστημα
$\left\{\begin{matrix} (a_1-b_1)x_1=0 \\ b_2x_1-(a_1-b_4)x_2=0 \\ a_3x_1-(b_1-a_4)x_3=0 \\ a_3x_2-b_2x_3-(b_4-a_4)x_4 =0 \end{matrix}\right.\\ \Rightarrow \begin{pmatrix}(a_1-b_1) & 0 & 0 & 0 \\ b_2 & -(a_1-b_1) & 0 & 0 \\ a_3 & 0 & -(b_1-a_4) & 0 \\ 0 & a_3 & -b_2 & -(b_4-a_4)\end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4\end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0\end{pmatrix}$

Το σύστημα έχει μοναδική λύση, την μηδενική, αν και μόνο αν rank[A] = 4

.

Οπότε στην διαγώνιο τα στοιχεία πρέπει να είναι μη-μηδενικά, μετά την απαλοιφή Gauss, σωστά;

dement · #4

Διόρθωσε ένα τυπογραφικό στο στοιχείο (2,2)

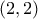του πίνακα των συντελεστών και είσαι έτοιμος.

Mathletic · #5

Α ναι. Ευχαριστώ πολύ!!

Δεν ισχύει για κάθε Α και Β;

Δεν ισχύει για κάθε Α και Β;

Re: Δεν ισχύει για κάθε Α και Β;

Re: Δεν ισχύει για κάθε Α και Β;

Re: Δεν ισχύει για κάθε Α και Β;

Re: Δεν ισχύει για κάθε Α και Β;

Μέλη σε σύνδεση