socrates έγραψε:50)

Η παραπάνω εξίσωση μετασχηματίζεται στην...
![2(x-y)[(x+y)(x-y)+2]=[(x+y)^2+(x-y)^2][(2k-(x+y)] 2(x-y)[(x+y)(x-y)+2]=[(x+y)^2+(x-y)^2][(2k-(x+y)]](/forum/ext/geomar/texintegr/latexrender/pictures/77077a3362f86d9511a7af28449cb46a.png)
 ,
,  ,
,  oπότε
oπότε 
 oπότε
oπότε  ή
ή  και τα πράγματα είναι απλά....
και τα πράγματα είναι απλά....Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
socrates έγραψε:50)

![2(x-y)[(x+y)(x-y)+2]=[(x+y)^2+(x-y)^2][(2k-(x+y)] 2(x-y)[(x+y)(x-y)+2]=[(x+y)^2+(x-y)^2][(2k-(x+y)]](/forum/ext/geomar/texintegr/latexrender/pictures/77077a3362f86d9511a7af28449cb46a.png)
 ,
,  ,
,  oπότε
oπότε 
 oπότε
oπότε  ή
ή  και τα πράγματα είναι απλά....
και τα πράγματα είναι απλά.... στους ακεραίους.
στους ακεραίους.Γεια σου Βασίλη!mathxl έγραψε:51)
Να λυθεί η εξίσωσηστους ακεραίους.


 .
. είναι
είναι 


Επαναφορά. (Το θέμα έχει δυσκολίες . Ούτε και στο site που το βρήκε υπήρχε σωστή λύση.)socrates έγραψε:
46)πρώτος
Αρχιμήδης 6 έγραψε:Επαναφορά. (Το θέμα έχει δυσκολίες . Ούτε και στο site που το βρήκε υπήρχε σωστή λύση.)socrates έγραψε:
46)πρώτος

 θα πας σε
θα πας σε  για να αποδείξεις ότι
για να αποδείξεις ότι  οπότε και
οπότε και 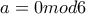 .
. και θα διαπιστώσεις εκεί την αδυναμία της εξίσωσης.
και θα διαπιστώσεις εκεί την αδυναμία της εξίσωσης.
 όπου
όπου  άρα έχει λύσεις μόνο για
άρα έχει λύσεις μόνο για  ....
....socrates έγραψε:Η 46 δε γνωρίζω αν έχει λύση.Την είδα εδώ, όμως δεν υπάρχει πλήρης λύση..
Γιαsocrates έγραψε: 46)πρώτος
 ,
,  η εξίσωση δεν έχει λύσεις άρα ψάχνω
η εξίσωση δεν έχει λύσεις άρα ψάχνω  .
. (1)
(1) Από θεώρημα Fermat-Euler
Από θεώρημα Fermat-Euler  oπότε
oπότε 

 ισχύει
ισχύει  ,
,  (2)
(2)
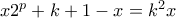
 (3)
(3) οι ρίζες του τότε θα πρέπει
οι ρίζες του τότε θα πρέπει 
 η
η  Για
Για  η (2) θα γίνει
η (2) θα γίνει  και είναι αδύνατον αν δεχθώ ότι
και είναι αδύνατον αν δεχθώ ότι  θετικός.
θετικός. η (2) θα γίνει
η (2) θα γίνει  και μετά από (1) ...
και μετά από (1) ...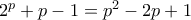
 δεν έχει λύσεις γιατί
δεν έχει λύσεις γιατί  περιττός και στο πρώτο μέλος έχουμε δύναμη του
περιττός και στο πρώτο μέλος έχουμε δύναμη του  .
.
 ισχύει
ισχύει 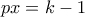 ,
,  (4)
(4)

 (5)
(5) οι ρίζες του τότε θα πρέπει
οι ρίζες του τότε θα πρέπει 
 η
η 
 η (4) θα γίνει
η (4) θα γίνει 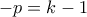 και είναι αδύνατον αν δεχθώ ότι
και είναι αδύνατον αν δεχθώ ότι  θετικός.
θετικός. η (4) θα γίνει
η (4) θα γίνει και μετά από (1) ...
και μετά από (1) ...
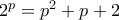 (6)
(6) πάμε για
πάμε για  Για
Για  η εξίσωση (6) επαληθεύεται το ίδιο και η αρχική εξίσωση και παίρνω το ζεύγος
η εξίσωση (6) επαληθεύεται το ίδιο και η αρχική εξίσωση και παίρνω το ζεύγος 
 αποδεικνύεται εύκολα με επαγωγή ότι
αποδεικνύεται εύκολα με επαγωγή ότι  οπότε η εξίσωση (6) δεν έχει λύσεις.
οπότε η εξίσωση (6) δεν έχει λύσεις.
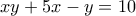 .
.
Μπορεί κάποιος να δώσει αναλυτική λύση; Γιατί είναι κάποια πράγματα που δεν τα έχω καταλάβει στην λύση του "Αρχιμήδης"Αρχιμήδης 6 έγραψε:
ή
&

Εύκολα βρίσκουμεκαι μένει να λυθεί η εξίσωση
άρα
διαιρεί το
κ.τ.λ
Μοναδικές λύσεις
Έχει κενά η λύση και σε ευχαριστώ.gauss1988 έγραψε:Μπορεί κάποιος να δώσει αναλυτική λύση; Γιατί είναι κάποια πράγματα που δεν τα έχω καταλάβει στην λύση του "Αρχιμήδης"Αρχιμήδης 6 έγραψε:
ή
&

Εύκολα βρίσκουμεκαι μένει να λυθεί η εξίσωση
άρα
διαιρεί το
κ.τ.λ
Μοναδικές λύσεις
Ευχαριστώ
 η
η  τότε θα πάρω τα ζεύγη
τότε θα πάρω τα ζεύγη 

 (1) και
(1) και  (2) για έναν πρώτο
(2) για έναν πρώτο  .
. (3)
(3) τότε
τότε  άρα
άρα  (4)
(4) αδύνατον οπότε
αδύνατον οπότε  Άρα έχεις να λύσεις το σύστημα
Άρα έχεις να λύσεις το σύστημα (5)
(5) , (6) (
, (6) (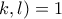
 (7)
(7)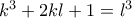
Συνεχίζοντας ακριβώς από εκεί που είχα μείνει...Αρχιμήδης 6 έγραψε:Έχει κενά η λύση και σε ευχαριστώ.gauss1988 έγραψε:Μπορεί κάποιος να δώσει αναλυτική λύση; Γιατί είναι κάποια πράγματα που δεν τα έχω καταλάβει στην λύση του "Αρχιμήδης"Αρχιμήδης 6 έγραψε:
ή
&

Εύκολα βρίσκουμεκαι μένει να λυθεί η εξίσωση
άρα
διαιρεί το
κ.τ.λ
Μοναδικές λύσεις
Ευχαριστώ
Δες μια προσέγγιση.
Ανη
τότε θα πάρω τα ζεύγη
Έστω(1) και
(2) για έναν πρώτο
.
Τότε από (1),(2)(3)
Αλλά αν πας στην αρχική εξίσωση αφούτότε
άρα
(4)
Από (3),(4) θα λάβειςαδύνατον οπότε
Άρα έχεις να λύσεις το σύστημα
(5)
, (6) (
(7)
Από (5),(6),(7) θα καταλήξεις στην παρακάτω εξίσωση.
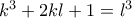
(Θα την συνεχίσω αργότερα.)
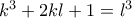 (8) με
(8) με  μη μηδενικοί.
μη μηδενικοί. (9) για
(9) για  ακέραιος.
ακέραιος.
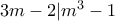 άρα
άρα 
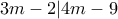


 και από τις (8),(9) θα καταλήξεις στα ζεύγη
και από τις (8),(9) θα καταλήξεις στα ζεύγη 
 πάλι από τις (8),(9) δεν θα πάρουμε λύση.
πάλι από τις (8),(9) δεν θα πάρουμε λύση.
Και μία δεύτερη λύση ως προς την παραγοντοποίησηxr.tsif έγραψε:ΑΣΚΗΣΗ 52
άντε και μία εύκολη
Να λύσετε στο σύνολο των ακεραίων την εξισωση:.
 .
.Ευχαριστώ. Νομίζω ότι κατάλαβα τώρα. Ήταν μια θαυμάσια εξίσωση και έγραψες μια θαυμάσια λύση!Αρχιμήδης 6 έγραψε:Συνεχίζοντας ακριβώς από εκεί που είχα μείνει...Αρχιμήδης 6 έγραψε:Έχει κενά η λύση και σε ευχαριστώ.gauss1988 έγραψε:Μπορεί κάποιος να δώσει αναλυτική λύση; Γιατί είναι κάποια πράγματα που δεν τα έχω καταλάβει στην λύση του "Αρχιμήδης"Αρχιμήδης 6 έγραψε:
ή
&

Εύκολα βρίσκουμεκαι μένει να λυθεί η εξίσωση
άρα
διαιρεί το
κ.τ.λ
Μοναδικές λύσεις
Ευχαριστώ
Δες μια προσέγγιση.
Ανη
τότε θα πάρω τα ζεύγη
Έστω(1) και
(2) για έναν πρώτο
.
Τότε από (1),(2)(3)
Αλλά αν πας στην αρχική εξίσωση αφούτότε
άρα
(4)
Από (3),(4) θα λάβειςαδύνατον οπότε
Άρα έχεις να λύσεις το σύστημα
(5)
, (6) (
(7)
Από (5),(6),(7) θα καταλήξεις στην παρακάτω εξίσωση.
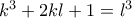
(Θα την συνεχίσω αργότερα.)
(8) με
μη μηδενικοί.
Έστω ότι(9) για
ακέραιος.
Αντικαθιστώντας στην εξίσωση και με πράξεις θα καταλήξεις στην
Άραάρα
Οπότε θα δεχτούμε ότι
Γιακαι από τις (8),(9) θα καταλήξεις στα ζεύγη
Γιαπάλι από τις (8),(9) δεν θα πάρουμε λύση.
Μοναδικές λύσεις τα ζεύγη

socrates έγραψε:10)
12)
17)
19)
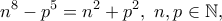
πρώτος.
20)
(θετικοί) πρώτοι
34)πρώτοι
35)
47)
Αυτή γράφεταιsocrates έγραψε:Άλυτες παραμένουν οι επόμενες:
socrates έγραψε: 12)
 .
. , και πρέπει η διακρίνουσα να είναι τέλειο τετράγωνο, δηλαδή
, και πρέπει η διακρίνουσα να είναι τέλειο τετράγωνο, δηλαδή  (*).
(*). πρέπει να είναι και οι δύο άρτιοι.
πρέπει να είναι και οι δύο άρτιοι. , και τελικά
, και τελικά  .
.Αν τουλάχιστον ένας εκ τωνsocrates έγραψε: 20)
(θετικοί) πρώτοι
 είναι
είναι  , τότε εύκολα παίρνουμε τις λύσεις
, τότε εύκολα παίρνουμε τις λύσεις  .
. . Τότε, προφανώς δεν γίνεται
. Τότε, προφανώς δεν γίνεται  , οπότε
, οπότε  , και άρα από το Fermat's Little Theorem ισχύει
, και άρα από το Fermat's Little Theorem ισχύει  και
και  .
.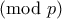 και
και  , προκύπτει
, προκύπτει  και
και  .
. , με
, με  . Αν
. Αν  , τότε
, τότε  (αφού
(αφού  ), άτοπο.
), άτοπο. .
. , τότε
, τότε  , οπότε
, οπότε  ή
ή  , και τα δύο απορρίπτονται.
, και τα δύο απορρίπτονται. , τότε
, τότε  , οπότε
, οπότε  .
. , ισχύει
, ισχύει  .
. με
με 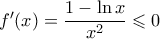 , για
, για  .
. είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  και συνεπώς
και συνεπώς  , και η απόδειξη του Λήμματος ολοκληρώθηκε .
, και η απόδειξη του Λήμματος ολοκληρώθηκε . , είναι
, είναι  , άρα από το Λήμμα
, άρα από το Λήμμα 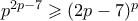 , οπότε
, οπότε  , άτοπο για
, άτοπο για  .
.
Προφανώς,
 ή
ή  (αν
(αν  ,
,  , άτοπο).
, άτοπο). , τότε
, τότε  , με
, με  φυσικό, οπότε
φυσικό, οπότε 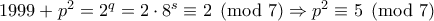 , άτοπο αφού το
, άτοπο αφού το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  .
. , τότε
, τότε  , οπότε
, οπότε  .
. .
.Αν
 άρτιος, έστω
άρτιος, έστω  και
και  , τότε
, τότε  , άτοπο αφού το
, άτοπο αφού το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο 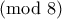 .
. είναι περιττός. Αν
είναι περιττός. Αν  , τότε ο
, τότε ο  έχει έναν πρώτο διαιρέτη
έχει έναν πρώτο διαιρέτη  ώστε
ώστε  . Οπότε,
. Οπότε,  , και άρα από γνωστό Λήμμα,
, και άρα από γνωστό Λήμμα,  , άτοπο αφού ο
, άτοπο αφού ο  είναι περιττός.
είναι περιττός. .
. .
. , άρα υπάρχει πρώτος
, άρα υπάρχει πρώτος 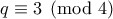 , ώστε
, ώστε 

 ,επομένως
,επομένως  .
. . Τότε, πρέπει
. Τότε, πρέπει  οπότε
οπότε  .
. , και πρέπει
, και πρέπει  .
. , άρα έχει έναν πρώτο διαιρέτη
, άρα έχει έναν πρώτο διαιρέτη  , οπότε
, οπότε  , άτοπο αφού
, άτοπο αφού  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης