 , με
, με  να είναι θετικοί ακέραιοι, υπάρχουν ώστε
να είναι θετικοί ακέραιοι, υπάρχουν ώστε  ;
;Φιλικά,
Αχιλλέας
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
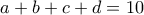 .
.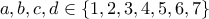 .
. Αν έστω και ένας εκ των όρων ισούται με
Αν έστω και ένας εκ των όρων ισούται με 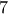 τότε οι υπόλοιποι τρεις θα είναι οπωσδήποτε ίσοι με τη μονάδα κι έτσι έχουμε
τότε οι υπόλοιποι τρεις θα είναι οπωσδήποτε ίσοι με τη μονάδα κι έτσι έχουμε  τέτοια πολυώνυμα.
τέτοια πολυώνυμα. Αν ο μεγαλύτερος συντελεστής είναι
Αν ο μεγαλύτερος συντελεστής είναι  τότε οι άλλοι τρεις θα είναι οι
τότε οι άλλοι τρεις θα είναι οι 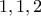 .Σύμφωνα με τον τύπο των αναγραμματισμών παίρνουμε
.Σύμφωνα με τον τύπο των αναγραμματισμών παίρνουμε  τέτοια πολυώνυμα.
τέτοια πολυώνυμα. Αν ο μεγαλύτερος συντελεστής είναι
Αν ο μεγαλύτερος συντελεστής είναι  οι πιθανοί συνδυασμοί για τους άλλους τρεις είναι
οι πιθανοί συνδυασμοί για τους άλλους τρεις είναι 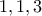 και
και 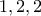 .Οπότε συνολικά παίρνουμε
.Οπότε συνολικά παίρνουμε 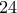 πολυώνυμα.
πολυώνυμα. Αν ο μεγαλύτερος συντελεστής είναι
Αν ο μεγαλύτερος συντελεστής είναι  έχουμε
έχουμε  πιθανούς συνδυασμούς.Τους
πιθανούς συνδυασμούς.Τους 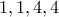 -
- 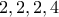 -
-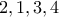 οι οποίοι μας δίνουν
οι οποίοι μας δίνουν  πολυώνυμα.
πολυώνυμα. Αν ο μεγαλύτερος συντελεστής είναι
Αν ο μεγαλύτερος συντελεστής είναι  υπάρχουν δύο πιθανοί συνδυασμοί,ο
υπάρχουν δύο πιθανοί συνδυασμοί,ο 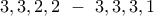 που μας δίνουν
που μας δίνουν  πολυώνυμα.
πολυώνυμα. .
. πολυώνυμα ικανοποιούν τις συνθήκες του προβλήματος.
πολυώνυμα ικανοποιούν τις συνθήκες του προβλήματος. , με
, με  να είναι θετικοί ακέραιοι, υπάρχουν ώστε
να είναι θετικοί ακέραιοι, υπάρχουν ώστε  όπου
όπου  ;
;
 θετικοί φυσικοί.
θετικοί φυσικοί.

 φυσικοί.
φυσικοί.


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης