Να αποδείξετε ότι η εξίσωση

ορίζει στον χώρο ομοέστιες επιφάνειες δεύτερης τάξης, οι οποίες αποτελούν τριπλά ορθογώνιο σύστημα επιφανειών.
Συντονιστής: matha

 , έχουμε
, έχουμε  ή
ή  .
. .
. είναι και οι τρεις θετικοί.
είναι και οι τρεις θετικοί. , δηλ.
, δηλ.  η παραπάνω εξίσωση παριστάνει σφαίρα με κέντρο Ο(0,0,0) και ακτίνα
η παραπάνω εξίσωση παριστάνει σφαίρα με κέντρο Ο(0,0,0) και ακτίνα  .
. ή
ή  ή
ή  η παραπάνω εξίσωση παριστάνει ελλειψοειδές με κέντρο Ο(0,0,0), άξονες πάνω στους άξονες x΄x, y΄y και z΄z και μήκη αξόνων
η παραπάνω εξίσωση παριστάνει ελλειψοειδές με κέντρο Ο(0,0,0), άξονες πάνω στους άξονες x΄x, y΄y και z΄z και μήκη αξόνων  ,
,  και
και  αντίστοιχα. Ειδικά αν
αντίστοιχα. Ειδικά αν  ή
ή  ή
ή  το ελλειψοειδές είναι εκ περιστροφής με άξονα περιστροφής τον z΄z ή τον x΄x ή τον y΄y αντίστοιχα.
το ελλειψοειδές είναι εκ περιστροφής με άξονα περιστροφής τον z΄z ή τον x΄x ή τον y΄y αντίστοιχα. , δηλ.
, δηλ.  , τότε η τομή του παραπάνω ελλειψοειδούς με το επίπεδο z=0 είναι έλλειψη με εστίες
, τότε η τομή του παραπάνω ελλειψοειδούς με το επίπεδο z=0 είναι έλλειψη με εστίες  ,
,  , όπου
, όπου  δηλ.
δηλ.  , η τομή του παραπάνω ελλειψοειδούς με το επίπεδο y=0 είναι έλλειψη με εστίες
, η τομή του παραπάνω ελλειψοειδούς με το επίπεδο y=0 είναι έλλειψη με εστίες  ,
,  , όπου
, όπου  δηλ.
δηλ.  , ενώ η τομή του παραπάνω ελλειψοειδούς με το επίπεδο x=0 είναι έλλειψη με εστίες
, ενώ η τομή του παραπάνω ελλειψοειδούς με το επίπεδο x=0 είναι έλλειψη με εστίες  ,
,  , όπου
, όπου  δηλ.
δηλ.  .
. είναι διαφορετική, τα συμπεράσματα είναι ανάλογα.
είναι διαφορετική, τα συμπεράσματα είναι ανάλογα. δύο είναι αρνητικοί και ένας θετικός.
δύο είναι αρνητικοί και ένας θετικός. και
και  και
και  . Τότε η παραπάνω εξίσωση παριστάνει δίχωνο υπερβολοειδές με κέντρο Ο(0,0,0) και άξονα τον z΄z. Ειδικά αν
. Τότε η παραπάνω εξίσωση παριστάνει δίχωνο υπερβολοειδές με κέντρο Ο(0,0,0) και άξονα τον z΄z. Ειδικά αν  το δίχωνο υπερβολοειδές είναι εκ περιστροφής με άξονα περιστροφής τον z΄z .
το δίχωνο υπερβολοειδές είναι εκ περιστροφής με άξονα περιστροφής τον z΄z . , οπότε
, οπότε  , η τομή του παραπάνω δίχωνου υπερβολοειδούς με το επίπεδο y=0 είναι υπερβολή με εστίες
, η τομή του παραπάνω δίχωνου υπερβολοειδούς με το επίπεδο y=0 είναι υπερβολή με εστίες  ,
,  , όπου
, όπου  δηλ.
δηλ.  , ενώ η τομή του παραπάνω δίχωνου υπερβολοειδούς με το επίπεδο x=0 είναι υπερβολή με εστίες
, ενώ η τομή του παραπάνω δίχωνου υπερβολοειδούς με το επίπεδο x=0 είναι υπερβολή με εστίες  ,
,  , όπου
, όπου  δηλ.
δηλ.  .
.  είναι διαφορετική, τα συμπεράσματα είναι ανάλογα.
είναι διαφορετική, τα συμπεράσματα είναι ανάλογα. .
. είναι και οι τρεις αρνητικοί.
είναι και οι τρεις αρνητικοί. δύο είναι θετικοί και ένας αρνητικός.
δύο είναι θετικοί και ένας αρνητικός. και
και  και
και  . Τότε η παραπάνω εξίσωση παριστάνει μονόχωνο υπερβολοειδές με κέντρο Ο(0,0,0), λαιμό πάνω στο επίπεδο xOy και άξονα τον z΄z. Ειδικά αν
. Τότε η παραπάνω εξίσωση παριστάνει μονόχωνο υπερβολοειδές με κέντρο Ο(0,0,0), λαιμό πάνω στο επίπεδο xOy και άξονα τον z΄z. Ειδικά αν  το μονόχωνο υπερβολοειδές είναι εκ περιστροφής με άξονα περιστροφής τον z΄z .
το μονόχωνο υπερβολοειδές είναι εκ περιστροφής με άξονα περιστροφής τον z΄z . , οπότε
, οπότε  , ο λαιμός του παραπάνω μονόχωνου υπερβολοειδούς είναι έλλειψη με εστίες
, ο λαιμός του παραπάνω μονόχωνου υπερβολοειδούς είναι έλλειψη με εστίες  ,
,  , όπου
, όπου  δηλ.
δηλ.  , η τομή του παραπάνω μονόχωνου υπερβολοειδούς με το επίπεδο y=0 είναι υπερβολή με εστίες
, η τομή του παραπάνω μονόχωνου υπερβολοειδούς με το επίπεδο y=0 είναι υπερβολή με εστίες  ,
,  , όπου
, όπου  δηλ.
δηλ.  , ενώ η τομή του παραπάνω μονόχωνου υπερβολοειδούς με το επίπεδο x=0 είναι υπερβολή με εστίες
, ενώ η τομή του παραπάνω μονόχωνου υπερβολοειδούς με το επίπεδο x=0 είναι υπερβολή με εστίες  ,
,  , όπου
, όπου 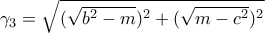 δηλ.
δηλ.  .
. είναι διαφορετική, τα συμπεράσματα είναι ανάλογα.
είναι διαφορετική, τα συμπεράσματα είναι ανάλογα. και
και  , η παραπάνω εξίσωση παριστάνει ελλειψοειδές, του οποίου οι τομές με τα συντεταγμένα επίπεδα είναι ελλείψεις με εστίες, που έχουν συντεταγμένες ανεξάρτητες από την τιμή της παραμέτρου m.
, η παραπάνω εξίσωση παριστάνει ελλειψοειδές, του οποίου οι τομές με τα συντεταγμένα επίπεδα είναι ελλείψεις με εστίες, που έχουν συντεταγμένες ανεξάρτητες από την τιμή της παραμέτρου m. και
και  και m μικρότερο από τα άλλα δύο στοιχεία του συνόλου
και m μικρότερο από τα άλλα δύο στοιχεία του συνόλου  , η παραπάνω εξίσωση παριστάνει μονόχωνο υπερβολοειδές, του οποίου οι τομές με τα συντεταγμένα επίπεδα είναι έλλειψη και υπερβολές με εστίες, που έχουν συντεταγμένες ανεξάρτητες από την τιμή της παραμέτρου m.
, η παραπάνω εξίσωση παριστάνει μονόχωνο υπερβολοειδές, του οποίου οι τομές με τα συντεταγμένα επίπεδα είναι έλλειψη και υπερβολές με εστίες, που έχουν συντεταγμένες ανεξάρτητες από την τιμή της παραμέτρου m. και m μεγαλύτερο από τα δύο στοιχεία του συνόλου
και m μεγαλύτερο από τα δύο στοιχεία του συνόλου  και
και  , η παραπάνω εξίσωση παριστάνει δίχωνο υπερβολοειδές, του οποίου οι τομές με τα συντεταγμένα επίπεδα είναι υπερβολές με εστίες, που έχουν συντεταγμένες ανεξάρτητες από την τιμή της παραμέτρου m.
, η παραπάνω εξίσωση παριστάνει δίχωνο υπερβολοειδές, του οποίου οι τομές με τα συντεταγμένα επίπεδα είναι υπερβολές με εστίες, που έχουν συντεταγμένες ανεξάρτητες από την τιμή της παραμέτρου m. και ας είναι
και ας είναι  τρεις τιμές της παραμέτρου m, ώστε
τρεις τιμές της παραμέτρου m, ώστε  και
και 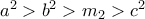 και
και  .
.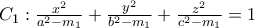 (ελλειψοειδές) και
(ελλειψοειδές) και  (μονόχωνο υπερβολοειδές)
(μονόχωνο υπερβολοειδές) (δίχωνο υπερβολοειδές)
(δίχωνο υπερβολοειδές)
 έχει λύση
έχει λύση 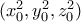 με
με  .
.
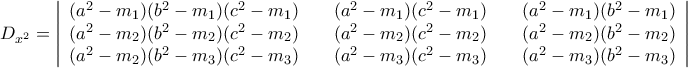






 ,
,  και (1)
και (1)  .
.  των
των 
 θα έχει εξίσωση
θα έχει εξίσωση  ,
, θα έχει εξίσωση
θα έχει εξίσωση  ,
, θα έχει εξίσωση
θα έχει εξίσωση  .
. είναι κάθετο στο επίπεδο
είναι κάθετο στο επίπεδο  , το διάνυσμα
, το διάνυσμα  είναι κάθετο στο επίπεδο
είναι κάθετο στο επίπεδο  , ενώ
, ενώ  είναι κάθετο στο επίπεδο
είναι κάθετο στο επίπεδο  .
.  , οπότε από τις σχέσεις (1) προκύπτει
, οπότε από τις σχέσεις (1) προκύπτει  .
.  τέμνονται κάθετα, επομένως και οι επιφάνειες
τέμνονται κάθετα, επομένως και οι επιφάνειες  τέμνονται κάθετα. Ομοίως προκύπτει ότι και οι επιφάνειες
τέμνονται κάθετα. Ομοίως προκύπτει ότι και οι επιφάνειες  τέμνονται κάθετα και οι επιφάνειες
τέμνονται κάθετα και οι επιφάνειες  τέμνονται κάθετα
τέμνονται κάθεταΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες