 μια κανονική επιφάνεια του
μια κανονική επιφάνεια του  . Να αποδειχθεί ότι αν όλα τα εφαπτόμενα επίπεδα της
. Να αποδειχθεί ότι αν όλα τα εφαπτόμενα επίπεδα της  διέρχονται από την αρχή των αξόνων, τότε η καμπυλότητα Gauss
διέρχονται από την αρχή των αξόνων, τότε η καμπυλότητα Gauss  της
της  είναι παντού μηδενική.
είναι παντού μηδενική.Συντονιστής: matha
 μια κανονική επιφάνεια του
μια κανονική επιφάνεια του  . Να αποδειχθεί ότι αν όλα τα εφαπτόμενα επίπεδα της
. Να αποδειχθεί ότι αν όλα τα εφαπτόμενα επίπεδα της  διέρχονται από την αρχή των αξόνων, τότε η καμπυλότητα Gauss
διέρχονται από την αρχή των αξόνων, τότε η καμπυλότητα Gauss  της
της  είναι παντού μηδενική.
είναι παντού μηδενική.
 η τοπική παράσταση της.
η τοπική παράσταση της.
 το κάθετο διάνυσμα και
το κάθετο διάνυσμα και 
 πέρνουμαι
πέρνουμαι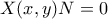
 είναι γραμμικός συνδιασμός των
είναι γραμμικός συνδιασμός των 
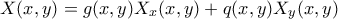

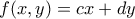
 που δίνει το ζητούμενο.
που δίνει το ζητούμενο. που δεν είναι η αρχή των αξόνων με
που δεν είναι η αρχή των αξόνων με  . Έστω
. Έστω  σύστημα συντεταγμένων γύρω από το
σύστημα συντεταγμένων γύρω από το  . Επειδή το εφαπτόμενο επίπεδο
. Επειδή το εφαπτόμενο επίπεδο 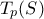 διέρχεται από την αρχή των αξόνων, έπεται ότι
διέρχεται από την αρχή των αξόνων, έπεται ότι  , δηλαδή
, δηλαδή  .
. 
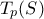 το σύνολο
το σύνολο  , προκύπτουν
, προκύπτουν 
 ,
,  είναι γραμμικώς ανεξάρτητα. Αλλά τότε, από την καθετότητα του
είναι γραμμικώς ανεξάρτητα. Αλλά τότε, από την καθετότητα του  με τα
με τα  ,
,  , προκύπτει ότι
, προκύπτει ότι  . Άτοπο. Κι αυτό γιατί θεωρήσαμε
. Άτοπο. Κι αυτό γιατί θεωρήσαμε  . Άρα σε κάθε σημείο
. Άρα σε κάθε σημείο  ισχύει
ισχύει  .
.
 , κλπ*)^ τέμνοντας τώρα την δοθείσα επιφάνεια με κάθε επίπεδο κάθετο στο επίπεδο
, κλπ*)^ τέμνοντας τώρα την δοθείσα επιφάνεια με κάθε επίπεδο κάθετο στο επίπεδο  που περιέχει τον άξονα των
που περιέχει τον άξονα των  λαμβάνουμε, σε κάθε ένα από τα κάθετα επίπεδα, καμπύλη με την ιδιότητα του λήμματος, άρα ευθεία γραμμή.
λαμβάνουμε, σε κάθε ένα από τα κάθετα επίπεδα, καμπύλη με την ιδιότητα του λήμματος, άρα ευθεία γραμμή. (στο οποίο η εφαπτόμενη διέρχεται από την αρχή των αξόνων) ... τότε αν είναι τοπικά κυρτή (και πάνω από την εφαπτόμενη στο
(στο οποίο η εφαπτόμενη διέρχεται από την αρχή των αξόνων) ... τότε αν είναι τοπικά κυρτή (και πάνω από την εφαπτόμενη στο  ) οι εφαπτόμενες σε σημεία αριστερά του
) οι εφαπτόμενες σε σημεία αριστερά του  τέμνουν τον άξονα των
τέμνουν τον άξονα των  πάνω από το
πάνω από το  και οι εφαπτόμενες σε σημεία δεξιά του
και οι εφαπτόμενες σε σημεία δεξιά του  τέμνουν τον άξονα των
τέμνουν τον άξονα των  κάτω από το
κάτω από το  , ενώ αν είναι τοπικά κοίλη (και κάτω από την εφαπτόμενη στο
, ενώ αν είναι τοπικά κοίλη (και κάτω από την εφαπτόμενη στο  ) τότε συμβαίνουν ακριβώς τα αντίθετα. (Τώρα αν η κυρτότητα/κοιλότητα μεταβάλλεται συνεχώς γύρω από το
) τότε συμβαίνουν ακριβώς τα αντίθετα. (Τώρα αν η κυρτότητα/κοιλότητα μεταβάλλεται συνεχώς γύρω από το  ... δεν βλέπω τρόπο διαφυγής...)
... δεν βλέπω τρόπο διαφυγής...)Μπορεί να γίνει κάτι καλύτερο (πέρα από επίλυση της απλής διαφορικής εξίσωσηςgbaloglou έγραψε: *ας το δούμε αυτό (το δισδιάστατο λήμμα) και πιο εποπτικά (αλλά όχι αυστηρά): αν η κλίση της καμπύλης αλλάζει γύρω από το σημείο επαφής(στο οποίο η εφαπτόμενη διέρχεται από την αρχή των αξόνων) ... τότε αν είναι τοπικά κυρτή (και πάνω από την εφαπτόμενη στο
) οι εφαπτόμενες σε σημεία αριστερά του
τέμνουν τον άξονα των
πάνω από το
και οι εφαπτόμενες σε σημεία δεξιά του
τέμνουν τον άξονα των
κάτω από το
, ενώ αν είναι τοπικά κοίλη (και κάτω από την εφαπτόμενη στο
) τότε συμβαίνουν ακριβώς τα αντίθετα. (Τώρα αν η κυρτότητα/κοιλότητα μεταβάλλεται συνεχώς γύρω από το
... δεν βλέπω τρόπο διαφυγής...)
 , που ήδη ανέφερα);
, που ήδη ανέφερα);



 δηλαδή
δηλαδή 

 δηλαδή
δηλαδή 

 αυθαίρετη ομαλή συνάρτηση.
αυθαίρετη ομαλή συνάρτηση. =0
=0  υποθέτοντας οτι
υποθέτοντας οτι 
 οπου
οπου  συνάρτηση
συνάρτηση 
 τότε η καμπυλότητα Gauss είναι 0 αν και μόνο αν
τότε η καμπυλότητα Gauss είναι 0 αν και μόνο αν 
 ικανοποιεί την τελευταία .
ικανοποιεί την τελευταία . κανονική παραμέτριση της επιφάνειας τοπικά.
κανονική παραμέτριση της επιφάνειας τοπικά. τα θεμελειώδη μεγέθη της πρώτης και δεύτερης μορφής
τα θεμελειώδη μεγέθη της πρώτης και δεύτερης μορφής 

 και για τα διανύσματα έχουμε μικτό γινόμενο.
και για τα διανύσματα έχουμε μικτό γινόμενο.
 παίρνουμε οτι
παίρνουμε οτι
 ώστε να έχουμε μικτό γινόμενο
ώστε να έχουμε μικτό γινόμενο


 έχει μη μηδενικές λύσεις
έχει μη μηδενικές λύσεις .Αρα
.Αρα 
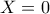 αυτό θα συμβαίνει το πολύ σε ένα σημείο.
αυτό θα συμβαίνει το πολύ σε ένα σημείο. .
.

 παίρνουμε
παίρνουμε



 έχει μη μηδενικές λύσεις εκτός αν
έχει μη μηδενικές λύσεις εκτός αν 
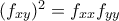 που δίνει καμπυλότητα Gauss 0.
που δίνει καμπυλότητα Gauss 0.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης