 λέγεται γεωδαισιακός, αν για κάθε
λέγεται γεωδαισιακός, αν για κάθε  υπάρχουν
υπάρχουν και απεικόνιση
και απεικόνιση ![\displaystyle{\gamma:\left[0,d\right]\to X} \displaystyle{\gamma:\left[0,d\right]\to X}](/forum/ext/geomar/texintegr/latexrender/pictures/4cd4229a210057ab1ce461d837574965.png) με
με 
και
![\displaystyle{\rho(\gamma(t),\gamma(t'))=|t-t'|\,,\forall\,t\,,t'\in \left[0,d\right]} \displaystyle{\rho(\gamma(t),\gamma(t'))=|t-t'|\,,\forall\,t\,,t'\in \left[0,d\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/4c0df2ffb0a88bc6f983a60ebed7e2ba.png) .
.Να αποδείξετε ότι το
 με την επαγόμενη μετρική του
με την επαγόμενη μετρική του 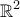
δεν είναι γεωδαισιακός μετρικός χώρος.
Συντονιστής: matha
 λέγεται γεωδαισιακός, αν για κάθε
λέγεται γεωδαισιακός, αν για κάθε  υπάρχουν
υπάρχουν και απεικόνιση
και απεικόνιση ![\displaystyle{\gamma:\left[0,d\right]\to X} \displaystyle{\gamma:\left[0,d\right]\to X}](/forum/ext/geomar/texintegr/latexrender/pictures/4cd4229a210057ab1ce461d837574965.png) με
με 
![\displaystyle{\rho(\gamma(t),\gamma(t'))=|t-t'|\,,\forall\,t\,,t'\in \left[0,d\right]} \displaystyle{\rho(\gamma(t),\gamma(t'))=|t-t'|\,,\forall\,t\,,t'\in \left[0,d\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/4c0df2ffb0a88bc6f983a60ebed7e2ba.png) .
. με την επαγόμενη μετρική του
με την επαγόμενη μετρική του 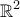
 . Τότε, για γεωδαισιακή καμπύλη
. Τότε, για γεωδαισιακή καμπύλη  , ισχύει
, ισχύει  . Έτσι, στην περίπτωση των Ευκλείδειων χώρων, το
. Έτσι, στην περίπτωση των Ευκλείδειων χώρων, το  πρέπει να βρίσκεται ανάμεσα στα
πρέπει να βρίσκεται ανάμεσα στα  και η καμπύλη πρέπει να είναι ευθεία. Kάθε ζεύγος σημείων
και η καμπύλη πρέπει να είναι ευθεία. Kάθε ζεύγος σημείων  πρέπει λοιπόν να συνδέεται με ευθύγραμμο τμήμα, κάθε σημείο του οποίου ανήκει στο χώρο.
πρέπει λοιπόν να συνδέεται με ευθύγραμμο τμήμα, κάθε σημείο του οποίου ανήκει στο χώρο. προφανώς δεν πληρούν τη συνθήκη (αφού το
προφανώς δεν πληρούν τη συνθήκη (αφού το  δεν ανήκει στο χώρο) και ο χώρος δεν είναι γεωδαισιακός.
δεν ανήκει στο χώρο) και ο χώρος δεν είναι γεωδαισιακός.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες