 με
με 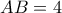 και
και 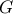 το βαρύκεντρο αυτού.
το βαρύκεντρο αυτού. Μεταβλητό σημείο
 κινείται στην περίμετρο του τριγώνου αυτού και για το
κινείται στην περίμετρο του τριγώνου αυτού και για το τρίγωνο
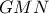 ισχύει:
ισχύει: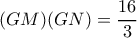
και
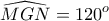 .
.Να βρεθεί ο γ. τόπος του σημείου
 .
. Συντονιστής: matha
 με
με 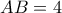 και
και 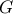 το βαρύκεντρο αυτού.
το βαρύκεντρο αυτού.  κινείται στην περίμετρο του τριγώνου αυτού και για το
κινείται στην περίμετρο του τριγώνου αυτού και για το 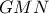 ισχύει:
ισχύει: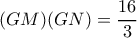
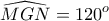 .
. .
. 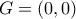 ,
, 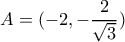 ,
, 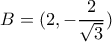 ,
, 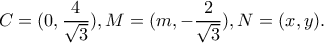
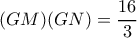 λαμβάνουμε
λαμβάνουμε 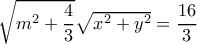 .
.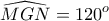 λαμβάνουμε
λαμβάνουμε 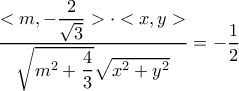 .
.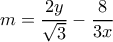 , και αντικαθιστώντας στην πρώτη ισότητα παραπάνω λαμβάνουμε
, και αντικαθιστώντας στην πρώτη ισότητα παραπάνω λαμβάνουμε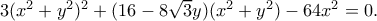
 όταν το
όταν το  κινείται επί της πλευράς/ευθείας
κινείται επί της πλευράς/ευθείας  , η συμμετρία περί το μέσον της
, η συμμετρία περί το μέσον της  είναι προφανής, η παρουσία του όρου
είναι προφανής, η παρουσία του όρου  θυμίζει κύκλο, άρα είναι πολύ λογικό να αναζητήσουμε συμμετρικά τόξα κύκλου στην παραπάνω εξίσωση ... και συνεπώς να (προσπαθήσουμε να) την παραγοντοποιήσουμε:
θυμίζει κύκλο, άρα είναι πολύ λογικό να αναζητήσουμε συμμετρικά τόξα κύκλου στην παραπάνω εξίσωση ... και συνεπώς να (προσπαθήσουμε να) την παραγοντοποιήσουμε: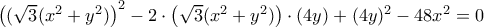
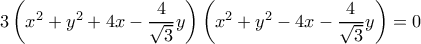
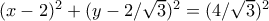 και
και 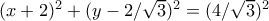 , βλέπετε και συνημμένο.
, βλέπετε και συνημμένο.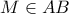 . Εύκολα διαπιστώνουμε ότι τα 'εξωτερικά ημιτόξα'
. Εύκολα διαπιστώνουμε ότι τα 'εξωτερικά ημιτόξα' 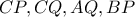 αντιστοιχούν στις 2 x 2 = 4 δυνατές περιπτώσεις (θετική
αντιστοιχούν στις 2 x 2 = 4 δυνατές περιπτώσεις (θετική  ή αρνητική
ή αρνητική  γωνία
γωνία 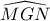 , δεξιό ήμισυ
, δεξιό ήμισυ  ή αριστερό ήμισυ
ή αριστερό ήμισυ  πλευράς
πλευράς  ).
). 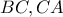 συμπεραίνουμε ότι ο ζητούμενος γεωμετρικός τόπος αποτελείται από τρία τόξα κύκλων εξωτερικά του δοθέντος ισοπλεύρου τριγώνου
συμπεραίνουμε ότι ο ζητούμενος γεωμετρικός τόπος αποτελείται από τρία τόξα κύκλων εξωτερικά του δοθέντος ισοπλεύρου τριγώνου  . Τα κέντρα αυτών των κύκλων είναι τα συμμετρικά του βαρύκεντρου
. Τα κέντρα αυτών των κύκλων είναι τα συμμετρικά του βαρύκεντρου  ως προς τις τρεις πλευρές, και η ακτίνα τους ίση προς
ως προς τις τρεις πλευρές, και η ακτίνα τους ίση προς 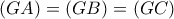 .
.Να σημειώσω ότι για να είμαστε εντάξει πρέπει να πούμε ότι
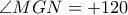
 σημείο
σημείο  ώστε να είναι
ώστε να είναι 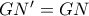 .
. βόσκει στην
βόσκει στην  το
το  βόσκει σε ένα τόξο κύκλου.
βόσκει σε ένα τόξο κύκλου. και γωνία
και γωνία 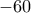 αυτού του τόξου βρίσκουμε ένα κομμάτι του τόπου.
αυτού του τόξου βρίσκουμε ένα κομμάτι του τόπου. και
και 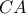 .
.Έστω ότι
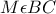 και
και 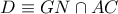 , τότε εύκολα προκύπτει η ισότητα των τριγώνων
, τότε εύκολα προκύπτει η ισότητα των τριγώνων 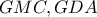 (Γ – Π – Γ ) οπότε
(Γ – Π – Γ ) οπότε 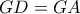 .
. 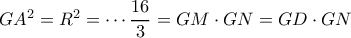 οπότε ο περίκυκλος του τριγώνου
οπότε ο περίκυκλος του τριγώνου 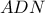 εφάπτεται της
εφάπτεται της 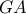 ,άρα
,άρα 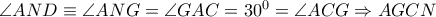 εγγράψιμο σε κύκλο και συνεπώς το
εγγράψιμο σε κύκλο και συνεπώς το  είναι σημείο του τόξου (που δεν περιέχει το
είναι σημείο του τόξου (που δεν περιέχει το  ) του περίκυκλου του τριγώνου
) του περίκυκλου του τριγώνου 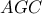 . Με όμοιο τρόπο προκύπτει ότι το
. Με όμοιο τρόπο προκύπτει ότι το  είναι σημείο των (αντιστοίχων) τόξων των περικύκλων των τριγώνων
είναι σημείο των (αντιστοίχων) τόξων των περικύκλων των τριγώνων 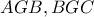 για θέση του
για θέση του  επί των
επί των 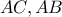 αντίστοιχα. Έτσι ο ζητούμενος γεωμετρικός τόπος είναι τα κόκκινα τρία τόξα. Εύκολα προκύπτει και το αντίστροφο …
αντίστοιχα. Έτσι ο ζητούμενος γεωμετρικός τόπος είναι τα κόκκινα τρία τόξα. Εύκολα προκύπτει και το αντίστροφο …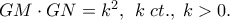
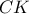 και την προβολή του
και την προβολή του  στην
στην 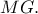 Αν
Αν  η τομή της
η τομή της 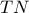 με την
με την 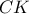 , τότε,
, τότε, 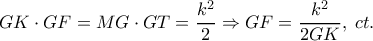
 λοιπόν είναι ένα σταθερό σημείο, οπότε το σημείο
λοιπόν είναι ένα σταθερό σημείο, οπότε το σημείο  θα κινείται σε σταθερό κύκλο κέντρου
θα κινείται σε σταθερό κύκλο κέντρου  που είναι το μέσο της διαμέτρου του
που είναι το μέσο της διαμέτρου του 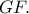 Θεωρούμε τώρα ορθογώνιο στο
Θεωρούμε τώρα ορθογώνιο στο  τρίγωνο
τρίγωνο 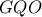 όμοιο προς το ορθογώνιο τρίγωνο
όμοιο προς το ορθογώνιο τρίγωνο 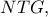 οπότε το τρίγωνο
οπότε το τρίγωνο 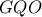 θα είναι σταθερό. Άμεσα παίρνουμε την ομοιότητα των τριγώνων
θα είναι σταθερό. Άμεσα παίρνουμε την ομοιότητα των τριγώνων 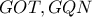 , από την οποία προκύπτει ότι το τρίγωνο
, από την οποία προκύπτει ότι το τρίγωνο 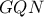 είναι ισοσκελές. Επομένως το σημείο
είναι ισοσκελές. Επομένως το σημείο  θα κινείται στον σταθερό κύκλο
θα κινείται στον σταθερό κύκλο 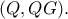 Εννοείται ότι το "σκηνικό" αυτό θα γίνει και για τις άλλες δύο πλευρές, ώστε να πάρουμε την ένωση.
Εννοείται ότι το "σκηνικό" αυτό θα γίνει και για τις άλλες δύο πλευρές, ώστε να πάρουμε την ένωση.
 Αν δεν έχουμε Κατασκευαστικό Γεωμετρικά προσδιορισμό, τότε, παραμένουμε στην απόδειξη της ύπαρξης.
Αν δεν έχουμε Κατασκευαστικό Γεωμετρικά προσδιορισμό, τότε, παραμένουμε στην απόδειξη της ύπαρξης.Αν και η παραπάνω αλγεβρική λύση μου (#2) ακολουθήθηκε και ξεπεράστηκε από γεωμετρικές προσεγγίσεις, θα ήθελα να δω -- στα πλαίσια της δικής μου προσέγγισης πάντοτε -- λίγο και το αντίστροφο, πως για παράδειγμα το κάθε σημείοgbaloglou έγραψε: ↑Πέμ Σεπ 17, 2020 9:54 pmΠροσέγγιση με απλή Αναλυτική Γεωμετρία (συν τύπο συνημιτόνου γωνίας διανυσμάτων μέσω μέτρων και εσωτερικού γινομένου):
Θέτουμε,
,
,
Από τηνλαμβάνουμε
.
Από τηνλαμβάνουμε
.
Από τις παραπάνω δύο ισότητες λαμβάνουμε, και αντικαθιστώντας στην πρώτη ισότητα παραπάνω λαμβάνουμε
Αυτό είναι και το κρίσιμο σημείο του προβλήματος: ως εδώ αναζητούμε ουσιαστικά τον γεωμετρικό τόπο τουόταν το
κινείται επί της πλευράς/ευθείας
, η συμμετρία περί το μέσον της
είναι προφανής, η παρουσία του όρου
θυμίζει κύκλο, άρα είναι πολύ λογικό να αναζητήσουμε συμμετρικά τόξα κύκλου στην παραπάνω εξίσωση ... και συνεπώς να (προσπαθήσουμε να) την παραγοντοποιήσουμε:
Προκύπτει ότι οι δύο κύκλοι είναι οικαι
, βλέπετε και συνημμένο.
Από εδώ και πέρα απαιτείται κάποια διερεύνηση, χωρίς να ξεχνάμε ότι έχουμε προς το παρόν μελετήσει μόνον την περίπτωση. Εύκολα διαπιστώνουμε ότι τα 'εξωτερικά ημιτόξα'
αντιστοιχούν στις 2 x 2 = 4 δυνατές περιπτώσεις (θετική
ή αρνητική
γωνία
, δεξιό ήμισυ
ή αριστερό ήμισυ
πλευράς
).
Ενεργώντας ανάλογα και για τις πλευρέςσυμπεραίνουμε ότι ο ζητούμενος γεωμετρικός τόπος αποτελείται από τρία τόξα κύκλων εξωτερικά του δοθέντος ισοπλεύρου τριγώνου
. Τα κέντρα αυτών των κύκλων είναι τα συμμετρικά του βαρύκεντρου
ως προς τις τρεις πλευρές, και η ακτίνα τους ίση προς
.
δορτσιος-17-9-20.png
 επί του τόξου
επί του τόξου  μας δίνει ένα σημείο
μας δίνει ένα σημείο 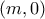 εντός του τμήματος
εντός του τμήματος  (ώστε να ισχύουν οι ζητούμενες παραπάνω ισότητες): εύκολα βλέπουμε ότι οφείλουμε, ξεκινώντας από τις
(ώστε να ισχύουν οι ζητούμενες παραπάνω ισότητες): εύκολα βλέπουμε ότι οφείλουμε, ξεκινώντας από τις 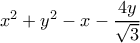 και
και  , να βρούμε
, να βρούμε  τέτοιο ώστε
τέτοιο ώστε 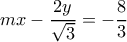 και
και 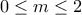 ^ οφείλουμε δηλαδή να δείξουμε ότι αν
^ οφείλουμε δηλαδή να δείξουμε ότι αν 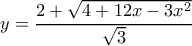 και
και  τότε ισχύει η
τότε ισχύει η 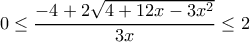 (εύκολο).
(εύκολο).Φίλοι μου γεια σας...
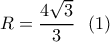
 .
. του τριγώνου αυτού επειδή δεν διέρχεται από το κέντρο αντιστροφής
του τριγώνου αυτού επειδή δεν διέρχεται από το κέντρο αντιστροφής 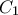 (με στικτή γραμμή), ο οποίος θα διέρχεται από το κέντρο της αντιστροφής
(με στικτή γραμμή), ο οποίος θα διέρχεται από το κέντρο της αντιστροφής 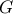
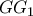 κάθετη στην
κάθετη στην  .
.  οποία είναι το τόξο:
οποία είναι το τόξο: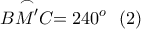
 του τριγώνου
του τριγώνου 
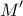 έχει εφαρμοστεί η στροφή με κέντρο στο σημείο
έχει εφαρμοστεί η στροφή με κέντρο στο σημείο  και με γωνία ίση με
και με γωνία ίση με 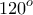
 του τριγώνου
του τριγώνου 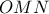 .
.  θα είναι η στροφή του τόξου
θα είναι η στροφή του τόξου 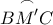 γύρω από το
γύρω από το  και κατά
και κατά 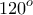 .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες