 , έχει κάθετες πλευρές
, έχει κάθετες πλευρές  και
και  . Η διχοτόμος
. Η διχοτόμοςτης
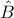 τέμνει το τεταρτοκύκλιο
τέμνει το τεταρτοκύκλιο  στο σημείο
στο σημείο  . Αν
. Αν  , υπολογίστε την
, υπολογίστε την  .
.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 , έχει κάθετες πλευρές
, έχει κάθετες πλευρές  και
και  . Η διχοτόμος
. Η διχοτόμος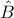 τέμνει το τεταρτοκύκλιο
τέμνει το τεταρτοκύκλιο  στο σημείο
στο σημείο  . Αν
. Αν  , υπολογίστε την
, υπολογίστε την  .
.Μάλλον έχει γίνει τυπογραφικό λάθος και είναι: Το ορθογώνιο τρίγωνοKARKAR έγραψε:Το ορθογώνιο τρίγωνο
 .
. .
.
 και
και 

 .
.Καλησπέρα!KARKAR έγραψε:Το ορθογώνιο τρίγωνο, έχει κάθετες πλευρές
και
. Η διχοτόμος
τηςτέμνει το τεταρτοκύκλιο
στο σημείο
. Αν
, υπολογίστε την
.



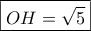


KαλησπέραKARKAR έγραψε:Το ορθογώνιο τρίγωνο, έχει κάθετες πλευρές
και
. Η διχοτόμος
τηςτέμνει το τεταρτοκύκλιο
στο σημείο
. Αν
, υπολογίστε την
.
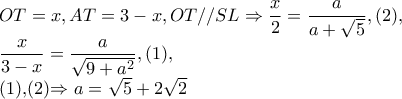
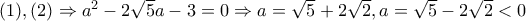
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης