 - μήκους
- μήκους  - ισοπλεύρου τριγώνου
- ισοπλεύρου τριγώνου  , κινείται σημείο
, κινείται σημείο 
Στην προέκταση της βάσης
 παίρνω σημείο
παίρνω σημείο  , ώστε
, ώστε 
α) Δείξτε ότι το μέσο
 του τμήματος
του τμήματος  , κινείται επί της
, κινείται επί της 
β) Αν
 οι προβολές των
οι προβολές των  στην
στην  , υπολογίστε το μέγιστο εμβαδόν του
, υπολογίστε το μέγιστο εμβαδόν του 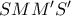
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 - μήκους
- μήκους  - ισοπλεύρου τριγώνου
- ισοπλεύρου τριγώνου  , κινείται σημείο
, κινείται σημείο 
 παίρνω σημείο
παίρνω σημείο  , ώστε
, ώστε 
 του τμήματος
του τμήματος  , κινείται επί της
, κινείται επί της 
 οι προβολές των
οι προβολές των  στην
στην  , υπολογίστε το μέγιστο εμβαδόν του
, υπολογίστε το μέγιστο εμβαδόν του 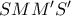

 φέρω // στην
φέρω // στην  που τέμνει την
που τέμνει την  στο
στο  . To
. To 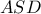 είναι ισόπλευρο οπότε
είναι ισόπλευρο οπότε 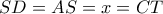 και συνεπώς το
και συνεπώς το  είναι παραλληλόγραμμο και οι διαγωνιές του διχοτομούνται. Αρα
είναι παραλληλόγραμμο και οι διαγωνιές του διχοτομούνται. Αρα  και
και 
 ......(1)
......(1) ......(2)
......(2) που έχει μέγιστο για
που έχει μέγιστο για  ,
, 
Καλησπέρα σε όλους!KARKAR έγραψε:Στην πλευρά- μήκους
- ισοπλεύρου τριγώνου
, κινείται σημείο

Στην προέκταση της βάσηςπαίρνω σημείο
, ώστε

α) Δείξτε ότι το μέσοτου τμήματος
, κινείται επί της

β) Ανοι προβολές των
στην
, υπολογίστε το μέγιστο εμβαδόν του
 είναι το σημείο τομής της
είναι το σημείο τομής της  με την
με την  τότε αρκεί το
τότε αρκεί το  να είναι μέσο του
να είναι μέσο του  .
. με διατέμνουσα την
με διατέμνουσα την  δίνει:
δίνει: . Έτσι, το ζητούμενο εδείχθη.
. Έτσι, το ζητούμενο εδείχθη. και
και  είναι όμοια. Αφού
είναι όμοια. Αφού  επειδή στο ορθογώνιο τρίγωνο
επειδή στο ορθογώνιο τρίγωνο  το
το  είναι μέσο
είναι μέσο και άρα τα τρίγωνα έχουν λόγο ομοιότητας
και άρα τα τρίγωνα έχουν λόγο ομοιότητας  . Επομένως,
. Επομένως,  .
. θα είναι
θα είναι  . Άρα,
. Άρα,  .
. . Ακόμα με Π.Θ προκύπτει
. Ακόμα με Π.Θ προκύπτει  .
.  .
.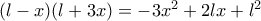
 για
για  .
. για
για  .
.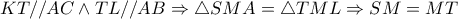


 γίνεται μέγιστο για
γίνεται μέγιστο για 

KARKAR έγραψε:Στην πλευρά- μήκους
- ισοπλεύρου τριγώνου
, κινείται σημείο

Στην προέκταση της βάσηςπαίρνω σημείο
, ώστε

α) Δείξτε ότι το μέσοτου τμήματος
, κινείται επί της

β) Ανοι προβολές των
στην
, υπολογίστε το μέγιστο εμβαδόν του
 παραλ/μμο
παραλ/μμο


 μέσον της
μέσον της  άρα
άρα 
 όταν
όταν  που ισχύει για
που ισχύει για  και
και 
Kαλησπέρα και η λύση μου θυμίζει ....Ανώγεια ...όσοι παρακολούθησαν την Διημερίδα Γεωμετρίας θα καταλάβουν..KARKAR έγραψε:Στην πλευρά- μήκους
- ισοπλεύρου τριγώνου
, κινείται σημείο

Στην προέκταση της βάσηςπαίρνω σημείο
, ώστε

α) Δείξτε ότι το μέσοτου τμήματος
, κινείται επί της

β) Ανοι προβολές των
στην
, υπολογίστε το μέγιστο εμβαδόν του
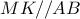 ,άρα το τρίγωνο
,άρα το τρίγωνο  είναι ισόπλευρο .Θέτουμε
είναι ισόπλευρο .Θέτουμε  .Στο τρίγωνο
.Στο τρίγωνο  εφαρμόζουμε το Θεώρημα του Μενελάου με τέμνουσα την
εφαρμόζουμε το Θεώρημα του Μενελάου με τέμνουσα την  , κόκκινη γραμμή,
, κόκκινη γραμμή, 

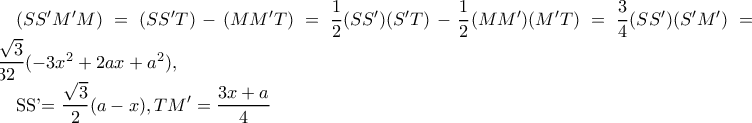

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες