Καλημέρα Θανάση και Ευθύμη,
ξεκινώ ανάποδα και έστω

το ύψος από το

στην

που χωριζει το τμήμα

σε

(από αριστερά προς τα δεξιά)
προφανώς ισχύει

.....(1) και απ'τα όμοια ορθ. τρίγωνα

απόπου

δηλ.

και σε συνδυασμό με την (1) προκύπτει

ή αλλοιώς

.....(2)
α. Οταν το

είναι μέσον του ημικυκλίου, αφενός

και αφετέρου

απόπου

β. Είναι φανερό

.
Αν

τότε και

απόπου

άτοπο λόγω της (2)
Αν

τότε


άτοπο
Αρα

γ. Είναι φανερό από τη (2) ότι για να είναι τα

όροι Α.Π. πρέπει να ισχύει η ισότητα, που συμβαίνει όταν το

είναι μέσον και

, αλλά τότε

(καταχρηστικά Α.Π. με διαφορά

)
Φιλικά Σάκης
''Οσοι σου λένε δεν μπορείς, είναι πιθανότατα αυτοί, που φοβούνται μήπως τα καταφέρεις''
Νίκος Καζαντζάκης
 και με διάμετρο την
και με διάμετρο την  , γράφουμε ημικύκλιο και έστω
, γράφουμε ημικύκλιο και έστω 
 τέμνουν την
τέμνουν την  σε δύο σημεία , σχηματίζοντας τα τμήματα
σε δύο σημεία , σχηματίζοντας τα τμήματα  .
. είναι το μέσο του τόξου δείξτε ότι
είναι το μέσο του τόξου δείξτε ότι 
 βρίσκεται πλησιέστερα προς το
βρίσκεται πλησιέστερα προς το  , δείξτε ότι
, δείξτε ότι  .
.  να είναι διαδοχικοί όροι αριθμητικής προόδου ?
να είναι διαδοχικοί όροι αριθμητικής προόδου ?
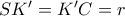 και
και 

 Όμοια και
Όμοια και 
 . Όμοια και
. Όμοια και  . Άρα και
. Άρα και 
 και
και  Επίσης είναι
Επίσης είναι 

 Όμοια και
Όμοια και  και
και 
 εύκολα συμπεραίνουμε ότι
εύκολα συμπεραίνουμε ότι 



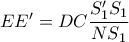


 , άρα τα τμήματα
, άρα τα τμήματα  δεν μπορεί να είναι όροι αριθμητικής προόδου.
δεν μπορεί να είναι όροι αριθμητικής προόδου. το ύψος από το
το ύψος από το  που χωριζει το τμήμα
που χωριζει το τμήμα  σε
σε  (από αριστερά προς τα δεξιά)
(από αριστερά προς τα δεξιά) .....(1) και απ'τα όμοια ορθ. τρίγωνα
.....(1) και απ'τα όμοια ορθ. τρίγωνα  απόπου
απόπου  δηλ.
δηλ.  και σε συνδυασμό με την (1) προκύπτει
και σε συνδυασμό με την (1) προκύπτει  ή αλλοιώς
ή αλλοιώς  .....(2)
.....(2) και αφετέρου
και αφετέρου  απόπου
απόπου 
 .
.  τότε και
τότε και  απόπου
απόπου  άτοπο λόγω της (2)
άτοπο λόγω της (2) τότε
τότε 
 άτοπο
άτοπο
 όροι Α.Π. πρέπει να ισχύει η ισότητα, που συμβαίνει όταν το
όροι Α.Π. πρέπει να ισχύει η ισότητα, που συμβαίνει όταν το  )
) και
και 
 είναι ρίζες της εξίσωσης
είναι ρίζες της εξίσωσης 
 και γεωμετρικής προόδου
και γεωμετρικής προόδου 

 , άτοπο.
, άτοπο. η πλευρά του τετραγώνου
η πλευρά του τετραγώνου  τετράγωνο με
τετράγωνο με  και
και  και ομοίως
και ομοίως  άρα και
άρα και 
 πλησιέστερο του
πλησιέστερο του  και
και  η νέα θέση του
η νέα θέση του  .Ισχύει
.Ισχύει  κι ας υποθέσουμε ότι
κι ας υποθέσουμε ότι  οπότε
οπότε άτοπο
άτοπο κι επομένως
κι επομένως 
 αποτελούν δ.όρους α. προόδου θα ισχύει
αποτελούν δ.όρους α. προόδου θα ισχύει  και
και 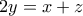 άρα
άρα 
 (βλέπε πρώτη περίπτωση)
(βλέπε πρώτη περίπτωση)  άτοπο
άτοπο