 εφάπτεται των πλευρών
εφάπτεται των πλευρών  στα
στα  .
.Η διχοτόμος της
 τέμνει το τμήμα
τέμνει το τμήμα  στο σημείο
στο σημείο  . Δείξτε ότι
. Δείξτε ότι 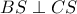 .
.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 εφάπτεται των πλευρών
εφάπτεται των πλευρών  στα
στα  .
. τέμνει το τμήμα
τέμνει το τμήμα  στο σημείο
στο σημείο  . Δείξτε ότι
. Δείξτε ότι 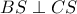 .
. το σημείο που εφάπτεται ο έγκυκλος στην
το σημείο που εφάπτεται ο έγκυκλος στην  . Φέρνουμε τα τμήματα
. Φέρνουμε τα τμήματα  και
και  .
.  , άρα το τρίγωνο
, άρα το τρίγωνο 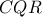 είναι ισοσκελές, συνεπώς η διχοτόμος
είναι ισοσκελές, συνεπώς η διχοτόμος  είναι και μεσοκάθετος στο
είναι και μεσοκάθετος στο  , άρα
, άρα  .
. 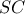 είναι διχοτόμος της
είναι διχοτόμος της  , το
, το  είναι χαρταετός και
είναι χαρταετός και  (1).
(1). είναι διχοτόμος της
είναι διχοτόμος της 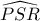 .
. είναι ισοσκελές, άρα
είναι ισοσκελές, άρα  (2).
(2).  . Άρα το
. Άρα το  είναι εγγεγραμμένο.
είναι εγγεγραμμένο.  , προκύπτει ότι το σημείο
, προκύπτει ότι το σημείο  αποτελεί την τομή του περιγεγραμμένου κύκλου του τριγώνου
αποτελεί την τομή του περιγεγραμμένου κύκλου του τριγώνου  με την μεσοκάθετη του
με την μεσοκάθετη του  . Άρα από το αντίστροφο του θεωρήματος του νότιου πόλου προκύπτει ότι η
. Άρα από το αντίστροφο του θεωρήματος του νότιου πόλου προκύπτει ότι η  είναι διχοτόμος της
είναι διχοτόμος της 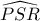 και το ζητούμενο έπεται.
και το ζητούμενο έπεται.KARKAR έγραψε:Αξιόλογη καθετότητα.pngΟ έγκυκλος του τριγώνουεφάπτεται των πλευρών
στα
.
Η διχοτόμος τηςτέμνει το τμήμα
στο σημείο
. Δείξτε ότι
.
 το σημείο επαφής του
το σημείο επαφής του 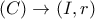 με την
με την  και
και  η τομή των ευθειών
η τομή των ευθειών  ( πολική του
( πολική του  ως προς
ως προς  ).
). είναι αρμονικά συζυγή των
είναι αρμονικά συζυγή των  .
. με τέμνουσα την ευθεία
με τέμνουσα την ευθεία  και το Θ. Μενελάου έχουμε:
και το Θ. Μενελάου έχουμε: γιατί τα εφαπτόμενα τμήματα σε κύκλο είναι ίσα.
γιατί τα εφαπτόμενα τμήματα σε κύκλο είναι ίσα.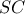 διχοτομεί την
διχοτομεί την  θα είναι και η
θα είναι και η  εσωτερική διχοτόμος του
εσωτερική διχοτόμος του  και άρα
και άρα  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες