 τέτοιες, ώστε
τέτοιες, ώστε 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 (1)
(1)

 (2)
(2)

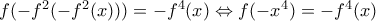 (3)
(3)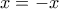

 (4)
(4)


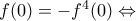
 ή
ή 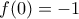
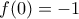 , τότε η (2) για
, τότε η (2) για  δίνει
δίνει  και η (4) για
και η (4) για 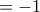 δίνει
δίνει 






 η οποία για
η οποία για  δίνει
δίνει  . Όμως η (2) για
. Όμως η (2) για  δίνει
δίνει  που είναι άτοπο.
που είναι άτοπο. .
. με
με 
 , λόγω της (2) ,
, λόγω της (2) , 
 λοιπόν είναι
λοιπόν είναι  στο
στο  .
.

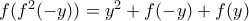 , η οποία για
, η οποία για  γίνεται :
γίνεται :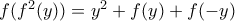 . Από τις δύο τελευταίες προκύπτει ότι :
. Από τις δύο τελευταίες προκύπτει ότι :  και καθώς τα
και καθώς τα  και
και  είναι ποσότητες μη αρνητικές, θα είναι
είναι ποσότητες μη αρνητικές, θα είναι  (5)
(5) και
και 







 ,
,


 για
για 

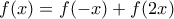

 για
για 



 ,
,
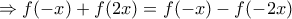 , που για
, που για  δίνει
δίνει 

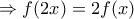
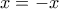 και
και 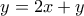


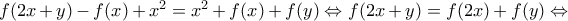
 .
. σαφώς "επί" συνάρτηση, επομένως
σαφώς "επί" συνάρτηση, επομένως 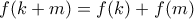 για κάθε
για κάθε 

 και
και 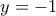



 . Άρα
. Άρα  ή
ή  .
. δίνει :
δίνει : 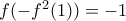 . Αν
. Αν  καταλήγουμε σε άτοπο. Επομένως
καταλήγουμε σε άτοπο. Επομένως  και
και  .
. και
και 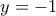




 . Η
. Η  "1-1" και "επί".
"1-1" και "επί".



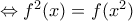 , η οποία για
, η οποία για  δίνει :
δίνει :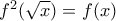 , που σημαίνει ότι για κάθε
, που σημαίνει ότι για κάθε  η
η  είναι μη αρνητική. Άρα είναι Cauchy, άρα
είναι μη αρνητική. Άρα είναι Cauchy, άρα 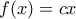 .
. θα είναι
θα είναι 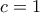 . Άρα
. Άρα  , που επαληθεύει την (1).
, που επαληθεύει την (1). μπορούμε να προχωρήσουμε παρατηρώντας ότι, από την (3) και την περιττή συμμετρία,
μπορούμε να προχωρήσουμε παρατηρώντας ότι, από την (3) και την περιττή συμμετρία, 
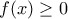 όταν
όταν 
υπάρχει εδώ:Να προσδιορίσετε όλες τις συναρτήσειςτέτοιες, ώστε
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες