Αν
 είναι δύο θετικοί άρρητοι αριθμοί με
είναι δύο θετικοί άρρητοι αριθμοί με  και
και ![A=\left\{[na]/n\in N \right\}, B=\left\{[nb]/n\in N \right\} A=\left\{[na]/n\in N \right\}, B=\left\{[nb]/n\in N \right\}](/forum/ext/geomar/texintegr/latexrender/pictures/6753f885a62c4802128ed26863d28ce5.png) Να αποδείξετε ότι
Να αποδείξετε ότι  και
και  . Όπου
. Όπου  το σύνολο των φυσικών αριθμών και
το σύνολο των φυσικών αριθμών και ![[na] [na]](/forum/ext/geomar/texintegr/latexrender/pictures/e30daa640cf8f17a238283b55c100bbc.png) σημαίνει το ακέραιο μέρος του
σημαίνει το ακέραιο μέρος του 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 είναι δύο θετικοί άρρητοι αριθμοί με
είναι δύο θετικοί άρρητοι αριθμοί με  και
και ![A=\left\{[na]/n\in N \right\}, B=\left\{[nb]/n\in N \right\} A=\left\{[na]/n\in N \right\}, B=\left\{[nb]/n\in N \right\}](/forum/ext/geomar/texintegr/latexrender/pictures/6753f885a62c4802128ed26863d28ce5.png) Να αποδείξετε ότι
Να αποδείξετε ότι  και
και  . Όπου
. Όπου  το σύνολο των φυσικών αριθμών και
το σύνολο των φυσικών αριθμών και ![[na] [na]](/forum/ext/geomar/texintegr/latexrender/pictures/e30daa640cf8f17a238283b55c100bbc.png) σημαίνει το ακέραιο μέρος του
σημαίνει το ακέραιο μέρος του 
 υπάρχουν
υπάρχουν  πολλπλάσια του
πολλπλάσια του  μικρότερα από
μικρότερα από  και
και  πολλαπλάσια του
πολλαπλάσια του  μικρότερα από
μικρότερα από  . Αυτό γιατί οι αριθμοί της μορφής
. Αυτό γιατί οι αριθμοί της μορφής  και
και  δεν είναι ποτέ ακέραιοι. Από την
δεν είναι ποτέ ακέραιοι. Από την  είναι
είναι 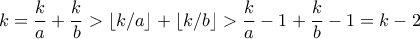 άρα
άρα  . Πάει να πει, ακριβώς
. Πάει να πει, ακριβώς  αριθμοί της μορφής
αριθμοί της μορφής  ή
ή  είναι μικρότεροι από
είναι μικρότεροι από  . Όμοια, ακριβώς
. Όμοια, ακριβώς  αριθμοί της μορφής
αριθμοί της μορφής  ή
ή  είναι μικρότεροι από
είναι μικρότεροι από  . Έτσι, μέσα στο
. Έτσι, μέσα στο  υπάρχει ακριβώς ένας
υπάρχει ακριβώς ένας  ή ακριβώς ένας
ή ακριβώς ένας  .
. , αρκεί να αποδείξουμε ότι δεν υπάρχουν φυσικοί
, αρκεί να αποδείξουμε ότι δεν υπάρχουν φυσικοί  τέτοιοι ώστε
τέτοιοι ώστε  και
και  . Έστω πως ισχύει το αντίθετο, τότε
. Έστω πως ισχύει το αντίθετο, τότε 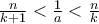 και
και  , άρα
, άρα  , δηλαδή
, δηλαδή  , άτοπο.
, άτοπο. , αρκεί να δειχθεί ότι δεν υπάρχει φυσικός αριθμός
, αρκεί να δειχθεί ότι δεν υπάρχει φυσικός αριθμός  , ώστε στο διάστημα
, ώστε στο διάστημα  να μη περιέχεται πολλαπλάσιο της μορφής
να μη περιέχεται πολλαπλάσιο της μορφής  και της μορφής
και της μορφής  , όπου
, όπου  φυσικοί αριθμοί.
φυσικοί αριθμοί. και
και 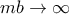 , καθώς
, καθώς  , θα υπάρχουν
, θα υπάρχουν  , ώστε
, ώστε 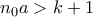 ,
,  και
και  . Συνεπώς
. Συνεπώς  και
και  , δηλαδή
, δηλαδή  , άτοπο.
, άτοπο. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες