Έχουμε

δυάδες
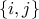
με
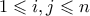
και

. Την δυάδα
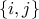
θα την χρησιμοποιήσω δύο φορές, από μία για κάθε ένα σημείο τομής των κύκλων

και

.
Το παιχνίδι λέει ότι κάθε παίκτης επιλέγει μια δυάδα που έχει επιλεχθεί το πολύ μία φορά αρκεί κανένα από τα στοιχεία της δυάδας του να μην ισούται με κάποιο από τα στοιχεία της δυάδας που επέλεξε ο άλλος παίκτης στην αμέσως προηγούμενη κίνηση. Αν κάποιος παίκτης δεν μπορεί να κινηθεί χάνει.
Για

είναι προφανές πως κερδίζει ο πρώτος

αφού επιλέγει την

και ο

δεν μπορεί να κάνει τίποτα.
Θα δείξω ότι για κάθε

κερδίζει ο

.
Αρχικά ο

χωρίζει τις πιο πάνω δυάδες σε ζεύγη ως εξής:
(α) Την δυάδα
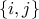
με
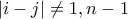
την βάζει μια φορά με την δυάδα
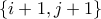
και μια με την
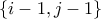
. Εδώ όλες οι πράξεις είναι

.
(β) Την δυάδα

την βάζει μια φορά με την

και μια με την
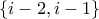
. [Επιτρέπεται διότι

.]
Τώρα έχουμε

ζεύγη δυάδων. Κάθε φορά που ο

επιλέγει μία δυάδα, ο

επιλέγει μια άλλη που βρίσκεται στο ίδιο ζεύγος με την δυάδα του

και διαγράφει αυτό το ζεύγος. Οπότε όταν το παιγνίδι τελειώσει πρέπει να είναι η σειρά του

να κινηθεί και ο

δεν χάνει όπως θέλαμε να δείξουμε.

Αν γνωρίζουμε το
θεώρημα του γάμου., δεν χρειάζεται καν να κάνουμε την κατασκευή. Βάζουμε στην ομάδα

τα ζεύγη
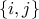
από μία φορά το κάθε ένα και στην ομάδα

τα ίδια ζεύγη από μία φορά το κάθε ένα. Συνδέουμε ένα ζεύγος του

με ένα ζεύγος του

αν και μόνο αν τα δύο ζεύγη δεν έχουν κοινό στοιχείο.
Αρκεί να βρούμε ένα πλήρες ταίριασμα για να χρησιμοποιήσουμε την προηγούμενη στρατηγική. Κάθε κορυφή είτε του

είτε του

έχει βαθμό ακριβώς

. Είναι όμως απλή συνέπεια του θεωρήματος του γάμου ότι κάθε διμερές γράφημα όπου όλες οι κορυφές έχουν τον ίδιο βαθμό έχει ένα πλήρες ταίριασμα.
Το αφήνω ως άσκηση.
 κύκλους στο επίπεδο έτσι ώστε ανά δύο να τέμνονται και ανά τρεις να μην διέρχονται από το ίδιο σημείο. Αρχικά υπάρχει ένα κέρμα σε κάθε σημείο τομής που ορίζουν οι κύκλοι. Δύο παίκτες
κύκλους στο επίπεδο έτσι ώστε ανά δύο να τέμνονται και ανά τρεις να μην διέρχονται από το ίδιο σημείο. Αρχικά υπάρχει ένα κέρμα σε κάθε σημείο τομής που ορίζουν οι κύκλοι. Δύο παίκτες  παίζουν το εξής παιχνίδι. Ξεκινάει ο
παίζουν το εξής παιχνίδι. Ξεκινάει ο  και οι παίκτες παίζουν εναλλάξ αφαιρώντας ένα κέρμα την φορά. Η μόνη προϋπόθεση είναι ότι όταν ένας παίκτης αφαιρεί ένα κέρμα από το σημείο τομής δύο κύκλων , τότε ο άλλος παίκτης στην αμέσως επόμενη κίνηση απαγορεύεται να αφαιρέσει κέρμα από σημείο που ανήκει σε έναν από τους δύο κύκλους (ή και στους δύο ). Ένας παίκτης χάνει όταν δεν μπορεί να πραγματοποιήσει επιπλέον κίνηση. Να βρείτε τα
και οι παίκτες παίζουν εναλλάξ αφαιρώντας ένα κέρμα την φορά. Η μόνη προϋπόθεση είναι ότι όταν ένας παίκτης αφαιρεί ένα κέρμα από το σημείο τομής δύο κύκλων , τότε ο άλλος παίκτης στην αμέσως επόμενη κίνηση απαγορεύεται να αφαιρέσει κέρμα από σημείο που ανήκει σε έναν από τους δύο κύκλους (ή και στους δύο ). Ένας παίκτης χάνει όταν δεν μπορεί να πραγματοποιήσει επιπλέον κίνηση. Να βρείτε τα  για τα οποία ο
για τα οποία ο  έχει στρατηγική νίκης.
έχει στρατηγική νίκης.
 δυάδες
δυάδες 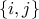 με
με 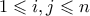 και
και  . Την δυάδα
. Την δυάδα  και
και  .
. είναι προφανές πως κερδίζει ο πρώτος
είναι προφανές πως κερδίζει ο πρώτος  και ο
και ο  κερδίζει ο
κερδίζει ο 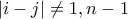 την βάζει μια φορά με την δυάδα
την βάζει μια φορά με την δυάδα 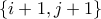 και μια με την
και μια με την 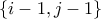 . Εδώ όλες οι πράξεις είναι
. Εδώ όλες οι πράξεις είναι  .
. την βάζει μια φορά με την
την βάζει μια φορά με την  και μια με την
και μια με την 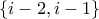 . [Επιτρέπεται διότι
. [Επιτρέπεται διότι 
 τα ζεύγη
τα ζεύγη  τα ίδια ζεύγη από μία φορά το κάθε ένα. Συνδέουμε ένα ζεύγος του
τα ίδια ζεύγη από μία φορά το κάθε ένα. Συνδέουμε ένα ζεύγος του  . Είναι όμως απλή συνέπεια του θεωρήματος του γάμου ότι κάθε διμερές γράφημα όπου όλες οι κορυφές έχουν τον ίδιο βαθμό έχει ένα πλήρες ταίριασμα. Το αφήνω ως άσκηση.
. Είναι όμως απλή συνέπεια του θεωρήματος του γάμου ότι κάθε διμερές γράφημα όπου όλες οι κορυφές έχουν τον ίδιο βαθμό έχει ένα πλήρες ταίριασμα. Το αφήνω ως άσκηση.