Μεσογειάδα 2008 (γεωμετρία)
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
Μεσογειάδα 2008 (γεωμετρία)
Έστω c ο παρεγεγγραμμένος κύκλος τριγώνου ΑΒC με κέντρο το Ι, ο οποίος εφάπτεται της BC στο D και των προεκτάσεων των AC, AB στα Ε,Ζ αντιστοίχως. Η ED είναι κάθετη στην ΑΒ και την τεμνει στο Η. Η ZF είναι η κάθετη από το Ζ προς την ΗΙ την οποία τέμνει στο F. Να υπολογίσετε τις γωνίες BFD , AFE
Στο συνημμένο έχω την λύση όχι με τον κλασικό τρόπο (Ευκλείδεια) αλλά και με τριγωνομετρία.
Ακόμη χρειάστηκα το "αντίστροφο" του Απολλώνειου κύκλου δηλαδή
Στην προεκταση της διαμέτρου BC κύκλου (c) βρίσκεται σημείο Χ Αν τα C,B,X,Y είναι συζυγή αρμονικά και Α τυχαίο σημείο του κύκλου τότε η BΑ είναι διχοτόμος της ΥΑΧ που και εκει κάνω την απόδειξη με μιγαδικούς και όχι με τον παραδεδεγμένο τρόπο (Ευκλείδεια)
Στο συνημμένο έχω την λύση όχι με τον κλασικό τρόπο (Ευκλείδεια) αλλά και με τριγωνομετρία.
Ακόμη χρειάστηκα το "αντίστροφο" του Απολλώνειου κύκλου δηλαδή
Στην προεκταση της διαμέτρου BC κύκλου (c) βρίσκεται σημείο Χ Αν τα C,B,X,Y είναι συζυγή αρμονικά και Α τυχαίο σημείο του κύκλου τότε η BΑ είναι διχοτόμος της ΥΑΧ που και εκει κάνω την απόδειξη με μιγαδικούς και όχι με τον παραδεδεγμένο τρόπο (Ευκλείδεια)
- Συνημμένα
-
- forum 58.doc
- (68.5 KiB) Μεταφορτώθηκε 99 φορές
- vittasko
- Επιμελητής
- Δημοσιεύσεις: 2230
- Εγγραφή: Πέμ Ιαν 08, 2009 8:46 am
- Τοποθεσία: Μαρούσι - Αθήνα.
- Επικοινωνία:
Re: Μεσογειάδα 2008 (γεωμετρία)
Η ευθεία  είναι η πολική του σημείου
είναι η πολική του σημείου  ως προς τον κύκλο
ως προς τον κύκλο  τον παρεγγεγραμμένο κύκλο του
τον παρεγγεγραμμένο κύκλο του  στη γωνία
στη γωνία  (αντί του (Ι) στην εκφώνηση ).
(αντί του (Ι) στην εκφώνηση ).
Επειδή η περνάει από το σημείο
περνάει από το σημείο  έχουμε ότι η πολική του
έχουμε ότι η πολική του  ως προς τον ίδιο κύκλο, περνάει από το σημείο
ως προς τον ίδιο κύκλο, περνάει από το σημείο 
Η ευθεία τώρα είναι η πολική του
είναι η πολική του  ως προς τον
ως προς τον  γιατί είναι κάθετη επί την ευθεία
γιατί είναι κάθετη επί την ευθεία  και περνάει από
και περνάει από  ( το σημείο επαφής της εφαπτομένης του
( το σημείο επαφής της εφαπτομένης του  από το
από το  ).
).
Συμπεραίνουμε επομένως, ότι τα σημεία είναι συνευθειακά και έστω το σημείο
είναι συνευθειακά και έστω το σημείο 
 Είναι γνωστό ότι τα σημεία
Είναι γνωστό ότι τα σημεία  είναι αρμονικά συζυγή, ως σημεία τομής της ευθείας δια του
είναι αρμονικά συζυγή, ως σημεία τομής της ευθείας δια του  από τον κύκλο
από τον κύκλο  και την πολική του
και την πολική του  ως προς αυτόν.
ως προς αυτόν.
Άρα η δέσμη είναι αρμονική και επειδή
είναι αρμονική και επειδή  συμπεραίνουμε ότι η ευθεία
συμπεραίνουμε ότι η ευθεία  διχοτομεί τη γωνία
διχοτομεί τη γωνία  και άρα έχουμε
και άρα έχουμε 

Η δέσμη είναι επίσης αρμονική και τεμνόμενη από την ευθεία
είναι επίσης αρμονική και τεμνόμενη από την ευθεία  μας δίνει την αρμονική σημειοσειρά
μας δίνει την αρμονική σημειοσειρά 
Έτσι, η δέσμη είναι αρμονική και επειδή έχουμε
είναι αρμονική και επειδή έχουμε  συμπεραίνουμε ότι η ευθεία
συμπεραίνουμε ότι η ευθεία  διχοτομεί τη γωνία
διχοτομεί τη γωνία  και άρα έχουμε
και άρα έχουμε 

 Από εγγράψιμο τετράπλευρο
Από εγγράψιμο τετράπλευρο  έχουμε ότι
έχουμε ότι 
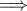

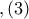
Από προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο και ακολουθεί το συμπέρασμα ότι
είναι εγγράψιμο και ακολουθεί το συμπέρασμα ότι 

Από εγγράψιμο έχουμε επίσης
έχουμε επίσης 

Από
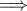


Από προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.
Συμπεραίνουμε έτσι, ότι
 και το πρόβλημα έχει λυθεί.
και το πρόβλημα έχει λυθεί.
Κώστας Βήττας.
 είναι η πολική του σημείου
είναι η πολική του σημείου  ως προς τον κύκλο
ως προς τον κύκλο  τον παρεγγεγραμμένο κύκλο του
τον παρεγγεγραμμένο κύκλο του  στη γωνία
στη γωνία  (αντί του (Ι) στην εκφώνηση ).
(αντί του (Ι) στην εκφώνηση ).Επειδή η
 περνάει από το σημείο
περνάει από το σημείο  έχουμε ότι η πολική του
έχουμε ότι η πολική του  ως προς τον ίδιο κύκλο, περνάει από το σημείο
ως προς τον ίδιο κύκλο, περνάει από το σημείο 
Η ευθεία τώρα
 είναι η πολική του
είναι η πολική του  ως προς τον
ως προς τον  γιατί είναι κάθετη επί την ευθεία
γιατί είναι κάθετη επί την ευθεία  και περνάει από
και περνάει από  ( το σημείο επαφής της εφαπτομένης του
( το σημείο επαφής της εφαπτομένης του  από το
από το  ).
). Συμπεραίνουμε επομένως, ότι τα σημεία
 είναι συνευθειακά και έστω το σημείο
είναι συνευθειακά και έστω το σημείο 
 Είναι γνωστό ότι τα σημεία
Είναι γνωστό ότι τα σημεία  είναι αρμονικά συζυγή, ως σημεία τομής της ευθείας δια του
είναι αρμονικά συζυγή, ως σημεία τομής της ευθείας δια του  από τον κύκλο
από τον κύκλο  και την πολική του
και την πολική του  ως προς αυτόν.
ως προς αυτόν.Άρα η δέσμη
 είναι αρμονική και επειδή
είναι αρμονική και επειδή  συμπεραίνουμε ότι η ευθεία
συμπεραίνουμε ότι η ευθεία  διχοτομεί τη γωνία
διχοτομεί τη γωνία  και άρα έχουμε
και άρα έχουμε 

Η δέσμη
 είναι επίσης αρμονική και τεμνόμενη από την ευθεία
είναι επίσης αρμονική και τεμνόμενη από την ευθεία  μας δίνει την αρμονική σημειοσειρά
μας δίνει την αρμονική σημειοσειρά 
Έτσι, η δέσμη
 είναι αρμονική και επειδή έχουμε
είναι αρμονική και επειδή έχουμε  συμπεραίνουμε ότι η ευθεία
συμπεραίνουμε ότι η ευθεία  διχοτομεί τη γωνία
διχοτομεί τη γωνία  και άρα έχουμε
και άρα έχουμε 

 Από εγγράψιμο τετράπλευρο
Από εγγράψιμο τετράπλευρο  έχουμε ότι
έχουμε ότι 
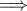

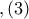
Από
 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο και ακολουθεί το συμπέρασμα ότι
είναι εγγράψιμο και ακολουθεί το συμπέρασμα ότι 

Από εγγράψιμο
 έχουμε επίσης
έχουμε επίσης 

Από



Από
 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.Συμπεραίνουμε έτσι, ότι

 και το πρόβλημα έχει λυθεί.
και το πρόβλημα έχει λυθεί.Κώστας Βήττας.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
