Έστω κυρτό τετράπλευρο
 με διαγώνιους τις
με διαγώνιους τις  .
.Αν οι γωνίες
 έχουν αντίστοιχα μέτρο
έχουν αντίστοιχα μέτρο  και επίσης είναι
και επίσης είναι  .
.Βρείτε τον αριθμό των μοιρών που εκφράζει το
 .
.Live Practice >>>>>>>
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
 με διαγώνιους τις
με διαγώνιους τις  .
. έχουν αντίστοιχα μέτρο
έχουν αντίστοιχα μέτρο  και επίσης είναι
και επίσης είναι  .
. .
.
Καλησπέρα!Δημήτρης Μυρογιάννης έγραψε:Την έχουμε ξαναδεί με μοναδική λύση νομίζω.
Έστω κυρτό τετράπλευρομε διαγώνιους τις
.
Αν οι γωνίεςέχουν αντίστοιχα μέτρο
και επίσης είναι
.
Βρείτε τον αριθμό των μοιρών που εκφράζει το.
Live Practice >>>>>>>
 (1),
(1), (2).
(2). είναι ισοσκελή, άρα
είναι ισοσκελή, άρα  .
. .
. , και λόγω μονοτονίας,
, και λόγω μονοτονίας, 
Καλησπέρα!Δημήτρης Μυρογιάννης έγραψε:Την έχουμε ξαναδεί με μοναδική λύση νομίζω.
Έστω κυρτό τετράπλευρομε διαγώνιους τις
.
Αν οι γωνίεςέχουν αντίστοιχα μέτρο
και επίσης είναι
.
Βρείτε τον αριθμό των μοιρών που εκφράζει το.
geometrein-104.PNG
Live Practice >>>>>>>
 . Είναι
. Είναι  και
και  Είναι ακόμα:
Είναι ακόμα:





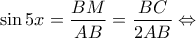


 κατά μέλη:
κατά μέλη: 


 ,
, , η
, η  διχοτόμος της
διχοτόμος της  ,
,
 με
με  έχουμε
έχουμε  ,άρα η
,άρα η  είναι διχοτόμος και
είναι διχοτόμος και 

Πολύ καλό ΦωτεινήΦωτεινή έγραψε:Καλησπέρα Δημήτρη ,Ορέστη και Γιώργο.
-----------------------------------------------------
Σχηματίζουμε το ισόπλευρο,
, η
διχοτόμος της
,
Στο ισοσκελέςμε
έχουμε
,άρα η
είναι διχοτόμος και
104-.png
 και έστω
και έστω  το κέντρο του.
το κέντρο του.  που φυσικά είναι
που φυσικά είναι  . Παρατηρούμε τη σχέση της εγγεγραμμένης
. Παρατηρούμε τη σχέση της εγγεγραμμένης 
 που κατοχυρώνει το ισόπλευρο τρίγωνο
που κατοχυρώνει το ισόπλευρο τρίγωνο  .
. ):
):  .
. τα ίσα τρίγωνα
τα ίσα τρίγωνα  , κάτι που (και εδώ πολύ εύκολα)
, κάτι που (και εδώ πολύ εύκολα)  με μέτρο
με μέτρο  και ουσιαστικά ολοκληρώνει τη λύση.
και ουσιαστικά ολοκληρώνει τη λύση.
Δημήτρη καλημέρα.Δημήτρης Μυρογιάννης έγραψε:Φωτεινή, Γιώργο και Ορέστη (Ορέστη τι ακριβώς είσαι δεν έχω καταλάβει) ευχαριστώ.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης