Άσπρες και μαύρες μπάλες
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Άσπρες και μαύρες μπάλες
Σε ένα καλάθι έχουμε 100 άσπρες και 99 μαύρες μπάλες. Παίρνουμε ομοιόμορφα στην τύχη μια μπάλα και την αφαιρούμε. Μετά συνεχίζουμε να παίρνουμε ομοιόμορφα στην τύχη μπάλες και να τις αφαιρούμε μέχρις ότου βρούμε μπάλα διαφορετικού χρώματος από την πρώτη που αφαιρέσαμε. Αυτήν την μπάλα την επανατοποθετούμε στο καλάθι και ξαναρχίζουμε την διαδικασία από την αρχή. (Η επόμενη μπάλα που θα αφαιρεθεί μπορεί να είναι οποιουδήποτε χρώματος.) Να βρεθεί η πιθανότητα η τελευταία μπάλα που θα μείνει στο καλάθι να είναι άσπρη.
Re: Άσπρες και μαύρες μπάλες
100/199, είναι η ίδια πιθανότητα με την πιθανότητα στην 1η θέση να έρθει λευκή μπάλα.
What's wrong with a Greek in Hamburg?
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Άσπρες και μαύρες μπάλες
Όχι δεν είναι η ίδια πιθανότητα. Δες π.χ την περίπτωση 2 άσπρες και 1 μαύρη. Η σωστή απάντηση σε αυτό (θέλει λίγη δουλειά) δεν είναι 2/3.
Re: Άσπρες και μαύρες μπάλες
Ok θα το ξανασκεφτώ, αν πάρω την πιθανότητα να έρθουν όλες οι μαύρες πρώτα είμαι κοντά; Θα το δω με το απλό δείγμα των τριών που ανέφερες Ok.
What's wrong with a Greek in Hamburg?
Re: Άσπρες και μαύρες μπάλες
Δημήτρη δεν καταλαβαίνω ο δειγματοχώρος για τρεις μπάλες είναι {AAM,AMA,ΜΑΑ}, επομένως γιατί να μην είναι 2/3; Δηλαδή από τα 3 ισοπίθανα ενδεχόμενα τα 2 ικανοποιούν την συνθήκη που θέλουμε.
What's wrong with a Greek in Hamburg?
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Άσπρες και μαύρες μπάλες
Δεν είναι ισοπίθανα όμως. Επειδή ίσως να μην έγινε κατανοητή η διαδικασία ευκαιρία να την ξαναεξηγήσω.
Έστω έχουμε 2 άσπρες και 1 μαύρη. Τότε μπορούν να συμβούν τα εξής:
Περίπτωση 1: Η πρώτη μπάλα είναι άσπρη. Την αφαιρούμε και μένουν μία άσπρη και μία μαύρη.
Περίπτωση 1Α: Η δεύτερη μπάλα είναι άσπρη. Την αφαιρούμε και μένει μόνο η μαύρη.
Περίπτωση 1Β: Η δεύτερη μπάλα είναι μαύρη, Σε αυτήν την περίπτωση, επειδή η πρώτη ήταν άσπρη δεν αφαιρούμε την μπάλα αλλά την επανατοποθετούμε και ξαναρχίζουμε την διαδικασία από την αρχή. Τώρα έχουμε μία άσπρη και μία μαύρη και επειδή η διαδικασία έχει ξαναρχίσει, οποιαδήποτε χρώμα πάρουμε το αφαιρούμε.
Ομοίως και οι άλλες περιπτώσεις.
[Αν δεν υπήρχε η συνθήκη της επανατοποθέτησης τότε το είναι όντως σωστό.]
είναι όντως σωστό.]
Έστω έχουμε 2 άσπρες και 1 μαύρη. Τότε μπορούν να συμβούν τα εξής:
Περίπτωση 1: Η πρώτη μπάλα είναι άσπρη. Την αφαιρούμε και μένουν μία άσπρη και μία μαύρη.
Περίπτωση 1Α: Η δεύτερη μπάλα είναι άσπρη. Την αφαιρούμε και μένει μόνο η μαύρη.
Περίπτωση 1Β: Η δεύτερη μπάλα είναι μαύρη, Σε αυτήν την περίπτωση, επειδή η πρώτη ήταν άσπρη δεν αφαιρούμε την μπάλα αλλά την επανατοποθετούμε και ξαναρχίζουμε την διαδικασία από την αρχή. Τώρα έχουμε μία άσπρη και μία μαύρη και επειδή η διαδικασία έχει ξαναρχίσει, οποιαδήποτε χρώμα πάρουμε το αφαιρούμε.
Ομοίως και οι άλλες περιπτώσεις.
[Αν δεν υπήρχε η συνθήκη της επανατοποθέτησης τότε το
 είναι όντως σωστό.]
είναι όντως σωστό.]-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Άσπρες και μαύρες μπάλες
Άλλο ένα πρόβλημα πιθανοτήτων στο οποίο η διαίσθηση πάει περίπατο....
Θα αποδείξω εδώ κάτι ισχυρότερο:
Όποιος και αν είναι ο αρχικός αριθμός (θετικός ακέραιος) άσπρων και μαύρων η πιθανότητα είναι .
.
Έστω η πιθανότητα η διαδικασία να τερματιστεί και η τελευταία μπάλα να είναι άσπρη αν ξεκινήσουμε με
η πιθανότητα η διαδικασία να τερματιστεί και η τελευταία μπάλα να είναι άσπρη αν ξεκινήσουμε με  άσπρες και
άσπρες και  μαύρες μπάλες. Προφανώς, για οποιουσδήποτε θετικούς ακέραιους
μαύρες μπάλες. Προφανώς, για οποιουσδήποτε θετικούς ακέραιους  και
και  είναι
είναι  . Έστω
. Έστω  . Ας υποθέσουμε ότι η πρώτη μπάλα που τραβάμε είναι άσπρη. Τότε η διαδικασία μπορεί να ακολουθήσει μια από τις παρακάτω πορείες:
. Ας υποθέσουμε ότι η πρώτη μπάλα που τραβάμε είναι άσπρη. Τότε η διαδικασία μπορεί να ακολουθήσει μια από τις παρακάτω πορείες:
 Οι αντίστοιχες πιθανότητες είναι:
Οι αντίστοιχες πιθανότητες είναι:
Στην τελευταία περίπτωση έχουμε επιλέξει πρώτα όλες τις άσπρες οπότε η διαδικασία τερματίζεται και με πιθανότητα η τελευταία μπάλα είναι άσπρη.
η τελευταία μπάλα είναι άσπρη.
Αν η πρώτη μπάλα που τραβάμε είναι μαύρη τότε η διαδικασία μπορεί να ακολουθήσει μια από τις παρακάτω πορείες:
 με αντίστοιχες πιθανότητες:
με αντίστοιχες πιθανότητες:
Στην τελευταία περίπτωση έχουμε επιλέξει πρώτα όλες τις μαύρες οπότε η διαδικασία τερματίζεται και με πιθανότητα η τελευταία μπάλα είναι άσπρη.
η τελευταία μπάλα είναι άσπρη.
Πρώτη περίπτωση (πρώτη μπάλα άσπρη): Έστω ότι έχουμε επιλέξει συνεχόμενα (μετά την πρώτη μπάλα και μέχρι την αλλαγή χρώματος) άσπρες μπάλες
άσπρες μπάλες  . Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι
. Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι 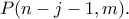
Δεύτερη περίπτωση (πρώτη μπάλα μαύρη): Έστω ότι έχουμε επιλέξει συνεχόμενα (μετά την πρώτη μπάλα και μέχρι την αλλαγή χρώματος) μαύρες μπάλες
μαύρες μπάλες 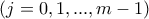 . Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι
. Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι 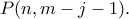
Με βάση την παραπάνω ανάλυση παίρνουμε τελικά την παρακάτω αναγωγική εξίσωση:
![\displaystyle{ P(n,m)=\sum_{j=0}^{n-1}\left [ \prod_{k=0}^{j} \frac{n-k}{n+m-k}\right ] \frac{m}{n+m-j-1} P(n-j-1,m) } \displaystyle{ P(n,m)=\sum_{j=0}^{n-1}\left [ \prod_{k=0}^{j} \frac{n-k}{n+m-k}\right ] \frac{m}{n+m-j-1} P(n-j-1,m) }](/forum/ext/geomar/texintegr/latexrender/pictures/f56aa04d6966bda9301855ff062c8710.png)
![\displaystyle{ +\sum_{j=0}^{m-1}\left [ \prod_{k=0}^{j} \frac{m-k}{n+m-k} \right] \frac{n}{n+m-j-1} \left P(n,m-j-1) } \displaystyle{ +\sum_{j=0}^{m-1}\left [ \prod_{k=0}^{j} \frac{m-k}{n+m-k} \right] \frac{n}{n+m-j-1} \left P(n,m-j-1) }](/forum/ext/geomar/texintegr/latexrender/pictures/faa019a8d9e2a9125045d3fffcd1eee6.png) ή (λίγο) πιο κομψά:
ή (λίγο) πιο κομψά:
 όπου
όπου  και
και 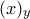 το καθοδικό παραγοντικό
το καθοδικό παραγοντικό  τάξης του
τάξης του  .
.
Προχωράμε τώρα με επαγωγή (ισχυρή) για να δείξουμε ότι για οποιουσδήποτε θετικούς ακέραιους
για οποιουσδήποτε θετικούς ακέραιους  και
και  . Εύκολα ελέγχουμε ότι
. Εύκολα ελέγχουμε ότι  Θα δείξουμε τώρα ότι:
Θα δείξουμε τώρα ότι:
 Είναι
Είναι
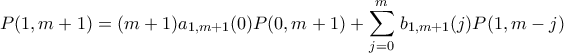
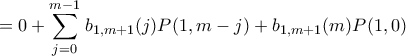

 Όμοια δείχνουμε ότι
Όμοια δείχνουμε ότι  για κάθε
για κάθε  Τελικά, για οποιουσδήποτε θετικούς ακέραιους
Τελικά, για οποιουσδήποτε θετικούς ακέραιους  και
και  είναι
είναι 
Θα αποδείξω εδώ κάτι ισχυρότερο:
Όποιος και αν είναι ο αρχικός αριθμός (θετικός ακέραιος) άσπρων και μαύρων η πιθανότητα είναι
 .
.Έστω
 η πιθανότητα η διαδικασία να τερματιστεί και η τελευταία μπάλα να είναι άσπρη αν ξεκινήσουμε με
η πιθανότητα η διαδικασία να τερματιστεί και η τελευταία μπάλα να είναι άσπρη αν ξεκινήσουμε με  άσπρες και
άσπρες και  μαύρες μπάλες. Προφανώς, για οποιουσδήποτε θετικούς ακέραιους
μαύρες μπάλες. Προφανώς, για οποιουσδήποτε θετικούς ακέραιους  και
και  είναι
είναι  . Έστω
. Έστω  . Ας υποθέσουμε ότι η πρώτη μπάλα που τραβάμε είναι άσπρη. Τότε η διαδικασία μπορεί να ακολουθήσει μια από τις παρακάτω πορείες:
. Ας υποθέσουμε ότι η πρώτη μπάλα που τραβάμε είναι άσπρη. Τότε η διαδικασία μπορεί να ακολουθήσει μια από τις παρακάτω πορείες:
 Οι αντίστοιχες πιθανότητες είναι:
Οι αντίστοιχες πιθανότητες είναι:
Στην τελευταία περίπτωση έχουμε επιλέξει πρώτα όλες τις άσπρες οπότε η διαδικασία τερματίζεται και με πιθανότητα
 η τελευταία μπάλα είναι άσπρη.
η τελευταία μπάλα είναι άσπρη.Αν η πρώτη μπάλα που τραβάμε είναι μαύρη τότε η διαδικασία μπορεί να ακολουθήσει μια από τις παρακάτω πορείες:
 με αντίστοιχες πιθανότητες:
με αντίστοιχες πιθανότητες:
Στην τελευταία περίπτωση έχουμε επιλέξει πρώτα όλες τις μαύρες οπότε η διαδικασία τερματίζεται και με πιθανότητα
 η τελευταία μπάλα είναι άσπρη.
η τελευταία μπάλα είναι άσπρη.Πρώτη περίπτωση (πρώτη μπάλα άσπρη): Έστω ότι έχουμε επιλέξει συνεχόμενα (μετά την πρώτη μπάλα και μέχρι την αλλαγή χρώματος)
 άσπρες μπάλες
άσπρες μπάλες  . Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι
. Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι 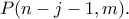
Δεύτερη περίπτωση (πρώτη μπάλα μαύρη): Έστω ότι έχουμε επιλέξει συνεχόμενα (μετά την πρώτη μπάλα και μέχρι την αλλαγή χρώματος)
 μαύρες μπάλες
μαύρες μπάλες 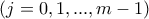 . Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι
. Η διαδικασία μετά ξαναρχίζει και η πιθανότητα να τερματίσουμε σε άσπρη είναι 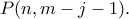
Με βάση την παραπάνω ανάλυση παίρνουμε τελικά την παρακάτω αναγωγική εξίσωση:
![\displaystyle{ P(n,m)=\sum_{j=0}^{n-1}\left [ \prod_{k=0}^{j} \frac{n-k}{n+m-k}\right ] \frac{m}{n+m-j-1} P(n-j-1,m) } \displaystyle{ P(n,m)=\sum_{j=0}^{n-1}\left [ \prod_{k=0}^{j} \frac{n-k}{n+m-k}\right ] \frac{m}{n+m-j-1} P(n-j-1,m) }](/forum/ext/geomar/texintegr/latexrender/pictures/f56aa04d6966bda9301855ff062c8710.png)
![\displaystyle{ +\sum_{j=0}^{m-1}\left [ \prod_{k=0}^{j} \frac{m-k}{n+m-k} \right] \frac{n}{n+m-j-1} \left P(n,m-j-1) } \displaystyle{ +\sum_{j=0}^{m-1}\left [ \prod_{k=0}^{j} \frac{m-k}{n+m-k} \right] \frac{n}{n+m-j-1} \left P(n,m-j-1) }](/forum/ext/geomar/texintegr/latexrender/pictures/faa019a8d9e2a9125045d3fffcd1eee6.png) ή (λίγο) πιο κομψά:
ή (λίγο) πιο κομψά:
 όπου
όπου  και
και 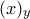 το καθοδικό παραγοντικό
το καθοδικό παραγοντικό  τάξης του
τάξης του  .
.Προχωράμε τώρα με επαγωγή (ισχυρή) για να δείξουμε ότι
 για οποιουσδήποτε θετικούς ακέραιους
για οποιουσδήποτε θετικούς ακέραιους  και
και  . Εύκολα ελέγχουμε ότι
. Εύκολα ελέγχουμε ότι  Θα δείξουμε τώρα ότι:
Θα δείξουμε τώρα ότι: Είναι
Είναι
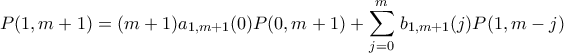
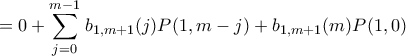

 Όμοια δείχνουμε ότι
Όμοια δείχνουμε ότι  για κάθε
για κάθε  Τελικά, για οποιουσδήποτε θετικούς ακέραιους
Τελικά, για οποιουσδήποτε θετικούς ακέραιους  και
και  είναι
είναι 
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Άσπρες και μαύρες μπάλες
Φαίνεται σωστό αλλά δεν το μελέτησα προσεκτικά. Βάζω μια πιο σύντομη προσέγγιση:
Θα δείξουμε με επαγωγή στο ότι αν έχουμε
ότι αν έχουμε  άσπρες μπάλες και
άσπρες μπάλες και 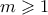 μαύρες μπάλες τότε η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
μαύρες μπάλες τότε η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.
Η επαγωγή ξεκινάει με την περίπτωση η οποία είναι προφανής.
η οποία είναι προφανής.
Για το επαγωγικό βήμα, αν έχουμε άσπρες μπάλες και
άσπρες μπάλες και 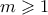 μαύρες μπάλες με
μαύρες μπάλες με  , τότε:
, τότε:
(α) Με πιθανότητα στον πρώτο γύρο (*) αφαιρέσαμε όλες τις άσπρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
στον πρώτο γύρο (*) αφαιρέσαμε όλες τις άσπρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.
(β) Με πιθανότητα στον πρώτο γύρο αφαιρέσαμε όλες τις μαύρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
στον πρώτο γύρο αφαιρέσαμε όλες τις μαύρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.
(γ) Με πιθανότητα μετά το πέρας του πρώτου γύρου εξακολουθούμε να έχουμε και άσπρες και μαύρες μπάλες. Σε αυτήν την περίπτωση, από την επαγωγική υπόθεση, η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
μετά το πέρας του πρώτου γύρου εξακολουθούμε να έχουμε και άσπρες και μαύρες μπάλες. Σε αυτήν την περίπτωση, από την επαγωγική υπόθεση, η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.
Βάζοντάς τα όλα μαζί βλέπουμε ότι η πιθανότητα να καταλήξουμε με άσπρη μπάλα ισούται με

(*) Ο πρώτος γύρος τελειώνει μόλις επιλέξουμε μια μπάλα διαφορετικού χρώματος από την πρώτη μπάλα.
Θα δείξουμε με επαγωγή στο
 ότι αν έχουμε
ότι αν έχουμε  άσπρες μπάλες και
άσπρες μπάλες και 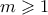 μαύρες μπάλες τότε η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
μαύρες μπάλες τότε η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.Η επαγωγή ξεκινάει με την περίπτωση
 η οποία είναι προφανής.
η οποία είναι προφανής. Για το επαγωγικό βήμα, αν έχουμε
 άσπρες μπάλες και
άσπρες μπάλες και 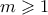 μαύρες μπάλες με
μαύρες μπάλες με  , τότε:
, τότε:(α) Με πιθανότητα
 στον πρώτο γύρο (*) αφαιρέσαμε όλες τις άσπρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
στον πρώτο γύρο (*) αφαιρέσαμε όλες τις άσπρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.(β) Με πιθανότητα
 στον πρώτο γύρο αφαιρέσαμε όλες τις μαύρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
στον πρώτο γύρο αφαιρέσαμε όλες τις μαύρες μπάλες. Σε αυτήν την περίπτωση η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.(γ) Με πιθανότητα
 μετά το πέρας του πρώτου γύρου εξακολουθούμε να έχουμε και άσπρες και μαύρες μπάλες. Σε αυτήν την περίπτωση, από την επαγωγική υπόθεση, η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι
μετά το πέρας του πρώτου γύρου εξακολουθούμε να έχουμε και άσπρες και μαύρες μπάλες. Σε αυτήν την περίπτωση, από την επαγωγική υπόθεση, η πιθανότητα να καταλήξουμε με άσπρη μπάλα είναι  .
.Βάζοντάς τα όλα μαζί βλέπουμε ότι η πιθανότητα να καταλήξουμε με άσπρη μπάλα ισούται με

(*) Ο πρώτος γύρος τελειώνει μόλις επιλέξουμε μια μπάλα διαφορετικού χρώματος από την πρώτη μπάλα.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες
