Κορώνα ή γράμματα
-
Energy Engineer
- Δημοσιεύσεις: 101
- Εγγραφή: Κυρ Μάιος 02, 2010 9:05 pm
- Τοποθεσία: Γερμανία
Κορώνα ή γράμματα
Κάνουμε το εξής πείραμα:
Ρίχνουμε το νόμισμα 100 φορές και μετράμε:
α) Πόσες φορές ήρθε η κορώνα
β) Πόσες φορές ήρθε η πλειοψηφία
Αυτό το κάνουμε άπειρες φορές.
Την πρώτη φορά, η κορώνα ήρθε 53 φορές και η πλειοψηφία (δηλαδή η κορώνα) 53.
Την δεύτερη φορά η κορώνα ήρθε 46 φορές και η πλειοψηφία (δηλαδή τα γράμματα) 54.
Την τρίτη φορά η κορώνα ήρθε 51 φορές και η πλειοψηφία (δηλαδή η κορώνα) 51.
Την τέταρτη φορά η κορώνα ήρθε 50 φορές και η πλειοψηφία 50.
Τα αποτελέσματα των πρώτων 10 φορών του πειράματος:
α) 53, 46, 51, 50, 57, 48, 48, 55, 50, 45, ...
β) 53, 54, 51, 50, 57, 52, 52, 55, 50, 55, ...
Μετά από άπειρες φορές αυτό το πείραμα, ο μέσος όρος του α είναι 50. Ο μέσος όρος του β μετά από άπειρες φορές θα είναι 53.97. Πως αποδεικνύεται;
Ρίχνουμε το νόμισμα 100 φορές και μετράμε:
α) Πόσες φορές ήρθε η κορώνα
β) Πόσες φορές ήρθε η πλειοψηφία
Αυτό το κάνουμε άπειρες φορές.
Την πρώτη φορά, η κορώνα ήρθε 53 φορές και η πλειοψηφία (δηλαδή η κορώνα) 53.
Την δεύτερη φορά η κορώνα ήρθε 46 φορές και η πλειοψηφία (δηλαδή τα γράμματα) 54.
Την τρίτη φορά η κορώνα ήρθε 51 φορές και η πλειοψηφία (δηλαδή η κορώνα) 51.
Την τέταρτη φορά η κορώνα ήρθε 50 φορές και η πλειοψηφία 50.
Τα αποτελέσματα των πρώτων 10 φορών του πειράματος:
α) 53, 46, 51, 50, 57, 48, 48, 55, 50, 45, ...
β) 53, 54, 51, 50, 57, 52, 52, 55, 50, 55, ...
Μετά από άπειρες φορές αυτό το πείραμα, ο μέσος όρος του α είναι 50. Ο μέσος όρος του β μετά από άπειρες φορές θα είναι 53.97. Πως αποδεικνύεται;
Λέξεις Κλειδιά:
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Κορώνα ή γράμματα
Θα το κάνω γενικά για 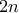 νομίσματα. (Η περίπτωση με
νομίσματα. (Η περίπτωση με  νομίσματα είναι παρόμοια.)
νομίσματα είναι παρόμοια.)
Ας γράψουμε για το πόσα νομίσματα υπάρχουν στην πλειοψηφία. Για
για το πόσα νομίσματα υπάρχουν στην πλειοψηφία. Για 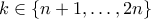 έχουμε
έχουμε
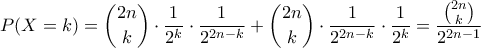
ενώ για έχουμε
έχουμε 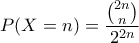
Άρα
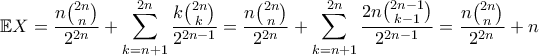
αφού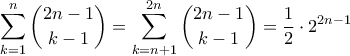
Για νομίσματα (
νομίσματα (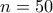 ) έχουμε:
) έχουμε:
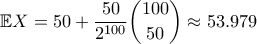
Ας σημειώσουμε επίσης ότι από Stirling
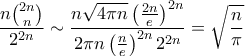
Δηλαδή αναμένουμε ο μέσος όρος της πλειοψηφίας να είναι περίπου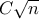 περισσότερος από τα μισά νομίσματα για κάποια σταθερά
περισσότερος από τα μισά νομίσματα για κάποια σταθερά  .
.
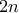 νομίσματα. (Η περίπτωση με
νομίσματα. (Η περίπτωση με  νομίσματα είναι παρόμοια.)
νομίσματα είναι παρόμοια.)Ας γράψουμε
 για το πόσα νομίσματα υπάρχουν στην πλειοψηφία. Για
για το πόσα νομίσματα υπάρχουν στην πλειοψηφία. Για 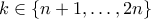 έχουμε
έχουμε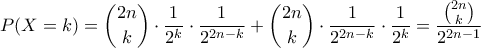
ενώ για
 έχουμε
έχουμε 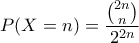
Άρα
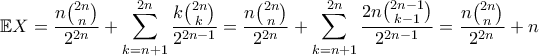
αφού
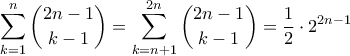
Για
 νομίσματα (
νομίσματα (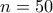 ) έχουμε:
) έχουμε: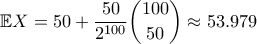
Ας σημειώσουμε επίσης ότι από Stirling
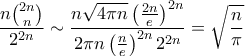
Δηλαδή αναμένουμε ο μέσος όρος της πλειοψηφίας να είναι περίπου
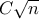 περισσότερος από τα μισά νομίσματα για κάποια σταθερά
περισσότερος από τα μισά νομίσματα για κάποια σταθερά  .
.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
