Μαθηματικά κατεύθυνσης 2014
-
Επιτροπή Θεμάτων 14
- Δημοσιεύσεις: 6
- Εγγραφή: Τρί Μάιος 27, 2014 1:36 am
Μαθηματικά κατεύθυνσης 2014
Αγαπητές/τοί φίλες/οι
Στο θέμα αυτό αποκλειστικά θα συζητήσουμε τα θέματα των Μαθηματικών κατεύθυνσης 2014.
Τα θέματα Μαθηματικών κατεύθυνσης 2014:
Στο θέμα αυτό αποκλειστικά θα συζητήσουμε τα θέματα των Μαθηματικών κατεύθυνσης 2014.
Τα θέματα Μαθηματικών κατεύθυνσης 2014:
Επιτροπή Θεμάτων 2014
- Christos75
- Δημοσιεύσεις: 422
- Εγγραφή: Δευ Φεβ 02, 2009 9:41 pm
- Τοποθεσία: Athens
- Επικοινωνία:
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μαθηματικά κατεύθυνσης 2014
Θέμα Β
α) Έστω ,
,
οπότε

Άρα η εξίσωση έχει λύσεις
β)
γ) ,
,
οπότε ο γεωμετρικός τόπος των εικόνων του είναι ο κύκλος με κέντρο
είναι ο κύκλος με κέντρο  και ακτίνα
και ακτίνα 
α) Έστω
 ,
, οπότε

Άρα η εξίσωση έχει λύσεις

β)

γ)
 ,
, οπότε ο γεωμετρικός τόπος των εικόνων του
 είναι ο κύκλος με κέντρο
είναι ο κύκλος με κέντρο  και ακτίνα
και ακτίνα 
Re: Μαθηματικά κατεύθυνσης 2014
1. Λ
2. Σ
3. Σ
4. Σ
5. Λ
2. Σ
3. Σ
4. Σ
5. Λ
τελευταία επεξεργασία από stavros σε Δευ Ιουν 02, 2014 1:34 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Ωραία θεματάκια επέλεξε η επιτροπή για σήμερα.
Με ξάφνιασε ιδιαίτερα ο ρυθμός μεταβολής, το θέμα το βρήκα χαριτωμένο, ενώ το
το βρήκα χαριτωμένο, ενώ το  βατό.
βατό.
Μου αρέσαν επίσης και τα Σ-Λ
Με ξάφνιασε ιδιαίτερα ο ρυθμός μεταβολής, το θέμα
 το βρήκα χαριτωμένο, ενώ το
το βρήκα χαριτωμένο, ενώ το  βατό.
βατό.Μου αρέσαν επίσης και τα Σ-Λ
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Christos75
- Δημοσιεύσεις: 422
- Εγγραφή: Δευ Φεβ 02, 2009 9:41 pm
- Τοποθεσία: Athens
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Το Θέμα Β ήταν πολύ απλό! Δεν θα έπαιρνε σε έναν υποψήφιο περισσότερο από 12-13' να το ολοκληρώσει! Δεδομένου και του υφιστάμενου άγχους!
Χρήστος Λοΐζος
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Και πάλι δε θα μπορούσα παρά να δώσω συγχαρητήρια στην επιτροπή για την επιλογή των θεμάτων! Διαβαθμισμένα θέματα που καλύπτουν το σύνολο της ύλης και από τα οποία μπορούν να πάρουν μονάδες και οι αδύναμοι μαθητές. Έχει λεπτά σημεία που χρειάζονται δικαιολόγηση αλλά νομίζω ότι χρονικά οι μαθητές μπορούν να προλάβουν να τα γράψουν!
Για μένα είναι ΑΨΟΓΑ τα θέματα!
Λύση του Θέματος Δ
Δ1) άρα η
άρα η  είναι συνεχής στο
είναι συνεχής στο  .
.
Για είναι
είναι  όπου
όπου  . Το πρόσημο της
. Το πρόσημο της  καθορίζει το πρόσημο της
καθορίζει το πρόσημο της  . Η συνάρτηση
. Η συνάρτηση  είναι παραγωγίσιμη σε όλο το
είναι παραγωγίσιμη σε όλο το  με
με  . Επίσης:
. Επίσης:

 άρα η
άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
 άρα η
άρα η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Συνεπώς για έχουμε
έχουμε 
Για έχουμε
έχουμε 
Άρα τελικά αφού η για κάθε
για κάθε  και είναι συνεχής στο
και είναι συνεχής στο  άρα τελικά η
άρα τελικά η  είναι γνησίως αύξουσα σε όλο το
είναι γνησίως αύξουσα σε όλο το  .
.
Δ2) α) Θα βρούμε αρχικά την παράγωγο της στο
στο  με τη χρήση του ορισμού.
με τη χρήση του ορισμού.

άρα η είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  .
.
Τώρα, η είναι προφανής λύση της δοσμένης εξίσωσης αφού για
είναι προφανής λύση της δοσμένης εξίσωσης αφού για  το πρώτο μέλος είναι ίσο με
το πρώτο μέλος είναι ίσο με

Αφού η είναι κυρτή άρα η
είναι κυρτή άρα η  είναι γνησίως αύξουσα συνεπώς:
είναι γνησίως αύξουσα συνεπώς:
για και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε ότι
και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε ότι  για κάθε
για κάθε  . Συνεπώς
. Συνεπώς  άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για
άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για  .
.
Όμοια για και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε και πάλι ότι
και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε και πάλι ότι  . Συνεπώς
. Συνεπώς  άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για
άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για  .
.
Συνεπώς η μοναδική λύση της αρχικής εξίσωσης είναι η .
.
β) Για εκείνα τα για τα οποία
για τα οποία  έχουμε
έχουμε  , συνεπώς
, συνεπώς 
Για ισχύει
ισχύει

Θεωρούμε τη συνάρτηση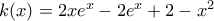 η οποία είναι παραγωγίσιμη στο
η οποία είναι παραγωγίσιμη στο  με
με 

Είναι εύκολο να δούμε με περιπτώσεις ή φτιάχνοντας πίνακα προσήμου ότι για κάθε
για κάθε  .
.
Συνεπώς η είναι γνησίως άυξουσα στο
είναι γνησίως άυξουσα στο  ως συνεχής στο
ως συνεχής στο  . Επίσης η
. Επίσης η  έχει προφανή ρίζα την
έχει προφανή ρίζα την  η οποία είναι και μοναδική. Άρα πρέπει
η οποία είναι και μοναδική. Άρα πρέπει  που απορρίπτεται.
που απορρίπτεται.
Η μόνη περίπτωση που μένει είναι . Τότε
. Τότε και
και  . Άρα τελικά
. Άρα τελικά  οπότε
οπότε  συνεπώς το ζητούμενο σημείο είναι το
συνεπώς το ζητούμενο σημείο είναι το 
Δ3) . Η
. Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  ως γινόμενο παραγωγισίμων με
ως γινόμενο παραγωγισίμων με
 , όπου
, όπου  . Η συνάρτηση
. Η συνάρτηση  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  . Είναι
. Είναι  και
και  άρα η
άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
Μάλιστα επειδή και η
και η  είναι συνεχής στο
είναι συνεχής στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) άρα από το θεώρημα Bolzano υπάρχει
άρα από το θεώρημα Bolzano υπάρχει  ώστε
ώστε  και επειδή η
και επειδή η  είναι γνησίως αύξουσα η ρίζα αυτή είναι μοναδική.
είναι γνησίως αύξουσα η ρίζα αυτή είναι μοναδική.
Τελικά
Συνεπώς φτιάχνοντας ένα πίνακα προσήμου για την φαίνεται εύκολα ότι
φαίνεται εύκολα ότι
 όταν
όταν  ενώ
ενώ  όταν
όταν 
Άρα η είναι γνησίως φθίνουσα σε κάθε ένα από τα διαστήματα
είναι γνησίως φθίνουσα σε κάθε ένα από τα διαστήματα ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) και
και ![[x_0,2] [x_0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/6884c7b8f767e0b6bc529250dc3c18cb.png) ενώ είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα
ενώ είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα ![[1,x_0] [1,x_0]](/forum/ext/geomar/texintegr/latexrender/pictures/f8ff761737c21adc23376b137091d289.png) και
και  .
.
Άρα τελικά όπως φαίνεται και από τον πίνακα μονοτονίας, η έχει
έχει  θέσεις τοπικών ελαχίστων στα
θέσεις τοπικών ελαχίστων στα  και
και  και μία θέση τοπικού μεγίστου στο
και μία θέση τοπικού μεγίστου στο  .
.
Ελπίζω να μην έχω κάνει κάποιο τυπογραφικό την ώρα που τα έγραφα!
Αλέξανδρος
Για μένα είναι ΑΨΟΓΑ τα θέματα!
Λύση του Θέματος Δ
Δ1)
 άρα η
άρα η  είναι συνεχής στο
είναι συνεχής στο  .
.Για
 είναι
είναι  όπου
όπου  . Το πρόσημο της
. Το πρόσημο της  καθορίζει το πρόσημο της
καθορίζει το πρόσημο της  . Η συνάρτηση
. Η συνάρτηση  είναι παραγωγίσιμη σε όλο το
είναι παραγωγίσιμη σε όλο το  με
με  . Επίσης:
. Επίσης:
 άρα η
άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
 άρα η
άρα η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Συνεπώς για
 έχουμε
έχουμε 
Για
 έχουμε
έχουμε 
Άρα τελικά αφού η
 για κάθε
για κάθε  και είναι συνεχής στο
και είναι συνεχής στο  άρα τελικά η
άρα τελικά η  είναι γνησίως αύξουσα σε όλο το
είναι γνησίως αύξουσα σε όλο το  .
.Δ2) α) Θα βρούμε αρχικά την παράγωγο της
 στο
στο  με τη χρήση του ορισμού.
με τη χρήση του ορισμού.
άρα η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  .
.Τώρα, η
 είναι προφανής λύση της δοσμένης εξίσωσης αφού για
είναι προφανής λύση της δοσμένης εξίσωσης αφού για  το πρώτο μέλος είναι ίσο με
το πρώτο μέλος είναι ίσο με 
Αφού η
 είναι κυρτή άρα η
είναι κυρτή άρα η  είναι γνησίως αύξουσα συνεπώς:
είναι γνησίως αύξουσα συνεπώς:για
 και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε ότι
και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε ότι  για κάθε
για κάθε  . Συνεπώς
. Συνεπώς  άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για
άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για  .
.Όμοια για
 και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε και πάλι ότι
και είναι απλό (με διάκριση περιπτώσεων) να δείξουμε και πάλι ότι  . Συνεπώς
. Συνεπώς  άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για
άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για  .
.Συνεπώς η μοναδική λύση της αρχικής εξίσωσης είναι η
 .
.β) Για εκείνα τα
 για τα οποία
για τα οποία  έχουμε
έχουμε  , συνεπώς
, συνεπώς 
Για
 ισχύει
ισχύει 
Θεωρούμε τη συνάρτηση
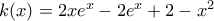 η οποία είναι παραγωγίσιμη στο
η οποία είναι παραγωγίσιμη στο  με
με 

Είναι εύκολο να δούμε με περιπτώσεις ή φτιάχνοντας πίνακα προσήμου ότι
 για κάθε
για κάθε  .
.Συνεπώς η
 είναι γνησίως άυξουσα στο
είναι γνησίως άυξουσα στο  ως συνεχής στο
ως συνεχής στο  . Επίσης η
. Επίσης η  έχει προφανή ρίζα την
έχει προφανή ρίζα την  η οποία είναι και μοναδική. Άρα πρέπει
η οποία είναι και μοναδική. Άρα πρέπει  που απορρίπτεται.
που απορρίπτεται.Η μόνη περίπτωση που μένει είναι
 . Τότε
. Τότε και
και  . Άρα τελικά
. Άρα τελικά  οπότε
οπότε  συνεπώς το ζητούμενο σημείο είναι το
συνεπώς το ζητούμενο σημείο είναι το 
Δ3)
 . Η
. Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  ως γινόμενο παραγωγισίμων με
ως γινόμενο παραγωγισίμων με  , όπου
, όπου  . Η συνάρτηση
. Η συνάρτηση  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  . Είναι
. Είναι  και
και  άρα η
άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
Μάλιστα επειδή
 και η
και η  είναι συνεχής στο
είναι συνεχής στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) άρα από το θεώρημα Bolzano υπάρχει
άρα από το θεώρημα Bolzano υπάρχει  ώστε
ώστε  και επειδή η
και επειδή η  είναι γνησίως αύξουσα η ρίζα αυτή είναι μοναδική.
είναι γνησίως αύξουσα η ρίζα αυτή είναι μοναδική.Τελικά

Συνεπώς φτιάχνοντας ένα πίνακα προσήμου για την
 φαίνεται εύκολα ότι
φαίνεται εύκολα ότι όταν
όταν  ενώ
ενώ  όταν
όταν 
Άρα η
 είναι γνησίως φθίνουσα σε κάθε ένα από τα διαστήματα
είναι γνησίως φθίνουσα σε κάθε ένα από τα διαστήματα ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) και
και ![[x_0,2] [x_0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/6884c7b8f767e0b6bc529250dc3c18cb.png) ενώ είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα
ενώ είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα ![[1,x_0] [1,x_0]](/forum/ext/geomar/texintegr/latexrender/pictures/f8ff761737c21adc23376b137091d289.png) και
και  .
.Άρα τελικά όπως φαίνεται και από τον πίνακα μονοτονίας, η
 έχει
έχει  θέσεις τοπικών ελαχίστων στα
θέσεις τοπικών ελαχίστων στα  και
και  και μία θέση τοπικού μεγίστου στο
και μία θέση τοπικού μεγίστου στο  .
.Ελπίζω να μην έχω κάνει κάποιο τυπογραφικό την ώρα που τα έγραφα!
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Γιάννης Βενιέρης
- Δημοσιεύσεις: 5
- Εγγραφή: Πέμ Μάιος 05, 2011 12:48 pm
Re: Μαθηματικά κατεύθυνσης 2014
Τεράστια η αναντιστοιχία στα θέματα...
Πως είναι δυνατόν να έχουμε τέτοιες αποκλίσεις από χρονιά σε χρονιά;
Πως είναι δυνατόν να έχουμε τέτοιες αποκλίσεις από χρονιά σε χρονιά;
Γιάννης
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μαθηματικά κατεύθυνσης 2014
Για τα Γ1) και Γ2)
Γ1) Η είναι δύο φορές παραγωγίσιμη στο IR με
είναι δύο φορές παραγωγίσιμη στο IR με  και
και
 για κάθε
για κάθε  , οπότε στρέφει τα κοίλα κάτω (κοίλη)
, οπότε στρέφει τα κοίλα κάτω (κοίλη)
Γ2) Η ανίσωση γράφεται ισοδύναμα για κάθε

Αφού η είναι γνήσια αύξουσα στο IR (έχει παράγωγο θετική), είναι
είναι γνήσια αύξουσα στο IR (έχει παράγωγο θετική), είναι

Αφού η είναι γνήσια φθίνουσα, είναι
είναι γνήσια φθίνουσα, είναι 
Γ1) Η
 είναι δύο φορές παραγωγίσιμη στο IR με
είναι δύο φορές παραγωγίσιμη στο IR με  και
και  για κάθε
για κάθε  , οπότε στρέφει τα κοίλα κάτω (κοίλη)
, οπότε στρέφει τα κοίλα κάτω (κοίλη)Γ2) Η ανίσωση γράφεται ισοδύναμα για κάθε


Αφού η
 είναι γνήσια αύξουσα στο IR (έχει παράγωγο θετική), είναι
είναι γνήσια αύξουσα στο IR (έχει παράγωγο θετική), είναι
Αφού η
 είναι γνήσια φθίνουσα, είναι
είναι γνήσια φθίνουσα, είναι 
τελευταία επεξεργασία από Γιώργος Ρίζος σε Δευ Ιουν 02, 2014 12:20 pm, έχει επεξεργασθεί 2 φορές συνολικά.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
- thanasis kopadis
- Δημοσιεύσεις: 149
- Εγγραφή: Παρ Μαρ 22, 2013 9:51 pm
- Τοποθεσία: Πειραιάς - Αττική
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Για άλλη μια φορά η επιτροπή κατάφερε να δώσει πολύ καλή διαβάθμιση στα θέματά της. Θα υπάρχει διασπορά βαθμολογιών, δεδομένου ότι η δυσκολία των θεμάτων κλιμακώνεται σταδιακά.
«Τι είναι το μηδέν, Μπαμπά ;»
«Ο αριθμός των φτερωτών ελεφάντων που στέκονται δίπλα σου.»
«Οι ροζ ή οι άσπροι;»
«Ο αριθμός των φτερωτών ελεφάντων που στέκονται δίπλα σου.»
«Οι ροζ ή οι άσπροι;»
Re: Μαθηματικά κατεύθυνσης 2014
Στο Δ2 α, το γεγονός ότι η  είναι αυστηρά θετική, αποδεικνύεται εύκολα και με εύρεση του συνόλου τιμών. Δηλαδή
είναι αυστηρά θετική, αποδεικνύεται εύκολα και με εύρεση του συνόλου τιμών. Δηλαδή

 είναι αυστηρά θετική, αποδεικνύεται εύκολα και με εύρεση του συνόλου τιμών. Δηλαδή
είναι αυστηρά θετική, αποδεικνύεται εύκολα και με εύρεση του συνόλου τιμών. Δηλαδή
Παντούλας Περικλής
-
Θεοδωρος Παγωνης
- Δημοσιεύσεις: 311
- Εγγραφή: Τετ Οκτ 26, 2011 2:10 pm
- Τοποθεσία: Αγρίνιο
Re: Μαθηματικά κατεύθυνσης 2014
Καλημέρα . Δεν έχει περιορισμό για τοcretanman έγραψε:Και πάλι δε θα μπορούσα παρά να δώσω συγχαρητήρια στην επιτροπή για την επιλογή των θεμάτων! Διαβαθμισμένα θέματα που καλύπτουν το σύνολο της ύλης και από τα οποία μπορούν να πάρουν μονάδες και οι αδύναμοι μαθητές. Έχει λεπτά σημεία που χρειάζονται δικαιολόγηση αλλά νομίζω ότι χρονικά οι μαθητές μπορούν να προλάβουν να τα γράψουν!
Για μένα είναι ΑΨΟΓΑ τα θέματα!
Λύση του Θέματος Δ
Δ1)άρα η
είναι συνεχής στο
.
Γιαείναι
όπου
. Το πρόσημο της
καθορίζει το πρόσημο της
. Η συνάρτηση
είναι παραγωγίσιμη σε όλο το
με
. Επίσης:
άρα η
είναι γνησίως αύξουσα στο
άρα η
είναι γνησίως φθίνουσα στο
Συνεπώς γιαέχουμε
Γιαέχουμε
Άρα τελικά αφού ηγια κάθε
και είναι συνεχής στο
άρα τελικά η
είναι γνησίως αύξουσα σε όλο το
.
Δ2) α) Θα βρούμε αρχικά την παράγωγο τηςστο
με τη χρήση του ορισμού.

άρα ηείναι παραγωγίσιμη στο
με
.
Τώρα, ηείναι προφανής λύση της δοσμένης εξίσωσης αφού για
το πρώτο μέλος είναι ίσο με
Αφού ηείναι κυρτή άρα η
είναι γνησίως αύξουσα συνεπώς:
γιακαι είναι απλό (με διάκριση περιπτώσεων) να δείξουμε ότι
για κάθε
. Συνεπώς
άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για
.
Όμοια γιακαι είναι απλό (με διάκριση περιπτώσεων) να δείξουμε και πάλι ότι
. Συνεπώς
άρα δεν υπάρχουν λύσεις της δοσμένης εξίσωσης για
.
Συνεπώς η μοναδική λύση της αρχικής εξίσωσης είναι η.
β), συνεπώς
Γιαισχύει
Θεωρούμε τη συνάρτησηη οποία είναι παραγωγίσιμη στο
με
Είναι εύκολο να δούμε με περιπτώσεις ή φτιάχνοντας πίνακα προσήμου ότιγια κάθε
.
Συνεπώς ηείναι γνησίως άυξουσα στο
ως συνεχής στο
. Επίσης αφού η
έχει προφανή ρίζα την
η οποία είναι και μοναδική. Συνεπώς η εξίσωση
γράφεται
Άρασυνεπώς το ζητούμενο σημείο είναι το
Δ3). Η
είναι παραγωγίσιμη στο
ως γινόμενο παραγωγισίμων με
, όπου
. Η συνάρτηση
είναι παραγωγίσιμη στο
με
. Είναι
και
άρα η
είναι γνησίως αύξουσα στο
Μάλιστα επειδήκαι η
είναι συνεχής στο
άρα από το θεώρημα Bolzano υπάρχει
ώστε
και επειδή η
είναι γνησίως αύξουσα η ρίζα αυτή είναι μοναδική.
Τελικά
Συνεπώς φτιάχνοντας ένα πίνακα προσήμου για τηνφαίνεται εύκολα ότι
όταν
ενώ
όταν
Άρα ηείναι γνησίως φθίνουσα σε κάθε ένα από τα διαστήματα
και
ενώ είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα
και
.
Άρα τελικά όπως φαίνεται και από τον πίνακα μονοτονίας, ηέχει
θέσεις τοπικών ελαχίστων στα
και
και μία θέση τοπικού μεγίστου στο
.
Ελπίζω να μην έχω κάνει κάποιο τυπογραφικό την ώρα που τα έγραφα!
Αλέξανδρος
 λόγω παρονομαστή;
λόγω παρονομαστή;- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μαθηματικά κατεύθυνσης 2014
Για το Γ3
Είναι
Επειδή υπάρχει το , είναι
, είναι  ,
,
οπότε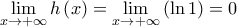 . Η ευθεία
. Η ευθεία  είναι η οριζόντια ασύμπτωτης της
είναι η οριζόντια ασύμπτωτης της  στο
στο 
Είναι
Είναι αφού
αφού 
οπότε
και , οπότε η
, οπότε η  είναι η πλάγια ασύμπτωτη της
είναι η πλάγια ασύμπτωτη της  στο
στο 
Είναι

Επειδή υπάρχει το
 , είναι
, είναι  ,
, οπότε
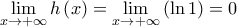 . Η ευθεία
. Η ευθεία  είναι η οριζόντια ασύμπτωτης της
είναι η οριζόντια ασύμπτωτης της  στο
στο 
Είναι

Είναι
 αφού
αφού 
οπότε

και
 , οπότε η
, οπότε η  είναι η πλάγια ασύμπτωτη της
είναι η πλάγια ασύμπτωτη της  στο
στο 
-
Βαγγέλης Κορφιάτης
- Δημοσιεύσεις: 13
- Εγγραφή: Δευ Ιουν 02, 2014 11:19 am
Re: Μαθηματικά κατεύθυνσης 2014
Καλημέρα συνάδελφοι.
Είμαι νέος στο δίκτυο και δεν έχω εξοικειωθεί με το περιβάλλον.
Νομίζω ότι η πρόταση γ στο Α θέμα πρέπει να χαρακτηριστεί λάθος.
Πιθανόν η συνάρτηση να ορίζεται σε μεμονωμένο σημείο στο οποίο να παρουσιάζει το ολικό μέγιστο.
Το ολικό μέγιστο δεν είναι κατ' ανάγκην ούτε το supremum των τοπικών μεγίστων.
Είμαι νέος στο δίκτυο και δεν έχω εξοικειωθεί με το περιβάλλον.
Νομίζω ότι η πρόταση γ στο Α θέμα πρέπει να χαρακτηριστεί λάθος.
Πιθανόν η συνάρτηση να ορίζεται σε μεμονωμένο σημείο στο οποίο να παρουσιάζει το ολικό μέγιστο.
Το ολικό μέγιστο δεν είναι κατ' ανάγκην ούτε το supremum των τοπικών μεγίστων.
- Christos75
- Δημοσιεύσεις: 422
- Εγγραφή: Δευ Φεβ 02, 2009 9:41 pm
- Τοποθεσία: Athens
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
spege έγραψε:το Γ4 δεν μου αρέσει ....ισως να έχει πρόβλημα
Σπύρος
Σαν τι πρόβλημα?
Χρήστος Λοΐζος
- Γιώργος Απόκης
- Διευθύνον Μέλος
- Δημοσιεύσεις: 5092
- Εγγραφή: Δευ Μάιος 16, 2011 7:56 pm
- Τοποθεσία: Πάτρα
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
A.1 Σχολικό βιβλίο, σελίδα 251
A.2 Σχολικό βιβλίο, σελίδα 273
A.3 Σχολικό βιβλίο, σελίδα 150
A.2 Σχολικό βιβλίο, σελίδα 273
A.3 Σχολικό βιβλίο, σελίδα 150
Γιώργος
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά κατεύθυνσης 2014
Θοδωρή έχεις δίκιο και το διόρθωσα.Θεοδωρος Παγωνης έγραψε:Καλημέρα . Δεν έχει περιορισμό για τολόγω παρονομαστή;
Δίνω και μία εναλλακτική λύση για το Δ2 απλούστερη.
Θέλουμε να βρούμε το
 για το οποίο ισχύει
για το οποίο ισχύει  .
.Άρα
 .
.Άρα το ζητούμενο σημείο είναι το

Αλέξανδρος
Αλέξανδρος Συγκελάκης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες

 , η ύπαρξη της ρίζας
, η ύπαρξη της ρίζας  , γίνεται και με
, γίνεται και με 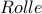 στο
στο ![στο[1,2] στο[1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/e89b66efd11fec471f033fc6ca4fe552.png) για τη συνάρτηση
για τη συνάρτηση