Ναι σωστό είναι, καλό είναι όταν διαίρεσες αριθμητή και παρονομαστή με x να τόνισες ότι είναι διάφορο του 0, καθώς τείνει στο συν άπειρο. Αλλά και να μην το τόνισες είναι προφανές, οπότε πήρες 6 στα 6 μόρια. Καλή συνέχεια!nks έγραψε:Επιτροπή Θεμάτων 16 έγραψε:Δημοσιεύουμε την 1η Έκδοση του Δελτίου Λύσεων τουστη σημερινή εξέταση των μαθητών στα Μαθηματικά που επιμελήθηκαν τα Διευθύνοντα Μέλη του mathematica.
Δόθηκε ιδιαίτερη έμφαση στις εναλλακτικές προσεγγίσεις κάποιων επιμέρους ερωτημάτων με σκοπό τη διευκόλυνση και των συναδέλφων Βαθμολογητών των οποίων το δύσκολο έργο ξεκινά μεθαύριο. Οι εναλλακτικοί τρόποι βρίσκονται στο τέλος του Δελτίου.
Τυχόντα τυπογραφικά/λάθη ή εναλλακτικές προσεγγίσεις σε κάποια ερωτήματα (μόνο αν διαφέρουν στην ουσία της λύσης και όχι στον τρόπο γραφής) μπορείτε να τα στέλνετε με προσωπικό μήνυμα στον παρόντα λογαριασμό είτε με email στο info (AT) mathematica.gr
Ευχόμαστε καλή συνέχεια στους μαθητές μας που διαγωνίστηκαν και καλά αποτελέσματα!
Εκ μέρους της επιτροπής σύνταξης του Δελτίου Λύσεων
Στο Θέμα Δ4 εγώ έδωσα άλλη λύση.
Διαίρεσα αριθμητή και παρονομαστή με x οπότε θα αριθμητής με κριτήριο παρεμβολής είναι 0 και ο παρονομαστής με de l'hospital έβγαλα ότι είναι αριθμός διάφορος του μηδενός γιατί ξέρουμε ότι f'(x)>0.
Δηλαδή τελικά ολόκληρο το όριο κάνει 0.
Δεν είναι σωστό;
Υ.Γ. Εννοείται ότι στον κανόνα DLH πρέπει να τονίσεις ότι έχεις απροσδιοριστία συν άπειρο δια συν άπερο, που απαιτεί πρώτα να έχεις βρεί το όριο της f στο συν άπειρο.

 είναι μοναδική λύση της εξίσωσης.
είναι μοναδική λύση της εξίσωσης.  που να είναι λύση της εξίσωσης. Ισxύει
που να είναι λύση της εξίσωσης. Ισxύει 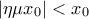 (από τη γνωστή ανισότητα
(από τη γνωστή ανισότητα  με ισότητα μόνο για
με ισότητα μόνο για  και
και 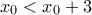 .
. Αν
Αν 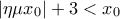 τότε
τότε  και επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα
και επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα ![\left[|\eta\mu x_0|, |\eta\mu x_0|+3\right], \ \left[x_0,x_0+3\right] \left[|\eta\mu x_0|, |\eta\mu x_0|+3\right], \ \left[x_0,x_0+3\right]](/forum/ext/geomar/texintegr/latexrender/pictures/b23bf28fb8af84eff9d273f63a43f50a.png) άρα υπάρxουν
άρα υπάρxουν  ώστε η εξίσωση να γράφεται:
ώστε η εξίσωση να γράφεται: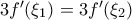 απ΄όπου
απ΄όπου  και αφού η
και αφού η  είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και
είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και  κι έτσι παίρνουμε
κι έτσι παίρνουμε  , πράγμα άτοπο αφού τα
, πράγμα άτοπο αφού τα  ανήκουν σε διαφορετικά διαστήματα.
ανήκουν σε διαφορετικά διαστήματα.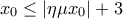 τότε
τότε 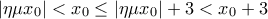 .
. 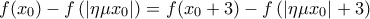
![\left[|\eta\mu x_0|, x_0\right], \ \left[|\eta\mu x_0|+3, x_0+3\right] \left[|\eta\mu x_0|, x_0\right], \ \left[|\eta\mu x_0|+3, x_0+3\right]](/forum/ext/geomar/texintegr/latexrender/pictures/35f56cb0e89ae84a5e44c3c79d576874.png) άρα υπάρxουν
άρα υπάρxουν  ώστε η εξίσωση να γράφεται:
ώστε η εξίσωση να γράφεται: και αφού
και αφού  άρα
άρα  και απο απροσεξία έιδα οτι ήταν
και απο απροσεξία έιδα οτι ήταν  παρασυρόμενος απο αυτή τη βλακεία με λάθος τρόπο απέδειξα ότι η συνάρτηση ήταν η
παρασυρόμενος απο αυτή τη βλακεία με λάθος τρόπο απέδειξα ότι η συνάρτηση ήταν η  και Δ2,Δ3,Δ3 πήγαν κατα διαόλου...σωστά θα ήταν αν είχα αποδείξει με σωστό τρόπο τη συνάρτηση αλλά δε τα κατάφερα και ούτε νομίζω θα τα κατάφερνα αφού ο χρόνος να συλλάβω την ιδέα και να την αποδείξω δε μου έφτανε. Εκει που υπολόγιζα δηλαδή να χάσω απο το Γ2 ( επειδή βρήκα 2 συναρτησεις) και απο το Γ4 επειδη δεν πήρα δευτερη περιπτωση για το ΘΜΤ κατέληξα να πάρω μηδεν σε 3 ερωτηματα...και απο ένα 18 και γιατί όχι και 18,8 που υπολόγιζα είμαι στο 15.5 με το ζόρι..υπάρχει μια περίπτωση να πάρω έστω λίγα μόρια στα 3 αυτά ερωτήματα? φοβάμαι μην ο βαθμολογητής νομίζει οτι πήγα να τον κοροιδέψω με αυτή τη λανθασμένη απόδειξη. τα χειρότερα συμβαίνουν εκεί που δε τα περιμένεις τελικά
και Δ2,Δ3,Δ3 πήγαν κατα διαόλου...σωστά θα ήταν αν είχα αποδείξει με σωστό τρόπο τη συνάρτηση αλλά δε τα κατάφερα και ούτε νομίζω θα τα κατάφερνα αφού ο χρόνος να συλλάβω την ιδέα και να την αποδείξω δε μου έφτανε. Εκει που υπολόγιζα δηλαδή να χάσω απο το Γ2 ( επειδή βρήκα 2 συναρτησεις) και απο το Γ4 επειδη δεν πήρα δευτερη περιπτωση για το ΘΜΤ κατέληξα να πάρω μηδεν σε 3 ερωτηματα...και απο ένα 18 και γιατί όχι και 18,8 που υπολόγιζα είμαι στο 15.5 με το ζόρι..υπάρχει μια περίπτωση να πάρω έστω λίγα μόρια στα 3 αυτά ερωτήματα? φοβάμαι μην ο βαθμολογητής νομίζει οτι πήγα να τον κοροιδέψω με αυτή τη λανθασμένη απόδειξη. τα χειρότερα συμβαίνουν εκεί που δε τα περιμένεις τελικά  μπορείς να πείς ότι ξ1 μικρότερο του ξ2 και θέλει απόδειξη που εδώ δεν νομίζω να είναι ξένα. Αλλιώς το ξ1 δεν μπορείς να πεις ότι είναι μικρότερο από το ξ2, άρα απέδειξες μόνο την ύπαρξη μιας ρίζας, της προφανούς. Θα πάρεις λίγα μόρια, δεν ξέρω πόσα, εγώ θα έδινα 2 στα 9 σίγουρα, μην αρκεστείς σε αυτό ρώτα και τον καθηγητή σου και άλλους συναδέλφους. Καλή συνέχεια!
μπορείς να πείς ότι ξ1 μικρότερο του ξ2 και θέλει απόδειξη που εδώ δεν νομίζω να είναι ξένα. Αλλιώς το ξ1 δεν μπορείς να πεις ότι είναι μικρότερο από το ξ2, άρα απέδειξες μόνο την ύπαρξη μιας ρίζας, της προφανούς. Θα πάρεις λίγα μόρια, δεν ξέρω πόσα, εγώ θα έδινα 2 στα 9 σίγουρα, μην αρκεστείς σε αυτό ρώτα και τον καθηγητή σου και άλλους συναδέλφους. Καλή συνέχεια! και τη σχέση που ισχύει
και τη σχέση που ισχύει  (1).
(1). , τότε
, τότε  για
για  άρα είναι γνήσια φθίνουσα στο διάστημα
άρα είναι γνήσια φθίνουσα στο διάστημα ![(-\propto ,0] (-\propto ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/2270d36a09b2b2c717f9085ed9630bf3.png) .
. , τότε
, τότε  ,
, 
 άτοπο.
άτοπο. , τότε
, τότε  ,
, 
 άτοπο.
άτοπο. . Επειδή ο χρόνος αυτές τις μέρες είναι περιορισμένος και το μυαλό πολύ ταλαιπωρημένο, παρακαλώ τους συναδέλφους να ελέγξουν τις παραπάνω σκέψεις. Αν δεν έχουν κάποιο λάθος, θα το ξανακοιτάξω μήπως καταφέρω να το συμπληρώσω όταν βρω χρόνο!
. Επειδή ο χρόνος αυτές τις μέρες είναι περιορισμένος και το μυαλό πολύ ταλαιπωρημένο, παρακαλώ τους συναδέλφους να ελέγξουν τις παραπάνω σκέψεις. Αν δεν έχουν κάποιο λάθος, θα το ξανακοιτάξω μήπως καταφέρω να το συμπληρώσω όταν βρω χρόνο!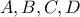 είναι σημεία πάνω στο γράφημα κυρτής συνάρτησης τέτοια ώστε
είναι σημεία πάνω στο γράφημα κυρτής συνάρτησης τέτοια ώστε  ή
ή 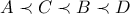 τότε η κλίση του
τότε η κλίση του  είναι μικρότερη της κλίσης του
είναι μικρότερη της κλίσης του  .
. ,
,  ,
, 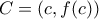 ,
,  , η παραπάνω πρόταση επαναδιατυπώνεται ως εξής:
, η παραπάνω πρόταση επαναδιατυπώνεται ως εξής: είναι κυρτή και αν
είναι κυρτή και αν  ή
ή  τότε
τότε  .
.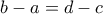 .]
.] , όπου
, όπου  ,
,  . Στην περίπτωση
. Στην περίπτωση  κλίση(
κλίση( )
)  , θεωρούμε την
, θεωρούμε την  , οπότε
, οπότε  , και για τον αριθμητή
, και για τον αριθμητή  ισχύουν οι
ισχύουν οι  ,
,  για
για  , άρα
, άρα  για
για  είναι αύξουσα για
είναι αύξουσα για  . Για την κλίση(
. Για την κλίση( , ενεργούμε ανάλογα, θέτοντας αυτήν την φορά
, ενεργούμε ανάλογα, θέτοντας αυτήν την φορά  , κλπ]
, κλπ] με
με  διαφορετικό του
διαφορετικό του  .
.