Πολύ σωστά συνάδελφε και συγχαρητήρια για την πετυχημένη ανακατασκευή σου! Αν δινόταν η συνάρτηση που βρήκες, οι μαθητές θα είχαν τότε περισσότερη άνεση να σχεδιάσουν το γράφημα χωρίς να το στριμώξουν στο [0, 1) ή να σκεφτούν να αλλάξουν κλίμακα ή ακόμη να προβληματιζονται πως ακριβώς θα τοποθετήσουν ακριβώς τις ρίζες στον άξονα.Μπάμπης Στεργίου έγραψε:Με λίγη περισσότερη επιμονή στην ΚΕΕ, η συνάρτηση (αν δεν έκανα κάποιο βιαστικό λάθος) θα μπορούσε δοθεί ως :Irakleidis έγραψε:Μια παιδαγωγική παρατήρηση στο θέμα Β
Η ζητούμενη γραφική παράσταση στριμώχνεται στο διάστημα [0, 1)
με αποτέλεσμα κάποιοι μαθητές να είχαν πρόβλημα στην επιτυχή διαπραγμάτευση του. Αν όμως δίναμε από την αρχή την συνάρτηση 2f(x) δηλαδή ο τύπος να είχε ένα δυαράκι στον αριθμητή, τότε οι πράξεις απλοποιούνται χωρίς να έχουμε αλλαγή στα ζητούμενα. Η γραφική παράσταση θα είχε τότε οριζόντια ασύμπτωτη την ευθεία y=2 και σημεία καμπής στα σημεία με τετμημένες -1 και 1 αποφεύγοντας έτσι ριζικά. Επιπλέον με ανεβασμένη την ψυχολογία οι μαθητές θα είχαν περισσότερο χρόνο για την διαπραγμάτευση των υπολοίπων θεμάτων.

που δίνει ΣΚ τακαι ασύμπτωτη την
. Και έτσι όμως δεν είναι άσχημα,μια και δεν έχουμε πολύ δύσκολα νούμερα.
Μπ
Μαθηματικά προσαν. (κατεύθ.) 2016
-
Irakleidis
- Δημοσιεύσεις: 5
- Εγγραφή: Παρ Μάιος 20, 2016 4:37 pm
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Χαίρομαι! Φαντάζομαι είσαι μαθητής οπότε μην σε απασχολούν σε πρώτη φάση αρμοδιότητες άλλων. Να έχεις εμπιστοσύνη σε αυτά που γράφεις και σίγουρα η λύση σου θα αξιολογηθεί σωστά! Σίγουρα διάβασες αρκετά σχόλια γύρω από αυτό το θέμα χωρίς να με θέτει πρωτοπόρο στον τρόπο επίλυσης του Γ4 με ΘΜΤ. Ήδη έχει προταθεί ως λύση ίσως όχι ακριβώς έτσι αλλά αρκετά κοντά από τους αξιόλογους συναδέλφους! Δεν υπάρχει λόγος να αναπτυχθεί ο τρόπος βαθμολόγησης γενικά. αλλά έχε εμπιστοσύνη όπως σου είπα στην πολύ καλή προσπάθεια που κάνουν οι συνάδελφοι για να τείνουν οι αξιολογήσεις σε πλήρη αντικειμενικότητα χωρίς την απώλεια και ενός μορίου. Καλή συνέχεια στα υπόλοιπα μαθήματά σου...tzkostas έγραψε:Να ξερετε πως μολις μου ανεβασατε την ψυχολογια με αυτο που ειπατεξιμ έγραψε:Καλησπέρα και συγχαρητήρια για την καταπληκτική δουλειά που κάνετε όλα αυτά τα χρόνια.
Επισυνάπτω το ακόλουθο pdf όπου έχω μια λύση για το Γ.4 με Θ.Μ.Τ αλλά και τη γνώμη μου για την κατανομή μορίων.
Μόρια (Προσωπική Άποψη):
• 1 για την προφανή ρίζα.
• 3+3 για τις δύο περιπτώσεις διαμέρισης.
• 2 χρήση μονοτονίας της παραγώγου από κυρτότητα για την απόδειξη ανισοτήτων.
Θεωρώ δύσκολη αυτή την αντιμετώπιση και από τους καλά διαβασμένους που σκέφτηκαν πιο γενικά την Ανάλυση (ΘΜΤ) και όχι τεχνικά με την θεώρηση συνάρτησης. Οπότε για τους υποψήφιους που κάναν ΘΜΤ θέλω να τους φαντάζομαι βαθμολογικά κοντά στους υποψήφιους που κάναν θεώρηση και σε καμία περίπτωση κοντά σε αυτούς που δεν έκανα καθόλου το Γ.4 ή απλά είπαν ρίζα χ=0. Δ.Κ.Παντως εχω μια απορια σχετικα με την βαθμολογηση των γραπτων.Οι βαθμολογητες πως ακριβως βαθμολογουν? Για παραδειγμα την λυση αυτη(με τα 2 ΘΜΤ) την γνωριζουν ολοι?
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Στο Facebook βρήκα μια κατανοητή και σαφέστατη λύση του θέματος Γ2 των Πανελληνίων Εξετάσεων (18/5/2016) από τον Δάσκαλο Αντώνη Κυριακόπουλο και θεώρησα καλό να τη μοιραστώ μαζί σας. Είναι η εξής:
ΘΕΜΑ Γ2.
Να βρείτε τις συνεχείς συναρτήσεις , έτσι ώστε, για κάθε
, έτσι ώστε, για κάθε  ,να ισχύει:
,να ισχύει:
 .
.
Λύση. Έστω ότι μια συνάρτηση πληροί τις δοσμένες συνθήκες. Βρίσκομαι εύκολα ότι για κάθε
πληροί τις δοσμένες συνθήκες. Βρίσκομαι εύκολα ότι για κάθε  , ισχύει:
, ισχύει:  , με το ίσον μόνο αν x=0. Από την δοσμένη ισότητα, έπεται ότι:
, με το ίσον μόνο αν x=0. Από την δοσμένη ισότητα, έπεται ότι:
( για κάθε )
)![\left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right] \left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ec870db411042199f62cd8ca2e2f4bf4.png)
Η f σε καθένα από τα διαστήματα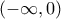 και
και είναι συνεχής και
είναι συνεχής και  και άρα σε καθένα από τα διαστήματα αυτά έχει σταθερό πρόσημο. Θεωρούμε έναν αριθμό από το πρώτο διάστημα, έστω τον
και άρα σε καθένα από τα διαστήματα αυτά έχει σταθερό πρόσημο. Θεωρούμε έναν αριθμό από το πρώτο διάστημα, έστω τον  και έναν αριθμό από το δεύτερο διάστημα, έστω τον 1. Επειδή
και έναν αριθμό από το δεύτερο διάστημα, έστω τον 1. Επειδή και
και , έχουμε τις εξής 4 περιπτώσεις:
, έχουμε τις εξής 4 περιπτώσεις:
1) και
και . Τότε:
. Τότε: , για κάθε
, για κάθε και επειδή
και επειδή , συμπεραίνουμε ότι:
, συμπεραίνουμε ότι:  ,για κάθε
,για κάθε  (1).
(1).
2)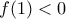 και
και . Τότε:
. Τότε: , για κάθε
, για κάθε και επειδή
και επειδή , συμπεραίνουμε ότι:
, συμπεραίνουμε ότι:  ,για κάθε
,για κάθε  (2).
(2).
3) και
και  .Τότε:
.Τότε:  , για κάθε
, για κάθε και
και  , για κάθε
, για κάθε και επειδή
και επειδή , συμπεραίνουμε ότι:
, συμπεραίνουμε ότι:

4)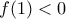 και
και  . Τότε, όπως προηγουμένως βρίσκουμε ότι :
. Τότε, όπως προηγουμένως βρίσκουμε ότι :

Αντιστρόφως. Όπως βρίσκουμε εύκολα, καθεμία από τις 4 συναρτήσεις (1),(2), (3) και (4), πληρούν τις δοσμένες συνθήκες και άρα αυτές είναι οι μοναδικές ζητούμενες.
ΘΕΜΑ Γ2.
Να βρείτε τις συνεχείς συναρτήσεις
 , έτσι ώστε, για κάθε
, έτσι ώστε, για κάθε  ,να ισχύει:
,να ισχύει: .
. Λύση. Έστω ότι μια συνάρτηση
 πληροί τις δοσμένες συνθήκες. Βρίσκομαι εύκολα ότι για κάθε
πληροί τις δοσμένες συνθήκες. Βρίσκομαι εύκολα ότι για κάθε  , ισχύει:
, ισχύει:  , με το ίσον μόνο αν x=0. Από την δοσμένη ισότητα, έπεται ότι:
, με το ίσον μόνο αν x=0. Από την δοσμένη ισότητα, έπεται ότι:( για κάθε
 )
)![\left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right] \left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ec870db411042199f62cd8ca2e2f4bf4.png)
Η f σε καθένα από τα διαστήματα
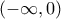 και
και είναι συνεχής και
είναι συνεχής και  και άρα σε καθένα από τα διαστήματα αυτά έχει σταθερό πρόσημο. Θεωρούμε έναν αριθμό από το πρώτο διάστημα, έστω τον
και άρα σε καθένα από τα διαστήματα αυτά έχει σταθερό πρόσημο. Θεωρούμε έναν αριθμό από το πρώτο διάστημα, έστω τον  και έναν αριθμό από το δεύτερο διάστημα, έστω τον 1. Επειδή
και έναν αριθμό από το δεύτερο διάστημα, έστω τον 1. Επειδή και
και , έχουμε τις εξής 4 περιπτώσεις:
, έχουμε τις εξής 4 περιπτώσεις:1)
 και
και . Τότε:
. Τότε: , για κάθε
, για κάθε και επειδή
και επειδή , συμπεραίνουμε ότι:
, συμπεραίνουμε ότι:  ,για κάθε
,για κάθε  (1).
(1).2)
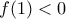 και
και . Τότε:
. Τότε: , για κάθε
, για κάθε και επειδή
και επειδή , συμπεραίνουμε ότι:
, συμπεραίνουμε ότι:  ,για κάθε
,για κάθε  (2).
(2). 3)
 και
και  .Τότε:
.Τότε:  , για κάθε
, για κάθε και
και  , για κάθε
, για κάθε και επειδή
και επειδή , συμπεραίνουμε ότι:
, συμπεραίνουμε ότι:
4)
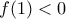 και
και  . Τότε, όπως προηγουμένως βρίσκουμε ότι :
. Τότε, όπως προηγουμένως βρίσκουμε ότι :
Αντιστρόφως. Όπως βρίσκουμε εύκολα, καθεμία από τις 4 συναρτήσεις (1),(2), (3) και (4), πληρούν τις δοσμένες συνθήκες και άρα αυτές είναι οι μοναδικές ζητούμενες.
-
kalafatis_kon
- Δημοσιεύσεις: 135
- Εγγραφή: Πέμ Μαρ 19, 2009 8:49 pm
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Στο συνημμένο αρχείο υπάρχει μιά γεωμετρική προσέγγιση του θέματος Γ2 νομίζω πιό κοντά στην θεωρία του σχολικού που
πατά στην γραφική παράσταση της συνάρτηση |f(x)|. Για την γραφική παράσταση της f αρκεί μόνο να ληφθεί ότι είναι θετική
και έχει ελάχιστο στο μηδέν κάτι που νομίζω έχει βρεθεί στο Γ1.
πατά στην γραφική παράσταση της συνάρτηση |f(x)|. Για την γραφική παράσταση της f αρκεί μόνο να ληφθεί ότι είναι θετική
και έχει ελάχιστο στο μηδέν κάτι που νομίζω έχει βρεθεί στο Γ1.
- Συνημμένα
-
- g2.pdf
- (18.63 KiB) Μεταφορτώθηκε 171 φορές
τελευταία επεξεργασία από kalafatis_kon σε Δευ Μάιος 23, 2016 12:44 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Αγαπητέ συνάδελφε,ghan έγραψε:Στο Facebook βρήκα μια κατανοητή και σαφέστατη λύση του θέματος Γ2 των Πανελληνίων Εξετάσεων (18/5/2016) από τον Δάσκαλο Αντώνη Κυριακόπουλο και θεώρησα καλό να τη μοιραστώ μαζί σας. Είναι η εξής:
ΘΕΜΑ Γ2.
Να βρείτε τις συνεχείς συναρτήσεις, έτσι ώστε, για κάθε
,να ισχύει:
.
Λύση. Έστω ότι μια συνάρτησηπληροί τις δοσμένες συνθήκες. Βρίσκομαι εύκολα ότι για κάθε
, ισχύει:
, με το ίσον μόνο αν x=0. Από την δοσμένη ισότητα, έπεται ότι:
( για κάθε)
![\left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right] \left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ec870db411042199f62cd8ca2e2f4bf4.png)
Η f σε καθένα από τα διαστήματακαι
είναι συνεχής και
και άρα σε καθένα από τα διαστήματα αυτά έχει σταθερό πρόσημο. Θεωρούμε έναν αριθμό από το πρώτο διάστημα, έστω τον
και έναν αριθμό από το δεύτερο διάστημα, έστω τον 1. Επειδή
και
, έχουμε τις εξής 4 περιπτώσεις:
1)και
. Τότε:
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
,για κάθε
(1).
2)και
. Τότε:
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
,για κάθε
(2).
3)και
.Τότε:
, για κάθε
και
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
4)και
. Τότε, όπως προηγουμένως βρίσκουμε ότι :
Αντιστρόφως. Όπως βρίσκουμε εύκολα, καθεμία από τις 4 συναρτήσεις (1),(2), (3) και (4), πληρούν τις δοσμένες συνθήκες και άρα αυτές είναι οι μοναδικές ζητούμενες.
Δε βρίσκω κάτι διαφορετικό στην παραπάνω προσέγγιση σε σχέση με ό,τι έχει γραφτεί μέχρι τώρα σε όλες τις προτεινόμενες λύσεις. Τι εννοεις ότι είναι "κατανοητή και σαφέστατη"; Αφού είναι ακριβώς ίδια με όσες έχουν γραφτεί έως τώρα. Μάλιστα βρίσκω και κάτι περιττό. Είναι η επαλήθευση της οποίας το νόημα δεν αντιλαμβάνομαι.
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Η διαπραγμάτευση με πίνακα προσήμων ανά διάστημα λύνει παραστατικά όχι μόνο την εύρεση , όταν έχουμε μια ρίζα στο β' μέλος , αλλά και περισσότερες.Μας είχε προβληματίσει η παρουσίαση τέτοιων θεμάτων και καταλήξαμε στον βοηθητικό πίνακα που βάλαμε στο βιβλίο. Οι νεότεροι ας ρίξουν μια ματιά στο λυμένο θέμα της εικόνας :ghan έγραψε:Στο Facebook βρήκα μια κατανοητή και σαφέστατη λύση του θέματος Γ2 των Πανελληνίων Εξετάσεων (18/5/2016) από τον Δάσκαλο Αντώνη Κυριακόπουλο και θεώρησα καλό να τη μοιραστώ μαζί σας. Είναι η εξής:
ΘΕΜΑ Γ2.
Να βρείτε τις συνεχείς συναρτήσεις, έτσι ώστε, για κάθε
,να ισχύει:
.
........................................
Μπάμπης
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Αγαπητέ συνάδελφε, καταρχήν η λύση δεν είναι ακριβώς ίδια, όπως γράφεις. Επίσης,cretanman έγραψε: Αγαπητέ συνάδελφε,
Δε βρίσκω κάτι διαφορετικό στην παραπάνω προσέγγιση σε σχέση με ό,τι έχει γραφτεί μέχρι τώρα σε όλες τις προτεινόμενες λύσεις. Τι εννοεις ότι είναι "κατανοητή και σαφέστατη"; Αφού είναι ακριβώς ίδια με όσες έχουν γραφτεί έως τώρα. Μάλιστα βρίσκω και κάτι περιττό. Είναι η επαλήθευση της οποίας το νόημα δεν αντιλαμβάνομαι.
Αλέξανδρος
στο θέμα αυτό ζητάμε να βρούμε τις συναρτήσεις που πληρούν ορισμένες συνθήκες. Σε όλες τις λύσεις που είδα εργάζονται με συνεπαγωγές (τα: έχουμε, επομένως, έτσι κτλ. σημαίνουν συνεπαγωγή), συνεπώς από πουθενά δεν εξασφαλίζεται ότι οι συναρτήσεις που βρίσκουμε πληρούν τις δοσμένες συνθήκες και άρα είναι οι ζητούμενες. Επομένως, η επαλήθευση είναι απαραίτητη για να δούμε ποιες από αυτές που βρήκαμε είναι οι ζητούμενες.
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Αγαπητέ φίλε ghan, η λύση τουghan έγραψε: Επίσης,στο θέμα αυτό ζητάμε να βρούμε τις συναρτήσεις που πληρούν ορισμένες συνθήκες. Σε όλες τις λύσεις που είδα εργάζονται με συνεπαγωγές (τα: έχουμε, επομένως, έτσι κτλ. σημαίνουν συνεπαγωγή), συνεπώς από πουθενά δεν εξασφαλίζεται ότι οι συναρτήσεις που βρίσκουμε πληρούν τις δοσμένες συνθήκες και άρα είναι οι ζητούμενες. Επομένως, η επαλήθευση είναι απαραίτητη για να δούμε ποιες από αυτές που βρήκαμε είναι οι ζητούμενες.
Ο αρχική συνθήκη με τον ποσοδείκτη "Για κάθε πραγματικό
 " αναλύεται στις τέσσερις περιπτώσεις.
" αναλύεται στις τέσσερις περιπτώσεις.Πού κρύβεται η "συνεπαγωγή" που λες; (Ανάλυσε σε παρακαλώ γιατί το "έχουμε" σημαίνει συνεπαγωγή).
Επίσης, αν δεις προσεκτικά την ΑΝΤΙΣΤΟΙΧΗ άσκηση του σχολικού βιβλίου, δουλεύει όπως ακριβώς και στη λύση του
Στο σχολικο βιβλίο ΔΕΝ γίνεται επαλήθευση.
Ειλικρινά τώρα, ισχυρίζεσαι, ότι αν οι μαθητές ακολουθήσουν το Σχολικό βιβλίο θα έχουν κενά στην απάντησή τους;
Παραθέτω την άσκηση του Σχολικού βιβλίου (1.8, Β΄ομ. 7) και τη λύση της με τη θερμή παράκληση να εντοπίσεις αν και που υπάρχει λάθος.
7. i) Έστω
 μια συνεχής συνάρτηση στο διάστημα
μια συνεχής συνάρτηση στο διάστημα ![\displaystyle [ - 1,\,1] \displaystyle [ - 1,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5c6f90f775b4030afe8d7945cb63a378.png) , για την οποία ισχύει
, για την οποία ισχύει για κάθε
για κάθε ![\displaystyle x \in [ - 1,\,1] \displaystyle x \in [ - 1,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/35a4d80ca34508f81e8bfe77861c580d.png) .
.α) Να βρείτε τις ρίζες της εξίσωσης
 .
.β) Να αποδείξετε ότι η
 διατηρεί το πρόσημό της στο διάστημα
διατηρεί το πρόσημό της στο διάστημα  .
.γ) Ποιος μπορεί να είναι ο τύπος της
 και ποια η γραφική της παράσταση;
και ποια η γραφική της παράσταση;ii) Με ανάλογο τρόπο να βρείτε τον τύπο της συνεχούς συνάρτησης
 στο σύνολο
στο σύνολο  , για την οποία ισχύει
, για την οποία ισχύει για κάθε
για κάθε  .
.- Συνημμένα
-
- Pages from 22-0182-02_Mathimatika_G-Lyk-Kat_LYSEIS.pdf
- (221.32 KiB) Μεταφορτώθηκε 166 φορές
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
ghan έγραψε:Στο Facebook βρήκα μια κατανοητή και σαφέστατη λύση του θέματος Γ2 των Πανελληνίων Εξετάσεων (18/5/2016) από τον Δάσκαλο Αντώνη Κυριακόπουλο και θεώρησα καλό να τη μοιραστώ μαζί σας. Είναι η εξής:
ΘΕΜΑ Γ2.
Να βρείτε τις συνεχείς συναρτήσεις, έτσι ώστε, για κάθε
,να ισχύει:
.
Λύση. Έστω ότι μια συνάρτησηπληροί τις δοσμένες συνθήκες. Βρίσκομαι εύκολα ότι για κάθε
, ισχύει:
, με το ίσον μόνο αν x=0. Από την δοσμένη ισότητα, έπεται ότι:
( για κάθε)
![\left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right] \left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ec870db411042199f62cd8ca2e2f4bf4.png)
Η f σε καθένα από τα διαστήματακαι
είναι συνεχής και
και άρα σε καθένα από τα διαστήματα αυτά έχει σταθερό πρόσημο. Θεωρούμε έναν αριθμό από το πρώτο διάστημα, έστω τον
και έναν αριθμό από το δεύτερο διάστημα, έστω τον 1. Επειδή
και
, έχουμε τις εξής 4 περιπτώσεις:
1)και
. Τότε:
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
,για κάθε
(1).
2)και
. Τότε:
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
,για κάθε
(2).
3)και
.Τότε:
, για κάθε
και
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
4)και
. Τότε, όπως προηγουμένως βρίσκουμε ότι :
Αντιστρόφως. Όπως βρίσκουμε εύκολα, καθεμία από τις 4 συναρτήσεις (1),(2), (3) και (4), πληρούν τις δοσμένες συνθήκες και άρα αυτές είναι οι μοναδικές ζητούμενες.
Καλησπέρα. Μήπως γνωρίζετε την αναγκαιότητα της θεώρησης αριθμών σε κάθε διάστημα; Μήπως αυτό πλεονάζει στη λύση;
Και επιπλέον αν είστε σε θέση να μας πληροφορήσετε πόσο χρόνο πήρε η συγκεκριμένη λύση στον συγκεκριμένο λύτη τηρουμένων των αναλογιών πάντοτε με έναν υποψήφιο που πρέπει να απαντήσει και σε άλλα ερωτήματα.
Και τελειώνοντας θα ήθελα να μου πείτε εσείς στις υπόλοιπες λύσεις μας που χρειάζεται επαλήθευση και γιατί.
Φυσικά αν θέλετε. Απλά είχα κάποια ερωτήματα και είπα να τα θέσω.
Ευχαριστώ εκ των προτέρων.
Χρήστος Κυριαζής
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Κύριοι συνάδελφοι.
Όλα τα παραπάνω είναι απόψεις του κυρίου Κυριακόπουλου, ο οποίος με παρακάλεσε να τις αναρτήσω.
Φέρω την ευθύνη γι’ αυτό, αλλά απαντήσεις θα πάρετε μόνο αν έχω κάτι από τον κύριο Κυριακόπουλο.
Όλα τα παραπάνω είναι απόψεις του κυρίου Κυριακόπουλου, ο οποίος με παρακάλεσε να τις αναρτήσω.
Φέρω την ευθύνη γι’ αυτό, αλλά απαντήσεις θα πάρετε μόνο αν έχω κάτι από τον κύριο Κυριακόπουλο.
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
ghan έγραψε:Κύριοι συνάδελφοι.
Όλα τα παραπάνω είναι απόψεις του κυρίου Κυριακόπουλου, ο οποίος με παρακάλεσε να τις αναρτήσω.
Φέρω την ευθύνη γι’ αυτό, αλλά απαντήσεις θα πάρετε μόνο αν έχω κάτι από τον κύριο Κυριακόπουλο.
Αγαπητέ συνάδελφε ghan. (Σε εσένα απευθύνομαι).
Όπως σε κάθε μαθηματική πρόταση, έτσι κι εδώ είναι απαραίτητος ο ποσοδείκτης στην αρχή της πρότασης. Εν προκειμένω ο υπαρξιακός.
Παρακαλώ πολύ, άλλη φορά, καθόριζε στην αρχή της ανάρτησης σου ποιος είσαι ή τίνος την άποψη μάς κοινοποιείς.
Οι απαξιωτικές γενικεύσεις:
"Σε όλες τις λύσεις που είδα (ποιες είναι αυτές;) εργάζονται (ποιοι;) με συνεπαγωγές (τα: έχουμε, επομένως, έτσι κτλ. σημαίνουν συνεπαγωγή), συνεπώς από πουθενά δεν εξασφαλίζεται ότι οι συναρτήσεις που βρίσκουμε πληρούν τις δοσμένες συνθήκες και άρα είναι οι ζητούμενες",
σχετικά με την πληρότητα των λύσεων (και αυτής που αναρτήσαμε εδώ, αλλά και του ίδιου του Σχολικού βιβλίου) αν και τις θεωρώ απαράδεκτες και προσβλητικές, θα έμεναν αναπάντητες,
αν αυτή η διασπορά ανυπόστατων αμφιβολιών δεν εμφανιζόταν εν μέσω βαθμολόγησης γραπτών στα εξεταστικά κέντρα. Δυστυχώς το έργο το έχουμε ξαναδεί και ειλικρινά δεν κατανοώ γιατί επανέρχεται.
- Christos.N
- Δημοσιεύσεις: 2105
- Εγγραφή: Πέμ Νοέμ 26, 2009 2:28 pm
- Τοποθεσία: Ίλιον
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Απευθύνω έκκληση στους συντονιστές, κλειδώστε τον φάκελο όσο το παιδιά δίνουν ακόμα εξετάσεις.
Τα βαθμολογικά κέντρα λειτουργούν άψογα, δημοκρατικά και υπεύθυνα. Οι βαθμολογητές γνωρίζουν ότι εξετάσεις δίνουν τα παιδιά τους σκύβουν από πάνω σε κάθε ερώτημα και η συνεργασία είναι δεδομένη. Ψήγματα μαθηματικής ορθότητας και διαίσθησης να υπάρχουν πηγαίνουν όλα υπέρ του μαθητή. Ας αφήσουμε τις εξετάσεις να κυλήσουν ήρεμα όπως πρέπει και να μην φορτίζουμε επιπλέον αυτό που ήδη είναι γεμάτο από φορτίο.
Συνεχίζουμε οποιαδήποτε κουβέντα και οποιονδήποτε σχολιασμό μετά που θα έχουμε και τα στατιστικά και καθαρό μυαλό όλοι μας. Με πολύ γνωστό μέλος σήμερα του (που χαίρομαι απίστευτα για αυτό ) είχαμε κουβέντα μισή ώρα στο βαθμολογικό 4 άνθρωποι για ένα μόριο, ναι για ένα μόριο. Θέλω να πω ότι προσπαθούμε όχι απλά να μην αδικήσουμε κανέναν αλλά να γίνουμε σοφότεροι στο πως θα διδάσκουμε το μάθημα από εδώ και πέρα κάνοντας αυτοκριτική στο τι κάνουμε ως τώρα. Ούτε εγωισμοί υπάρχουν , ούτε βερμπαλισμοί μόνο γνήσιος παιδαγωγικός και επιστημονικός διάλογος, τους οποίους εύχομαι να οικοδομηθούν και να συνεχιστούν την επαύριο και όχι στην δεδομένη χρονική στιγμή.
(που χαίρομαι απίστευτα για αυτό ) είχαμε κουβέντα μισή ώρα στο βαθμολογικό 4 άνθρωποι για ένα μόριο, ναι για ένα μόριο. Θέλω να πω ότι προσπαθούμε όχι απλά να μην αδικήσουμε κανέναν αλλά να γίνουμε σοφότεροι στο πως θα διδάσκουμε το μάθημα από εδώ και πέρα κάνοντας αυτοκριτική στο τι κάνουμε ως τώρα. Ούτε εγωισμοί υπάρχουν , ούτε βερμπαλισμοί μόνο γνήσιος παιδαγωγικός και επιστημονικός διάλογος, τους οποίους εύχομαι να οικοδομηθούν και να συνεχιστούν την επαύριο και όχι στην δεδομένη χρονική στιγμή.
Συνεπώς υπενθυμίζω την πρόταση μου " κλειδώστε τον φάκελο όσο το παιδιά δίνουν ακόμα εξετάσεις" και του χρόνου να ακολουθήσουμε πιο αυστηρή πολιτική ως και ο φάκελος να μένει ξεκλείδωτος τρεις μέρες μόνο.
και ο φάκελος να μένει ξεκλείδωτος τρεις μέρες μόνο.
Λοιπόν εύχομαι σε όλους τους μαθητές μας στους δασκάλους τους υγεία και καλή δύναμη και στην μαθηματική εκπαίδευση ένα καλύτερο και πιο γόνιμο έδαφος.
στους δασκάλους τους υγεία και καλή δύναμη και στην μαθηματική εκπαίδευση ένα καλύτερο και πιο γόνιμο έδαφος.
Τα βαθμολογικά κέντρα λειτουργούν άψογα, δημοκρατικά και υπεύθυνα. Οι βαθμολογητές γνωρίζουν ότι εξετάσεις δίνουν τα παιδιά τους σκύβουν από πάνω σε κάθε ερώτημα και η συνεργασία είναι δεδομένη. Ψήγματα μαθηματικής ορθότητας και διαίσθησης να υπάρχουν πηγαίνουν όλα υπέρ του μαθητή. Ας αφήσουμε τις εξετάσεις να κυλήσουν ήρεμα όπως πρέπει και να μην φορτίζουμε επιπλέον αυτό που ήδη είναι γεμάτο από φορτίο.
Συνεχίζουμε οποιαδήποτε κουβέντα και οποιονδήποτε σχολιασμό μετά που θα έχουμε και τα στατιστικά και καθαρό μυαλό όλοι μας. Με πολύ γνωστό μέλος σήμερα του
Συνεπώς υπενθυμίζω την πρόταση μου " κλειδώστε τον φάκελο όσο το παιδιά δίνουν ακόμα εξετάσεις" και του χρόνου να ακολουθήσουμε πιο αυστηρή πολιτική ως
Λοιπόν εύχομαι σε όλους τους μαθητές μας
Χρήστος Ντάβας
Wir müssen wissen — wir werden wissen! D.Hilbert
Wir müssen wissen — wir werden wissen! D.Hilbert
- nsmavrogiannis
- Επιμελητής
- Δημοσιεύσεις: 4455
- Εγγραφή: Σάβ Δεκ 20, 2008 7:13 pm
- Τοποθεσία: Αθήνα
- Επικοινωνία:
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
ghan έγραψε: Στο Facebook βρήκα μια κατανοητή και σαφέστατη λύση του θέματος Γ2 των Πανελληνίων Εξετάσεων (18/5/2016) από τον Δάσκαλο Αντώνη Κυριακόπουλο και θεώρησα καλό να τη μοιραστώ μαζί σας. Είναι η εξής:[/color]
ΘΕΜΑ Γ2.
Να βρείτε τις συνεχείς συναρτήσεις, έτσι ώστε, για κάθε
,να ισχύει:
.
Λύση. Έστω ότι μια συνάρτησηπληροί τις δοσμένες συνθήκες. Βρίσκομαι εύκολα ότι για κάθε
, ισχύει:
, με το ίσον μόνο αν x=0. Από την δοσμένη ισότητα, έπεται ότι:
( για κάθε)
![\left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right] \left[ f(x)={{e}^{{{x}^{2}}}}-{{x}^{2}}-1\text{ }f(x)=-\left( {{e}^{{{x}^{2}}}}-{{x}^{2}}-1 \right)\text{ } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ec870db411042199f62cd8ca2e2f4bf4.png)
Η f σε καθένα από τα διαστήματακαι
είναι συνεχής και
και άρα σε καθένα από τα διαστήματα αυτά έχει σταθερό πρόσημο. Θεωρούμε έναν αριθμό από το πρώτο διάστημα, έστω τον
και έναν αριθμό από το δεύτερο διάστημα, έστω τον 1. Επειδή
και
, έχουμε τις εξής 4 περιπτώσεις:
1)και
. Τότε:
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
,για κάθε
(1).
2)και
. Τότε:
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
,για κάθε
(2).
3)και
.Τότε:
, για κάθε
και
, για κάθε
και επειδή
, συμπεραίνουμε ότι:
4)και
. Τότε, όπως προηγουμένως βρίσκουμε ότι :
Αντιστρόφως. Όπως βρίσκουμε εύκολα, καθεμία από τις 4 συναρτήσεις (1),(2), (3) και (4), πληρούν τις δοσμένες συνθήκες και άρα αυτές είναι οι μοναδικές ζητούμενες.
Νισάφι πια:ghan έγραψε:Κύριοι συνάδελφοι.
Όλα τα παραπάνω είναι απόψεις του κυρίου Κυριακόπουλου, ο οποίος με παρακάλεσε να τις αναρτήσω.
Φέρω την ευθύνη γι’ αυτό, αλλά απαντήσεις θα πάρετε μόνο αν έχω κάτι από τον κύριο Κυριακόπουλο.
α) Με το χιλιοειπωμένο τροπάριο για τις ισοδυναμίες. Ποιός κανει ή γράφει έτσι Μαθηματικά;
β) Με τις "υπερ τρίτων" αναρτήσεις. 'Οποιος θεωρεί κάτι αξιόλογο ας μπει στον κόπο και να το υποστηρίξει και ας μην παραπέμπει τους συνομιλητές του αλλού. Το
Πράγματι ουδείς θα ασχολείτο με την ανάρτηση και την συνακόλουθη απαξίωση των λύσεων που έδωσαν στοΓιώργος Ρίζος έγραψε: Οι απαξιωτικές γενικεύσεις: ..
"Σε όλες τις λύσεις που είδα (ποιες είναι αυτές;) εργάζονται (ποιοι;) με συνεπαγωγές (τα: έχουμε, επομένως, έτσι κτλ. σημαίνουν συνεπαγωγή), συνεπώς από πουθενά δεν εξασφαλίζεται ότι οι συναρτήσεις που βρίσκουμε πληρούν τις δοσμένες συνθήκες και άρα είναι οι ζητούμενες", σχετικά με την πληρότητα των λύσεων (και αυτής που αναρτήσαμε εδώ, αλλά και του ίδιου του Σχολικού βιβλίου) αν και τις θεωρώ απαράδεκτες και προσβλητικές, θα έμεναν αναπάντητες,
αν αυτή η διασπορά ανυπόστατων αμφιβολιών δεν εμφανιζόταν εν μέσω βαθμολόγησης γραπτών στα εξεταστικά κέντρα. Δυστυχώς το έργο το έχουμε ξαναδεί και ειλικρινά δεν κατανοώ γιατί επανέρχεται.
Μαυρογιάννης
Αν κανείς δεν ελπίζει, δεν θα βρεί το ανέλπιστο, οι δρόμοι για το ανεξερεύνητο θα είναι κλειστοί.
Ηράκλειτος
Ηράκλειτος
-
Μιχάλης Τσουρακάκης
- Δημοσιεύσεις: 2770
- Εγγραφή: Παρ Ιαν 11, 2013 4:17 am
- Τοποθεσία: Ηράκλειο Κρήτης
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
γράφω μια λύση ακόμη για το  που δεν έχω συναντήσει..
που δεν έχω συναντήσει..
Από την για κάθε x στο
για κάθε x στο  κι επειδή τα δυο μέλη είναι παραγωγίσιμες συναρτήσεις παίρνουμε
κι επειδή τα δυο μέλη είναι παραγωγίσιμες συναρτήσεις παίρνουμε
![\displaystyle{f'(x)\left[ {{e^{f(x)}} - f'(f(x)} \right] = {e^x} - 1 \ne 0} \displaystyle{f'(x)\left[ {{e^{f(x)}} - f'(f(x)} \right] = {e^x} - 1 \ne 0}](/forum/ext/geomar/texintegr/latexrender/pictures/87cf48720e96503afea03a44b1c7ed5c.png) για κάθε x στο
για κάθε x στο 
Άρα στα
στα  ,
,  κι επειδή
κι επειδή  συνεχής θα διατηρεί σταθερό πρόσημο σε καθ ένα από τα παραπάνω διαστήματα
συνεχής θα διατηρεί σταθερό πρόσημο σε καθ ένα από τα παραπάνω διαστήματα
Είναι συνεχής στο
συνεχής στο  οπότε
οπότε 

Άρα υπάρχει ώστε στα
ώστε στα  είναι
είναι  .Άρα
.Άρα  για κάθε
για κάθε  .Έτσι
.Έτσι  δεν παρουσιάζει τ.ακρότατα και είναι γνήσια αύξουσα
δεν παρουσιάζει τ.ακρότατα και είναι γνήσια αύξουσα
 που δεν έχω συναντήσει..
που δεν έχω συναντήσει..Από την
 για κάθε x στο
για κάθε x στο  κι επειδή τα δυο μέλη είναι παραγωγίσιμες συναρτήσεις παίρνουμε
κι επειδή τα δυο μέλη είναι παραγωγίσιμες συναρτήσεις παίρνουμε ![\displaystyle{f'(x)\left[ {{e^{f(x)}} - f'(f(x)} \right] = {e^x} - 1 \ne 0} \displaystyle{f'(x)\left[ {{e^{f(x)}} - f'(f(x)} \right] = {e^x} - 1 \ne 0}](/forum/ext/geomar/texintegr/latexrender/pictures/87cf48720e96503afea03a44b1c7ed5c.png) για κάθε x στο
για κάθε x στο 
Άρα
 στα
στα  ,
,  κι επειδή
κι επειδή  συνεχής θα διατηρεί σταθερό πρόσημο σε καθ ένα από τα παραπάνω διαστήματα
συνεχής θα διατηρεί σταθερό πρόσημο σε καθ ένα από τα παραπάνω διαστήματαΕίναι
 συνεχής στο
συνεχής στο  οπότε
οπότε 

Άρα υπάρχει
 ώστε στα
ώστε στα  είναι
είναι  .Άρα
.Άρα  για κάθε
για κάθε  .Έτσι
.Έτσι  δεν παρουσιάζει τ.ακρότατα και είναι γνήσια αύξουσα
δεν παρουσιάζει τ.ακρότατα και είναι γνήσια αύξουσα- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Ωραίο Μιχάλη!Μιχάλης Τσουρακάκης έγραψε:γράφω μια λύση ακόμη για τοπου δεν έχω συναντήσει..
Από τηνγια κάθε x στο
κι επειδή τα δυο μέλη είναι παραγωγίσιμες συναρτήσεις παίρνουμε
για κάθε x στο
Άραστα
,
κι επειδή
συνεχής θα διατηρεί σταθερό πρόσημο σε καθ ένα από τα παραπάνω διαστήματα
Είναισυνεχής στο
οπότε
Άρα υπάρχειώστε στα
είναι
.Άρα
για κάθε
.Έτσι
δεν παρουσιάζει τ.ακρότατα και είναι γνήσια αύξουσα
Αλέξανδρος Συγκελάκης
-
tsakalanapaka
- Δημοσιεύσεις: 38
- Εγγραφή: Πέμ Απρ 11, 2013 3:02 am
- Τοποθεσία: Ρέθυμνο
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Το μόνο διαφορετικό που έχει είναι οτι είναι λίγο πιο μπερδεμένη για τον μέσο μαθητή.ghan έγραψε:Στο Facebook βρήκα μια κατανοητή και σαφέστατη λύση του θέματος Γ2 των Πανελληνίων Εξετάσεων (18/5/2016) από τον Δάσκαλο Αντώνη Κυριακόπουλο και θεώρησα καλό να τη μοιραστώ μαζί σας. Είναι η εξής:
Αα και οτι δημοσιεύθηκε μια ή δυο μέρες (δεν θυμάμαι ακριβώς) μετά την εξέταση. Μάλλον το να λάβουμε
τυχαίους αριθμούς σε κάθε διάστημα και να κάνουμε επαλήθευση είναι βαθυστόχαστη σκέψη που απαιτεί χρόνο...
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Καθώς δεν είχε κάποιο σχολιασμό από τους συναδέλφους δημόσια ώστε να μην "θαφτεί" το επισυνάπτω σε εσάς κύριε Παύλο Μαραγκουδάκη ως απάντηση αλλά και υλοποίηση και της δική σας ιδέας!Παύλος Μαραγκουδάκης έγραψε:ΑνCoxs έγραψε:ξέρουμε αν το Γ4 βγαίνει με ΘΜΤ στα [|ημχ|,χ],[|ημχ|+3,χ+3] ????τότε μπορούμε να δείξουμε εφαρμόζοντας το ΘΜΤ στα διαστήματα που αναφέρεις, ότι η εξίσωση που δίνεται, είναι αδύνατη.
Αν όμωςτότε τα διαστήματα αυτά δεν είναι ξένα μεταξύ τους και δεν προκύπτει το συμπέρασμα. Αν δουλέψουμε με ΘΜΤ στα διαστήματα
και
τότε αυτά είναι ξένα μεταξύ τους και προκύπτει ότι η εξίσωση είναι αδύνατη και σε αυτήν την περίπτωση.
Λύνεται λοιπόν και με το ΘΜΤ, αρκεί να διακρίνουμε περιπτώσεις.
Επισυνάπτω το ακόλουθο pdf όπου έχω μια λύση για το Γ.4 με Θ.Μ.Τ αλλά και τη γνώμη μου για την κατανομή μορίων.
Μόρια (Προσωπική Άποψη):
• 1 για την προφανή ρίζα.
• 3+3 για τις δύο περιπτώσεις διαμέρισης.
• 2 χρήση μονοτονίας της παραγώγου από κυρτότητα για την απόδειξη ανισοτήτων.
Θεωρώ δύσκολη αυτή την αντιμετώπιση και από τους καλά διαβασμένους που σκέφτηκαν πιο γενικά την Ανάλυση (ΘΜΤ) και όχι τεχνικά με την θεώρηση συνάρτησης. Οπότε για τους υποψήφιους που κάναν ΘΜΤ θέλω να τους φαντάζομαι βαθμολογικά κοντά στους υποψήφιους που κάναν θεώρηση και σε καμία περίπτωση κοντά σε αυτούς που δεν έκανα καθόλου το Γ.4 ή απλά είπαν ρίζα χ=0.
- Kostas Tzimoulias
- Δημοσιεύσεις: 308
- Εγγραφή: Τετ Μαρ 26, 2014 9:50 pm
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
αλήθεια πόσο βαθμολογείται η προφανής ρίζα και το ένα ΘΜΤ..;
“Somewhere, something incredible is waiting to be known...”
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
Η δική μου άποψη όπως έγραψα είναι ότι με το ένα ΘΜΤ λύνει ο μαθητής το "μισό" πρόβλημα διαμέρισης το οποίο ήταν λογικό να μην σκεφτεί την πολύ δύσκολη διαμέριση γύρω από την ρίζα της μη γραμμικής εξίσωσης όπως αναλύω στη λύση μου παραπάνω. Άρα θεωρώ κόστος μορίων max 3 από τα 9! Άρα θα πρέπει να βαθμολογηθεί τουλάχιστον 6/9!Kostas Tzimoulias έγραψε:αλήθεια πόσο βαθμολογείται η προφανής ρίζα και το ένα ΘΜΤ..;
- Kostas Tzimoulias
- Δημοσιεύσεις: 308
- Εγγραφή: Τετ Μαρ 26, 2014 9:50 pm
Re: Μαθηματικά προσαν. (κατεύθ.) 2016
μακάρι...και γω την ώρα του γραπτου δεν είδα το πολύ προφανές θέσιμο συνάρτησής και προσπάθησα να το πάω σε άτοπο με ένα , δυστυχώς , ΘΜΤ απλά το θέμα ειναι οτι στο τέλος είπα αντί για <<άτοπο>> η ισότητα ισχύει μόνο αν ταυτίζονται τα διαστηματα ή κατι τετοιο δε θυμαμαι καλά που αυτό γινόταν για χ=0 μόνο. Τωρα η δικαιολογηση ειναι προβληματικη φαντάζομαι έχω ελπίδες να πάρω ένα έστω 4-5/9?
“Somewhere, something incredible is waiting to be known...”
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες
