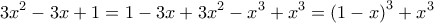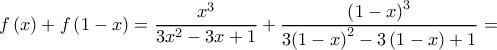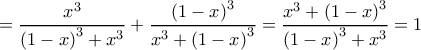Θέματα επαναληπτικών στα Μαθηματικά
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Θέματα επαναληπτικών στα Μαθηματικά
(Δεν γράφω σε latex γιατί προφανώς ο ιστότοπός μας έχει σήμερα κάποιο τεχνικό πρόβλημα και δεν το δέχεται. Το παρατήρησα και το πρωί. Ας το κοιτάξουν οι φίλοι μας Διαχειριστές. Θα επαναφέρω το latex μετά την διόρθωση του προβλήματος.)
Στην Άσκηση Γ1 βλέπω κάποιο θεματάκι. Μάλλον τους ξέφυγε κάτι. Θέλω να πω:
Ολοκληρώνοντας την δοθείσα βρίσκουμε f^2(x)= x+c , που με χρήση του σημείου Μ(1,1) διαπιστώνουμε ότι c=0. Οπότε f^2(x)=x και άρα για κάθε x χωριστά έχουμε πρόσημο (που εξαρτάται από το x) με f(x)=\pm \sqrt x. Αρχικά, μόνο στο x=1 έχουμε την σιγουριά του +.
Για να μπορέσουμε να πούμε ότι παίρνουμε μόνο το + (παντού) χρειάζεται ένα επιχείρημα συνέχειας. Σίγουρα η αξία του ως μέρους μιας επιστημονικά τεκμηριωμένης απάντησης αξίζει περισσότερο από τις 6 μονάδες που δίνει ο θεματοθέτης. Ξέφυγε άραγε αυτό το σημείο από τον εξεταστή; Πήρε το + σε όλα τα σημεία εργαζόμενος διαισθητικά;
Θα ήθελα να έβλεπα μία απόδειξη εντός των 6 μονάδων.
Ομολογώ ότι δεν ξέρω/δεν θυμάμαι αν υπάρχει έτοιμη αιτιολόγηση αυτού του σημείου στο βιβλίο, οπότε είμαστε εντάξει. Αλλιώς ...
Στην Άσκηση Γ1 βλέπω κάποιο θεματάκι. Μάλλον τους ξέφυγε κάτι. Θέλω να πω:
Ολοκληρώνοντας την δοθείσα βρίσκουμε f^2(x)= x+c , που με χρήση του σημείου Μ(1,1) διαπιστώνουμε ότι c=0. Οπότε f^2(x)=x και άρα για κάθε x χωριστά έχουμε πρόσημο (που εξαρτάται από το x) με f(x)=\pm \sqrt x. Αρχικά, μόνο στο x=1 έχουμε την σιγουριά του +.
Για να μπορέσουμε να πούμε ότι παίρνουμε μόνο το + (παντού) χρειάζεται ένα επιχείρημα συνέχειας. Σίγουρα η αξία του ως μέρους μιας επιστημονικά τεκμηριωμένης απάντησης αξίζει περισσότερο από τις 6 μονάδες που δίνει ο θεματοθέτης. Ξέφυγε άραγε αυτό το σημείο από τον εξεταστή; Πήρε το + σε όλα τα σημεία εργαζόμενος διαισθητικά;
Θα ήθελα να έβλεπα μία απόδειξη εντός των 6 μονάδων.
Ομολογώ ότι δεν ξέρω/δεν θυμάμαι αν υπάρχει έτοιμη αιτιολόγηση αυτού του σημείου στο βιβλίο, οπότε είμαστε εντάξει. Αλλιώς ...
-
Kostas2001
- Δημοσιεύσεις: 3
- Εγγραφή: Κυρ Αύγ 25, 2019 1:05 pm
Re: Θέματα επαναληπτικών στα Μαθηματικά
Σας παραθέτω την δική μου λύση του Δ θέματος, καθώς μόλις αποφοίτησα απο τη Γ Λυκείου και μου φάνηκε αρκετά ενδιαφέρον. Οι λύσεις είναι γραπτές αλλά νομίζω οι εικόνες και η γραφή μου είναι καθαρές.
Σας ευχαριστώ.
Σας ευχαριστώ.
τελευταία επεξεργασία από Demetres σε Πέμ Σεπ 05, 2019 8:43 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: Διαγραφή συνδέσμων εικόνας
Λόγος: Διαγραφή συνδέσμων εικόνας
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Θέματα επαναληπτικών στα Μαθηματικά
Εύγε !!! Καλές σπουδές !!!Kostas2001 έγραψε: ↑Τετ Σεπ 04, 2019 9:17 pmΣας παραθέτω την δική μου λύση του Δ θέματος, καθώς μόλις αποφοίτησα απο τη Γ Λυκείου και μου φάνηκε αρκετά ενδιαφέρον. Οι λύσεις είναι γραπτές αλλά νομίζω οι εικόνες και η γραφή μου είναι καθαρές.
Σας ευχαριστώ.
τελευταία επεξεργασία από Demetres σε Πέμ Σεπ 05, 2019 8:44 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: Διαγραφή συνδέσμων εικόνας από παράθεση
Λόγος: Διαγραφή συνδέσμων εικόνας από παράθεση
-
Apo.Antonis
- Δημοσιεύσεις: 21
- Εγγραφή: Δευ Απρ 02, 2018 9:52 am
Re: Θέματα επαναληπτικών στα Μαθηματικά
Δεν μπορούμε να ολοκληρώσουμε καθώς το αόριστο ολοκλήρωμα είναι εκτός ύλης.Mihalis_Lambrou έγραψε: ↑Τετ Σεπ 04, 2019 9:10 pm(Δεν γράφω σε latex γιατί προφανώς ο ιστότοπός μας έχει σήμερα κάποιο τεχνικό πρόβλημα και δεν το δέχεται. Το παρατήρησα και το πρωί. Ας το κοιτάξουν οι φίλοι μας Διαχειριστές. Θα επαναφέρω το latex μετά την διόρθωση του προβλήματος.)
Στην Άσκηση Γ1 βλέπω κάποιο θεματάκι. Μάλλον τους ξέφυγε κάτι. Θέλω να πω:
Ολοκληρώνοντας την δοθείσα βρίσκουμε f^2(x)= x+c , που με χρήση του σημείου Μ(1,1) διαπιστώνουμε ότι c=0. Οπότε f^2(x)=x και άρα για κάθε x χωριστά έχουμε πρόσημο (που εξαρτάται από το x) με f(x)=\pm \sqrt x. Αρχικά, μόνο στο x=1 έχουμε την σιγουριά του +.
Για να μπορέσουμε να πούμε ότι παίρνουμε μόνο το + (παντού) χρειάζεται ένα επιχείρημα συνέχειας. Σίγουρα η αξία του ως μέρους μιας επιστημονικά τεκμηριωμένης απάντησης αξίζει περισσότερο από τις 6 μονάδες που δίνει ο θεματοθέτης. Ξέφυγε άραγε αυτό το σημείο από τον εξεταστή; Πήρε το + σε όλα τα σημεία εργαζόμενος διαισθητικά;
Θα ήθελα να έβλεπα μία απόδειξη εντός των 6 μονάδων.
Ομολογώ ότι δεν ξέρω/δεν θυμάμαι αν υπάρχει έτοιμη αιτιολόγηση αυτού του σημείου στο βιβλίο, οπότε είμαστε εντάξει. Αλλιώς ...
Με κάποιο μαγικό τρόπο διδάσκουμε πως καταλήγουμε στην σχέση f^2(x)=x
Χρειάζεται ένα εύκολο επιχείρημα ότι η f δεν έχει ρίζες (εσωτερικά) επομένως -λόγω της συνέχειας που δίνεται- διατηρεί σταθερό πρόσημο.
Στο σχολικό βιβλίο υπάρχει όμοια άσκηση στην παράγραφο της συνέχειας (άσκηση 7 Β' ομάδας)
Μήπως εννοείτε την μελέτη στο R και δεν κατάλαβα εγώ σωστά;
Re: Θέματα επαναληπτικών στα Μαθηματικά
Θα συμφωνήσω. Τους ξέφυγε να γράψουν ότι η  είναι παραγωγίσιμη στο θέμα Γ στο
είναι παραγωγίσιμη στο θέμα Γ στο  .
.
 είναι παραγωγίσιμη στο θέμα Γ στο
είναι παραγωγίσιμη στο θέμα Γ στο  .
.Είναι αυταπάτη ότι η νεότητα είναι ευτυχισμένη, μια αυταπάτη αυτών που την έχουν χάσει. W. Somerset Maugham
-
Apo.Antonis
- Δημοσιεύσεις: 21
- Εγγραφή: Δευ Απρ 02, 2018 9:52 am
Re: Θέματα επαναληπτικών στα Μαθηματικά
Υπάρχουν εφαρμογές και ασκήσεις στο βιβλίο σε αυτή τη μορφή.
-
Νίκος Ζαφειρόπουλος
- Δημοσιεύσεις: 303
- Εγγραφή: Κυρ Απρ 12, 2009 1:06 am
- Τοποθεσία: ΖΑΚΥΝΘΟΣ
- Επικοινωνία:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Θέματα επαναληπτικών στα Μαθηματικά
Δεν είπα ότι υπάρχει θέμα με το μαθηματικό μέρος του Γ1. Το μόνο που είπα είναι ότι οι 6 μονάδες που του δίνουν οι θεματοθέτες είναι λίγες γιατί χρειάζεται επιχείρημα συνέχειας για να καταλήξουμε στο +. Ιδού:
Και η λύση που δίνεις είναι ακριβώς αυτό το επιχείρημα συνέχειας που έχω και εγώ κατά νου. Σίγουρα είναι μεγάλο μέρος της απάντησης, οπότε με πόσο άραγε αξιολογούν οι θεματοθέτες το υπόλοιπο μέρος της λύσης του Γ1, αν σε αυτό το μέρος δώσουν, ας πούμε, 4-5 μόρια; Ή μήπως αξίζει λιγότερα; Αυτό λέω και τίποτα παραπάνω.Mihalis_Lambrou έγραψε: ↑Τετ Σεπ 04, 2019 9:10 pmΓια να μπορέσουμε να πούμε ότι παίρνουμε μόνο το + (παντού) χρειάζεται ένα επιχείρημα συνέχειας. Σίγουρα η αξία του ως μέρους μιας επιστημονικά τεκμηριωμένης απάντησης αξίζει περισσότερο από τις 6 μονάδες που δίνει ο θεματοθέτης. Ξέφυγε άραγε αυτό το σημείο από τον εξεταστή; Πήρε το + σε όλα τα σημεία εργαζόμενος διαισθητικά;
τελευταία επεξεργασία από Mihalis_Lambrou σε Πέμ Σεπ 05, 2019 12:34 am, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Θέματα επαναληπτικών στα Μαθηματικά
Καλησπέρα και από εμένα στην όμορφη κοινότητα του mathematica! Βλέποντας τον Κώστα να κάνει την αρχή και σαν παιδί κι εγώ που τελείωσε φέτος μπήκα στον πειρασμό να γράψω για πρώτη φορά στο forum ασχολούμενος με το θέμα Γ. Επισυνάπτω σε μορφή εικόνας τη λύση μου, διότι μόλις άρχισα να μαθαίνω latex και θα πάρει πολλή ώρα η αντιγραφή.
Φιλικά,
Γιάννης
Φιλικά,
Γιάννης
τελευταία επεξεργασία από Demetres σε Πέμ Σεπ 05, 2019 8:45 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: Διαγραφή συνδέσμων εικόνας
Λόγος: Διαγραφή συνδέσμων εικόνας
Νάκος Ιωάννης, ΗΜΜΥ ΑΠΘ
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Θέματα επαναληπτικών στα Μαθηματικά
Δεν μίλησα για αόριστο ολοκλήρωμα. Με ορισμένο ολοκλήρωμα προχωράμε. Ας το κάνω λιανά:Apo.Antonis έγραψε: ↑Τετ Σεπ 04, 2019 10:26 pm
Δεν μπορούμε να ολοκληρώσουμε καθώς το αόριστο ολοκλήρωμα είναι εκτός ύλης.
Ολοκληρώνουμε από 0 ως X την f(x)f'(x)= 1/2. Δίνει (f^2(X) - f^2(0)) = (Χ-0)/2. Διώχνουμε το 1/2 οπότε γίνεται f^2(X)= X + f^2(0), που είναι αυτή που έγραψα αλλά έβαλα x αντί X και η σταθερά f^2(0) συμβολίστηκε ως c.
-
Apo.Antonis
- Δημοσιεύσεις: 21
- Εγγραφή: Δευ Απρ 02, 2018 9:52 am
Re: Θέματα επαναληπτικών στα Μαθηματικά
κ.Λάμπρου, δεν ήταν μομφή προς εσάς ότι δεν χρησιμοποιούμε το αόριστο ολοκλήρωμα
-ούτε και την συνάρτηση ολοκλήρωμα που επίσης είναι εκτός (* εκτός της τυπολατρικής αναπαραγωγής της απόδειξης) -
το "μαγικό" που διδάσκουμε μέμφομαι.
-ούτε και την συνάρτηση ολοκλήρωμα που επίσης είναι εκτός (* εκτός της τυπολατρικής αναπαραγωγής της απόδειξης) -
το "μαγικό" που διδάσκουμε μέμφομαι.
τελευταία επεξεργασία από Apo.Antonis σε Πέμ Σεπ 05, 2019 1:09 am, έχει επεξεργασθεί 1 φορά συνολικά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Θέματα επαναληπτικών στα Μαθηματικά
Apo.Antonis έγραψε: ↑Πέμ Σεπ 05, 2019 1:06 amκ.Λάμπρου, δεν ήταν μομφή προς εσάς ότι δεν χρησιμοποιούμε το αόριστο ολοκλήρωμα
-ούτε και την συνάρτηση ολοκλήρωμα που επίσης είναι εκτός-
το "μαγικό" που διδάσκουμε μέμφομαι.
Αντώνη, έχεις δίκιο. Να ΄σαι καλά.
Re: Θέματα επαναληπτικών στα Μαθηματικά
Κύριε Μιχάλη καλημέρα. Τι λέτε για αυτή την βαθμολογία - λύση;Mihalis_Lambrou έγραψε: ↑Τετ Σεπ 04, 2019 9:10 pm(Δεν γράφω σε latex γιατί προφανώς ο ιστότοπός μας έχει σήμερα κάποιο τεχνικό πρόβλημα και δεν το δέχεται. Το παρατήρησα και το πρωί. Ας το κοιτάξουν οι φίλοι μας Διαχειριστές. Θα επαναφέρω το latex μετά την διόρθωση του προβλήματος.)
Στην Άσκηση Γ1 βλέπω κάποιο θεματάκι. Μάλλον τους ξέφυγε κάτι. Θέλω να πω:
Ολοκληρώνοντας την δοθείσα βρίσκουμε f^2(x)= x+c , που με χρήση του σημείου Μ(1,1) διαπιστώνουμε ότι c=0. Οπότε f^2(x)=x και άρα για κάθε x χωριστά έχουμε πρόσημο (που εξαρτάται από το x) με f(x)=\pm \sqrt x. Αρχικά, μόνο στο x=1 έχουμε την σιγουριά του +.
Για να μπορέσουμε να πούμε ότι παίρνουμε μόνο το + (παντού) χρειάζεται ένα επιχείρημα συνέχειας. Σίγουρα η αξία του ως μέρους μιας επιστημονικά τεκμηριωμένης απάντησης αξίζει περισσότερο από τις 6 μονάδες που δίνει ο θεματοθέτης. Ξέφυγε άραγε αυτό το σημείο από τον εξεταστή; Πήρε το + σε όλα τα σημεία εργαζόμενος διαισθητικά;
Θα ήθελα να έβλεπα μία απόδειξη εντός των 6 μονάδων.
Ομολογώ ότι δεν ξέρω/δεν θυμάμαι αν υπάρχει έτοιμη αιτιολόγηση αυτού του σημείου στο βιβλίο, οπότε είμαστε εντάξει. Αλλιώς ...
Είναι
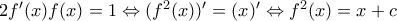 και αφού
και αφού  έχουμε
έχουμε  άρα
άρα 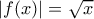 (Μονάδες3)
(Μονάδες3)Η συνάρτηση f μηδενίζεται μόνο στο μηδέν αφού
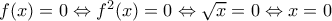 (Μονάδες 2) και είναι συνεχής άρα διατηρεί σταθερό πρόσημο στο
(Μονάδες 2) και είναι συνεχής άρα διατηρεί σταθερό πρόσημο στο  και επειδή
και επειδή  είναι
είναι  για κάθε
για κάθε  . (Μονάδες 1)
. (Μονάδες 1)Άρα
 για κάθε
για κάθε 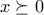
Κανάβης Χρήστος
Μαθηματικός
Μαθηματικός
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1292
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: Θέματα επαναληπτικών στα Μαθηματικά
Επειδή το Θέμα Δ είναι αξιόλογο , ας υπάρχει μια λύση στο mathematica...
Για λόγους πληρότητας της δημοσίευσης θα γράψω την διατύπωση.
ΘΕΜΑ Δ
Δίνεται η συνάρτηση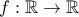 , με τύπο
, με τύπο 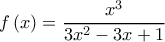 .
.
Δ1.Να αποδείξετε ότι η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 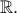
ΜΟΝΑΔΕΣ 4
Δ2.Να αποδείξετε ότι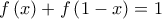 για κάθε
για κάθε  (μονάδες 2) και στη συνέχεια να αποδείξετε ότι το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση της
(μονάδες 2) και στη συνέχεια να αποδείξετε ότι το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση της  , τον άξονα
, τον άξονα  και την ευθεία
και την ευθεία  ισούται με
ισούται με 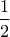 (μονάδες 4).
(μονάδες 4).
ΜΟΝΑΔΕΣ 6
Δ3.Να αποδείξετε ότι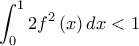
ΜΟΝΑΔΕΣ 6
Δ4.Nα λύσετε στο διάστημα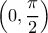 την εξίσωση
την εξίσωση
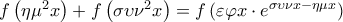
ΜΟΝΑΔΕΣ 9
Aς δούμε και την διαπραγμάτευση του θέματος...
Δ1.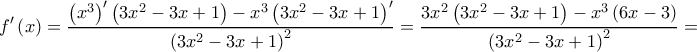
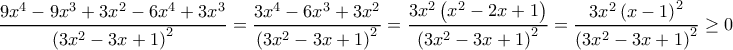
για κάθε που ανήκει στους πραγματικούς αριθμούς.
που ανήκει στους πραγματικούς αριθμούς.
Η μηδενίζεται στις θέσεις
μηδενίζεται στις θέσεις  και
και 
Συνεπώς η η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 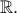
Δ2.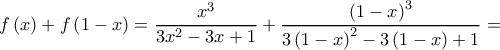
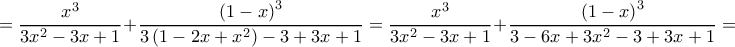
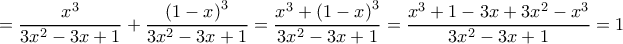
Θα αποδειχθεί ότι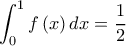
Θέτω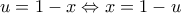 και έτσι
και έτσι 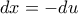
Συνεπώς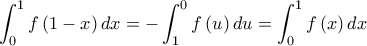
Iσχύει ότι![\displaystyle \int_{0}^{1}\left [ f\left ( x \right )+f\left ( 1-x \right ) \right ]dx=\int_{0}^{1}1dx \displaystyle \int_{0}^{1}\left [ f\left ( x \right )+f\left ( 1-x \right ) \right ]dx=\int_{0}^{1}1dx](/forum/ext/geomar/texintegr/latexrender/pictures/5a89f2cb461387435d2697a4fc6f866f.png) κάτι που συνεπάγεται ότι
κάτι που συνεπάγεται ότι
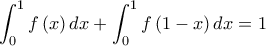 και αυτό με την σειρά του
και αυτό με την σειρά του
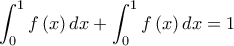 και έτσι
και έτσι 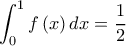
Η γραφική παράσταση της διέρχεται από την αρχή των αξόνων (αφού
διέρχεται από την αρχή των αξόνων (αφού  ) και
) και 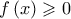 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
Άρα το ζητούμενο εμβαδόν είναι ίσο με το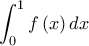 που όπως είδαμε είναι ίσο με
που όπως είδαμε είναι ίσο με 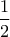
Δ3. Έχουμε ήδη δει ότι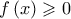 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
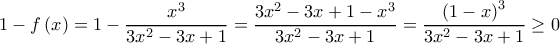 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
Έτσι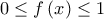 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
Συνεπώς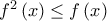 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
H συνάρτηση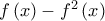 δεν είναι παντού μηδέν στο
δεν είναι παντού μηδέν στο ![\left [ 0,1 \right ] \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/16cd21d3a9a2009a63669f9d468c132f.png) μολονότι είναι μη αρνητική στο διάστημα αυτό.
μολονότι είναι μη αρνητική στο διάστημα αυτό.
Άρα μπορεί να γραφεί ότι![\displaystyle\int_{0}^{1}\left [ f\left ( x \right )-f^{2}\left ( x \right ) \right ]dx> 0 \displaystyle\int_{0}^{1}\left [ f\left ( x \right )-f^{2}\left ( x \right ) \right ]dx> 0](/forum/ext/geomar/texintegr/latexrender/pictures/4b93a969e6e0ef95f8cbbcbbe707a987.png) και αυτό σημαίνει
και αυτό σημαίνει 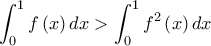
Άρα λοιπόν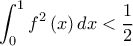
δηλαδή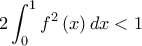 και έτσι
και έτσι 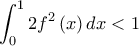
Δ4. Από την ταυτότητα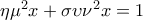 και από το πρώτο κομμάτι του Δ2 η εξίσωση γράφεται ισοδύναμα
και από το πρώτο κομμάτι του Δ2 η εξίσωση γράφεται ισοδύναμα
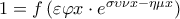
Η τελευταία ισοδυναμεί με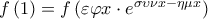
Είδαμε στο Δ1 ότι η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 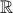 άρα και 1-1 σε αυτό.
άρα και 1-1 σε αυτό.
Συνεπώς ισοδύναμα έχουμε ότι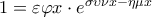
Σίγουρα ο αριθμός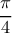 είναι λύση της εξίσωσης . Θα αποδείξουμε ότι είναι και μοναδική.
είναι λύση της εξίσωσης . Θα αποδείξουμε ότι είναι και μοναδική.
Έστω η συνάρτηση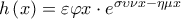 ,
, 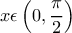
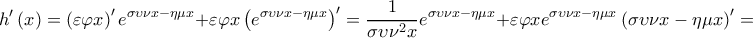
![\displaystyle e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\varepsilon \varphi x\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]=e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\frac{\eta \mu x}{\sigma \upsilon \nu x}\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]= \displaystyle e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\varepsilon \varphi x\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]=e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\frac{\eta \mu x}{\sigma \upsilon \nu x}\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/744ab57a559af140e66d172e83dc5bc9.png)
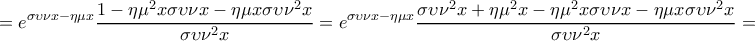
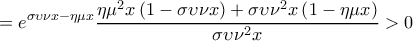 για κάθε
για κάθε 
Άρα η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 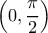
Άρα ο αριθμός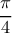 είναι η μοναδική λύση της εξίσωσης που μας έδωσαν.
είναι η μοναδική λύση της εξίσωσης που μας έδωσαν.
Κάτι δεν έγραψα καΛά , έγινε κάποιο λάθος το οποίο και διόρθωσα...
Ευχαριστώ τον Χρήστο και τον Θανάση για την επισήμανση.
Για λόγους πληρότητας της δημοσίευσης θα γράψω την διατύπωση.
ΘΕΜΑ Δ
Δίνεται η συνάρτηση
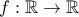 , με τύπο
, με τύπο 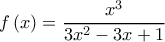 .
.Δ1.Να αποδείξετε ότι η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 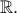
ΜΟΝΑΔΕΣ 4
Δ2.Να αποδείξετε ότι
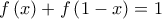 για κάθε
για κάθε  (μονάδες 2) και στη συνέχεια να αποδείξετε ότι το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση της
(μονάδες 2) και στη συνέχεια να αποδείξετε ότι το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση της  , τον άξονα
, τον άξονα  και την ευθεία
και την ευθεία  ισούται με
ισούται με 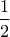 (μονάδες 4).
(μονάδες 4).ΜΟΝΑΔΕΣ 6
Δ3.Να αποδείξετε ότι
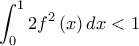
ΜΟΝΑΔΕΣ 6
Δ4.Nα λύσετε στο διάστημα
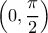 την εξίσωση
την εξίσωση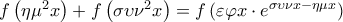
ΜΟΝΑΔΕΣ 9
Aς δούμε και την διαπραγμάτευση του θέματος...
Δ1.
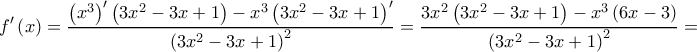
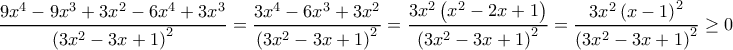
για κάθε
 που ανήκει στους πραγματικούς αριθμούς.
που ανήκει στους πραγματικούς αριθμούς.Η
 μηδενίζεται στις θέσεις
μηδενίζεται στις θέσεις  και
και 
Συνεπώς η η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 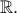
Δ2.
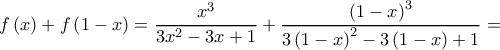
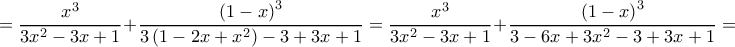
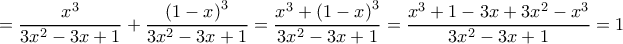
Θα αποδειχθεί ότι
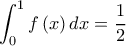
Θέτω
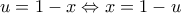 και έτσι
και έτσι 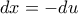
Συνεπώς
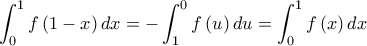
Iσχύει ότι
![\displaystyle \int_{0}^{1}\left [ f\left ( x \right )+f\left ( 1-x \right ) \right ]dx=\int_{0}^{1}1dx \displaystyle \int_{0}^{1}\left [ f\left ( x \right )+f\left ( 1-x \right ) \right ]dx=\int_{0}^{1}1dx](/forum/ext/geomar/texintegr/latexrender/pictures/5a89f2cb461387435d2697a4fc6f866f.png) κάτι που συνεπάγεται ότι
κάτι που συνεπάγεται ότι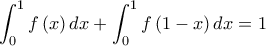 και αυτό με την σειρά του
και αυτό με την σειρά του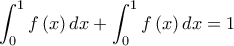 και έτσι
και έτσι 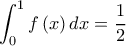
Η γραφική παράσταση της
 διέρχεται από την αρχή των αξόνων (αφού
διέρχεται από την αρχή των αξόνων (αφού  ) και
) και 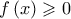 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
Άρα το ζητούμενο εμβαδόν είναι ίσο με το
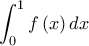 που όπως είδαμε είναι ίσο με
που όπως είδαμε είναι ίσο με 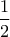
Δ3. Έχουμε ήδη δει ότι
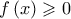 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
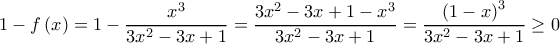 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
Έτσι
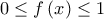 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
Συνεπώς
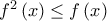 για κάθε
για κάθε ![x\epsilon \left [ 0,1 \right ] x\epsilon \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/63eb1662892377338c63d4d7539dd223.png)
H συνάρτηση
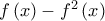 δεν είναι παντού μηδέν στο
δεν είναι παντού μηδέν στο ![\left [ 0,1 \right ] \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/16cd21d3a9a2009a63669f9d468c132f.png) μολονότι είναι μη αρνητική στο διάστημα αυτό.
μολονότι είναι μη αρνητική στο διάστημα αυτό.Άρα μπορεί να γραφεί ότι
![\displaystyle\int_{0}^{1}\left [ f\left ( x \right )-f^{2}\left ( x \right ) \right ]dx> 0 \displaystyle\int_{0}^{1}\left [ f\left ( x \right )-f^{2}\left ( x \right ) \right ]dx> 0](/forum/ext/geomar/texintegr/latexrender/pictures/4b93a969e6e0ef95f8cbbcbbe707a987.png) και αυτό σημαίνει
και αυτό σημαίνει 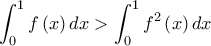
Άρα λοιπόν
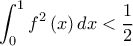
δηλαδή
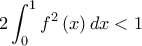 και έτσι
και έτσι 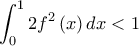
Δ4. Από την ταυτότητα
 και από το πρώτο κομμάτι του Δ2 η εξίσωση γράφεται ισοδύναμα
και από το πρώτο κομμάτι του Δ2 η εξίσωση γράφεται ισοδύναμα 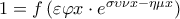
Η τελευταία ισοδυναμεί με
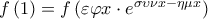
Είδαμε στο Δ1 ότι η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 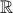 άρα και 1-1 σε αυτό.
άρα και 1-1 σε αυτό.Συνεπώς ισοδύναμα έχουμε ότι
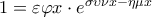
Σίγουρα ο αριθμός
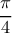 είναι λύση της εξίσωσης . Θα αποδείξουμε ότι είναι και μοναδική.
είναι λύση της εξίσωσης . Θα αποδείξουμε ότι είναι και μοναδική.Έστω η συνάρτηση
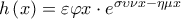 ,
, 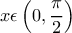
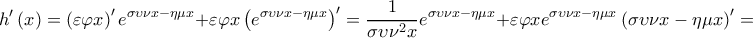
![\displaystyle e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\varepsilon \varphi x\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]=e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\frac{\eta \mu x}{\sigma \upsilon \nu x}\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]= \displaystyle e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\varepsilon \varphi x\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]=e^{\sigma \upsilon \nu x-\eta \mu x}\left [ \frac{1}{\sigma \upsilon \nu ^{2}x} +\frac{\eta \mu x}{\sigma \upsilon \nu x}\left ( -\eta \mu x-\sigma \upsilon \nu x \right )\right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/744ab57a559af140e66d172e83dc5bc9.png)
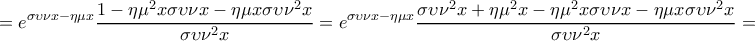
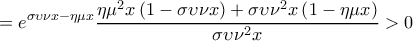 για κάθε
για κάθε 
Άρα η
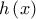 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 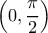
Άρα ο αριθμός
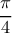 είναι η μοναδική λύση της εξίσωσης που μας έδωσαν.
είναι η μοναδική λύση της εξίσωσης που μας έδωσαν.Κάτι δεν έγραψα καΛά , έγινε κάποιο λάθος το οποίο και διόρθωσα...
Ευχαριστώ τον Χρήστο και τον Θανάση για την επισήμανση.
τελευταία επεξεργασία από ΚΕΦΑΛΟΝΙΤΗΣ σε Σάβ Μαρ 28, 2020 10:06 pm, έχει επεξεργασθεί 3 φορές συνολικά.
- Christos.N
- Δημοσιεύσεις: 2105
- Εγγραφή: Πέμ Νοέμ 26, 2009 2:28 pm
- Τοποθεσία: Ίλιον
Re: Θέματα επαναληπτικών στα Μαθηματικά
Δ4. Από την ταυτότητα
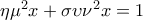 και από το πρώτο κομμάτι του Δ2 η εξίσωση γράφεται ισοδύναμα
και από το πρώτο κομμάτι του Δ2 η εξίσωση γράφεται ισοδύναμα 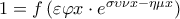
Η τελευταία ισοδυναμεί με
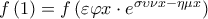
Είδαμε στο Δ1 ότι η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 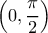
 άρα και 1-1 σε αυτό.
άρα και 1-1 σε αυτό.Συνεπώς ισοδύναμα έχουμε ότι
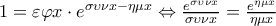
Έστω η συνάρτηση
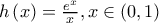
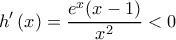
Άρα η
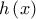 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 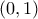 άρα και
άρα και  .
.για
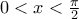 θα είναι
θα είναι 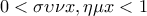
άρα

Υ.Γ.:
 Όπως μου επισήμανε ο Θανάσης (socrates) το πεδίο ορισμού του ορίσματος της συνάρτηση
Όπως μου επισήμανε ο Θανάσης (socrates) το πεδίο ορισμού του ορίσματος της συνάρτηση  στο δεύτερο μέλος της ισότητας είναι το σύνολο
στο δεύτερο μέλος της ισότητας είναι το σύνολο  και όχι το φτωχό
και όχι το φτωχό  άρα είναι μεν "1-1" αλλά στο
άρα είναι μεν "1-1" αλλά στο 
τελευταία επεξεργασία από Christos.N σε Παρ Μαρ 27, 2020 8:53 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Χρήστος Ντάβας
Wir müssen wissen — wir werden wissen! D.Hilbert
Wir müssen wissen — wir werden wissen! D.Hilbert
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες