- them_mathimatika_epan_230909-1.pdf
- (227.24 KiB) Μεταφορτώθηκε 142 φορές
Θέματα επαναληπτικών 2023
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1292
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: Θέματα επαναληπτικών 2023
Το 2023 είχαμε δύο επαναληπτικές εξετάσεις στα Μαθηματικά.
Οι πρώτες έγιναν στις 9 Σεπτεμβρίου. Λόγω των έκτακτων συνθηκών που έπληξαν κάποιες περιοχές της Ελλάδας εκείνες τις στιγμές
αποφασίστηκε να γίνουν στις 15 Σεπτεμβρίου επαναληπτικές εξετάσεις σε Αρχαία, Μαθηματικά και Βιολογία.
Αυτό γιατί κάποιοι υποψήφιοι είχαν αδυναμία προσέλευσης στα εξεταστικά κέντρα στις 9 Σεπτεμβρίου.
Παρακάτω επισυνάπτω τα θέματα των δεύτερων επαναληπτικών εξετάσεων στα Μαθηματικά.
Οι πρώτες έγιναν στις 9 Σεπτεμβρίου. Λόγω των έκτακτων συνθηκών που έπληξαν κάποιες περιοχές της Ελλάδας εκείνες τις στιγμές
αποφασίστηκε να γίνουν στις 15 Σεπτεμβρίου επαναληπτικές εξετάσεις σε Αρχαία, Μαθηματικά και Βιολογία.
Αυτό γιατί κάποιοι υποψήφιοι είχαν αδυναμία προσέλευσης στα εξεταστικά κέντρα στις 9 Σεπτεμβρίου.
Παρακάτω επισυνάπτω τα θέματα των δεύτερων επαναληπτικών εξετάσεων στα Μαθηματικά.
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1292
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: Θέματα επαναληπτικών 2023
Aς δούμε το 4ο θέμα της 15-9-2023.
ΘΕΜΑ Δ
Δίνεται η συνεχής συνάρτηση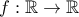 για την οποία ισχύει:
για την οποία ισχύει:
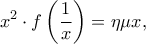 για κάθε
για κάθε 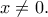
Δ1. Να αποδείξετε ότι![f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases} f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/8272c88ccc19b8867954f9b460441f9c.png)
ΜΟΝΑΔΕΣ 5
Δ2. Να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της συνάρτησης στο σημείο
στο σημείο 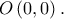
ΜΟΝΑΔΕΣ 8
Δ3. Nα βρείτε την ασύμπτωτη της γραφικής παράστασης της στο
στο 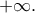
ΜΟΝΑΔΕΣ 6
Δ4. Να υπολογίσετε το ολοκλήρωμα
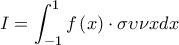
ΜΟΝΑΔΕΣ 6
ΛΥΣΗ
Δ1. Ας δούμε τι γίνεται όταν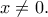
Aν στη θέση του μπει το
μπει το  προκύπτει ότι
προκύπτει ότι
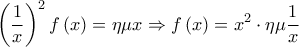
H είναι συνεχής σε όλο το
είναι συνεχής σε όλο το 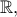 άρα και στο
άρα και στο 
Άρα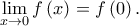
Όμως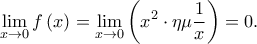
Aν κάποιος δεν καταλαβαίνει γιατί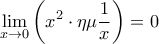 , αυτό προκύπτει
, αυτό προκύπτει
από το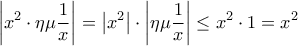
που ισοδυναμεί με την ανισότητα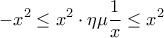 και με χρήση του κριτηρίου παρεμβολής.
και με χρήση του κριτηρίου παρεμβολής.
Συνεπώς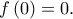
Aποδείχθηκε λοιπόν ότι![f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases} f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/8272c88ccc19b8867954f9b460441f9c.png)
Δ2. Κατ' αρχήν ισχύει ότι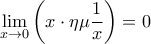 .
.
Η απόδειξη είναι εντελώς ίδια με την απόδειξη του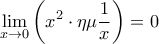 .
.
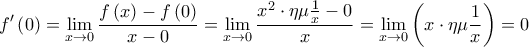
H εφαπτομένη της γραφικής παράστασης της στο σημείο
στο σημείο 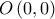 έχει εξίσωση
έχει εξίσωση
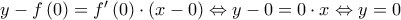
H ζητούμενη εφαπτομένη είναι ο άξονας των τετμημένων.
Δ3.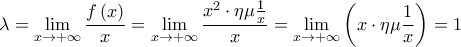
![\displaystyle\beta =\lim_{x \rightarrow +\infty}\left [ f\left ( x \right )-x \right ]=\lim_{x \rightarrow +\infty}\left ( x^{2}\cdot \eta \mu \frac{1}{x}-x \right )=\lim_{x \rightarrow +\infty}\left [ x \left ( x\cdot \eta \mu \frac{1}{x}-1 \right ) \right ]= \displaystyle\beta =\lim_{x \rightarrow +\infty}\left [ f\left ( x \right )-x \right ]=\lim_{x \rightarrow +\infty}\left ( x^{2}\cdot \eta \mu \frac{1}{x}-x \right )=\lim_{x \rightarrow +\infty}\left [ x \left ( x\cdot \eta \mu \frac{1}{x}-1 \right ) \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/97241195ec6814dc9a3e9456af8dfdd3.png)
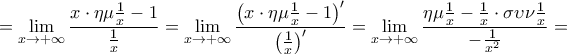
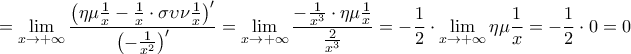
Άρα η ευθεία με εξίσωση είναι πλάγια ασύμπτωτη της γραφικής παράστασης της
είναι πλάγια ασύμπτωτη της γραφικής παράστασης της  στο
στο 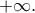
Νομίζω ότι εύκολα καταλαβαίνει κάποιος ότι η ίδια ευθεία είναι πλάγια ασύμπτωτη της γραφικής παράστασης της στο
στο 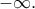
Δ4. Δε σκοπεύω να κουράσω γράφοντας πολλά για αυτό το σκέλος...
Η συνάρτηση![g\left ( x \right )=f\left ( x \right )\cdot \sigma \upsilon \nu x, x\epsilon \left [ -1,1 \right ] g\left ( x \right )=f\left ( x \right )\cdot \sigma \upsilon \nu x, x\epsilon \left [ -1,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b595222f5b20e684824abf3d827a801d.png) μπορεί εύκολα να
μπορεί εύκολα να
διαπιστωθεί ότι είναι περιττή. Άρα το ζητούμενο ολοκλήρωμα είναι ίσο με
Συναρτήσεις όπως η του θέματος αυτού με συνάρπαζαν όταν ήμουν υποψήφιος της 1ης Δέσμης.
του θέματος αυτού με συνάρπαζαν όταν ήμουν υποψήφιος της 1ης Δέσμης.
ΘΕΜΑ Δ
Δίνεται η συνεχής συνάρτηση
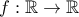 για την οποία ισχύει:
για την οποία ισχύει: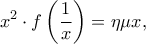 για κάθε
για κάθε 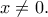
Δ1. Να αποδείξετε ότι
![f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases} f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/8272c88ccc19b8867954f9b460441f9c.png)
ΜΟΝΑΔΕΣ 5
Δ2. Να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της συνάρτησης
 στο σημείο
στο σημείο 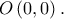
ΜΟΝΑΔΕΣ 8
Δ3. Nα βρείτε την ασύμπτωτη της γραφικής παράστασης της
 στο
στο 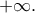
ΜΟΝΑΔΕΣ 6
Δ4. Να υπολογίσετε το ολοκλήρωμα
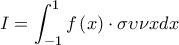
ΜΟΝΑΔΕΣ 6
ΛΥΣΗ
Δ1. Ας δούμε τι γίνεται όταν
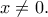
Aν στη θέση του
 μπει το
μπει το  προκύπτει ότι
προκύπτει ότι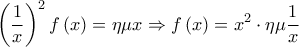
H
 είναι συνεχής σε όλο το
είναι συνεχής σε όλο το 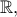 άρα και στο
άρα και στο 
Άρα
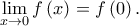
Όμως
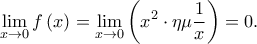
Aν κάποιος δεν καταλαβαίνει γιατί
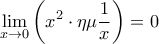 , αυτό προκύπτει
, αυτό προκύπτει από το
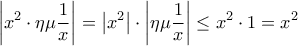
που ισοδυναμεί με την ανισότητα
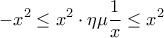 και με χρήση του κριτηρίου παρεμβολής.
και με χρήση του κριτηρίου παρεμβολής.Συνεπώς
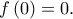
Aποδείχθηκε λοιπόν ότι
![f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases} f\left ( x \right ) =\begin{cases}\displaystyle x^{2} \cdot \eta \mu \frac{1}{x}, x\neq 0 \right ] \\ 0, \displaystyle,x=0\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/8272c88ccc19b8867954f9b460441f9c.png)
Δ2. Κατ' αρχήν ισχύει ότι
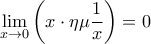 .
.Η απόδειξη είναι εντελώς ίδια με την απόδειξη του
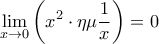 .
.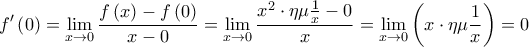
H εφαπτομένη της γραφικής παράστασης της
 στο σημείο
στο σημείο 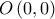 έχει εξίσωση
έχει εξίσωση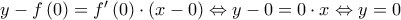
H ζητούμενη εφαπτομένη είναι ο άξονας των τετμημένων.
Δ3.
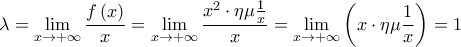
![\displaystyle\beta =\lim_{x \rightarrow +\infty}\left [ f\left ( x \right )-x \right ]=\lim_{x \rightarrow +\infty}\left ( x^{2}\cdot \eta \mu \frac{1}{x}-x \right )=\lim_{x \rightarrow +\infty}\left [ x \left ( x\cdot \eta \mu \frac{1}{x}-1 \right ) \right ]= \displaystyle\beta =\lim_{x \rightarrow +\infty}\left [ f\left ( x \right )-x \right ]=\lim_{x \rightarrow +\infty}\left ( x^{2}\cdot \eta \mu \frac{1}{x}-x \right )=\lim_{x \rightarrow +\infty}\left [ x \left ( x\cdot \eta \mu \frac{1}{x}-1 \right ) \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/97241195ec6814dc9a3e9456af8dfdd3.png)
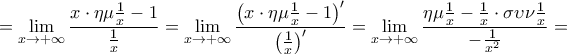
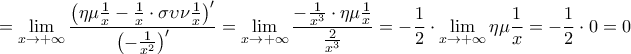
Άρα η ευθεία με εξίσωση
 είναι πλάγια ασύμπτωτη της γραφικής παράστασης της
είναι πλάγια ασύμπτωτη της γραφικής παράστασης της  στο
στο 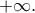
Νομίζω ότι εύκολα καταλαβαίνει κάποιος ότι η ίδια ευθεία είναι πλάγια ασύμπτωτη της γραφικής παράστασης της
 στο
στο 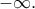
Δ4. Δε σκοπεύω να κουράσω γράφοντας πολλά για αυτό το σκέλος...
Η συνάρτηση
![g\left ( x \right )=f\left ( x \right )\cdot \sigma \upsilon \nu x, x\epsilon \left [ -1,1 \right ] g\left ( x \right )=f\left ( x \right )\cdot \sigma \upsilon \nu x, x\epsilon \left [ -1,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b595222f5b20e684824abf3d827a801d.png) μπορεί εύκολα να
μπορεί εύκολα να διαπιστωθεί ότι είναι περιττή. Άρα το ζητούμενο ολοκλήρωμα είναι ίσο με

Συναρτήσεις όπως η
 του θέματος αυτού με συνάρπαζαν όταν ήμουν υποψήφιος της 1ης Δέσμης.
του θέματος αυτού με συνάρπαζαν όταν ήμουν υποψήφιος της 1ης Δέσμης. Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
