 σε άθροισμα δυο κλασμάτων που να έχουν παρανομαστές
σε άθροισμα δυο κλασμάτων που να έχουν παρανομαστές  και
και 
β) Να λυθεί το σύστημα

2. α) Να λυθεί το σύστημα
![\displaystyle{\begin{cases}
x^y=243\\
\sqrt[y]{1024} =\displaystyle \left(\frac{2}{3}x\right)^2
\end{cases}} \displaystyle{\begin{cases}
x^y=243\\
\sqrt[y]{1024} =\displaystyle \left(\frac{2}{3}x\right)^2
\end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/a3fc9a37ea08c317af38dc9a3b7943db.png)
β) Να λυθεί το σύστημα
![\displaystyle{\begin{cases}
xy=100 \\
\displaystyle\frac{x}{y}=2 \sqrt[3]{\displaystyle x^\log x}
\end{cases}} \displaystyle{\begin{cases}
xy=100 \\
\displaystyle\frac{x}{y}=2 \sqrt[3]{\displaystyle x^\log x}
\end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/ba58738daa82b25a80840cda6d902c85.png)
3. Οι αριθμοί
 αποτελούν γεωμετρική πρόοδο.
αποτελούν γεωμετρική πρόοδο.Το άθροισμα των δυο άκρων είναι ίσο με
 και των δύο μέσων είναι ίσο με
και των δύο μέσων είναι ίσο με  .
.Να βρεθούν οι
 .
.4. Σε φθίνουσα γεωμετρική πρόοδο οι τρεις πρώτοι όροι έχουν άθροισμα 21, οι τρεις επόμενοι όροι
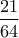 .
.Να βρείτε το άθροισμα των άπειρων όρων της γεωμετρικής προόδου.
edit
μετονομασία από ΕΜΠ 1931 ΠΟΛ.ΜΗΧ. ΑΛΓΕΒΡΑ σε ΕΜΠ 1931 ΑΛΓΕΒΡΑ ΠΟΛ.ΜΗΧ. γιατί μερικά τμήματα είχαν τα ίδια θέματα

 ακέραιοι αριθμοί τέτοιοι ώστε
ακέραιοι αριθμοί τέτοιοι ώστε 
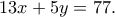

 με
με  ακέραιο.
ακέραιο.

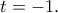
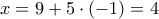 και
και 
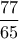 ως άθροισμα δυο κλασμάτων είναι
ως άθροισμα δυο κλασμάτων είναι 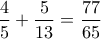
 και
και 
![\sqrt[y]{1024} =\displaystyle \left(\frac{2}{3}x\right)^2 \sqrt[y]{1024} =\displaystyle \left(\frac{2}{3}x\right)^2](/forum/ext/geomar/texintegr/latexrender/pictures/1e96de93b41d6b596bf04ca46d5d543a.png)

![\sqrt[y]{2^{10}} =\displaystyle \left(\frac{2}{3}x\right)^2 \sqrt[y]{2^{10}} =\displaystyle \left(\frac{2}{3}x\right)^2](/forum/ext/geomar/texintegr/latexrender/pictures/eae0f4a8cc2410552c91e1fe51ac77d7.png)





 , από όπου προκύπτει
, από όπου προκύπτει 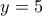



![\displaystyle\frac{x}{y}=2 \sqrt[3]{\displaystyle x^\log x} \displaystyle\frac{x}{y}=2 \sqrt[3]{\displaystyle x^\log x}](/forum/ext/geomar/texintegr/latexrender/pictures/e00324b1213fee1e41dad412a786f530.png)
![log x -log y = log 2 + log \sqrt[3]{\displaystyle x^\log x} log x -log y = log 2 + log \sqrt[3]{\displaystyle x^\log x}](/forum/ext/geomar/texintegr/latexrender/pictures/e6d2f0b5b18242c34f27e287c1fed3d8.png)



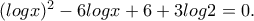
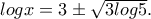
 τότε από την
τότε από την 
 και
και 
 τότε από την
τότε από την 
 και
και 
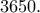
 , όπου
, όπου  ο λόγος της γεωμετρικής προόδου.
ο λόγος της γεωμετρικής προόδου.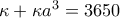






 και το
και το 
 τότε πολύ εύκολα προκύπτει ότι
τότε πολύ εύκολα προκύπτει ότι 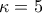 .
.
 προκύπτει ότι
προκύπτει ότι 

![\displaystyle{\begin{cases}
xy=1000 \\
\displaystyle\frac{x}{y}= \sqrt[3]{\displaystyle x^\log x}
\end{cases}} \displaystyle{\begin{cases}
xy=1000 \\
\displaystyle\frac{x}{y}= \sqrt[3]{\displaystyle x^\log x}
\end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/05efa11ae18ef800ccbb6a07752dcbd5.png)
 και όχι
και όχι 

![\displaystyle logx-logy=log\sqrt[3]{x^{logx}}\Leftrightarrow logx-logy=logx^{\frac{logx}{3}}\Leftrightarrow logx-logy=logx\cdot \frac{logx}{3} \displaystyle logx-logy=log\sqrt[3]{x^{logx}}\Leftrightarrow logx-logy=logx^{\frac{logx}{3}}\Leftrightarrow logx-logy=logx\cdot \frac{logx}{3}](/forum/ext/geomar/texintegr/latexrender/pictures/7521e864edc34516d51fa764fe0f73a9.png)



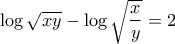

 της οποίας η διακρίνουσα είναι ίση με
της οποίας η διακρίνουσα είναι ίση με 
 ή
ή 



 που ισοδύναμα δίνει
που ισοδύναμα δίνει 

![\displaystyle\sqrt[y]{1024}=\left ( \frac{2}{3}x^{2} \right )\Leftrightarrow \left ( \sqrt[y]{2^{10}} \right )^{y}=\left [ \left ( \frac{2}{3}x \right )^{2} \right ]^{y}\Leftrightarrow 2^{10}=\left ( \frac{2}{3}x \right )^{2y}\Leftrightarrow 2^{10}=\left ( \frac{2}{3} \right )^{2y} \cdot x^{2y} \displaystyle\sqrt[y]{1024}=\left ( \frac{2}{3}x^{2} \right )\Leftrightarrow \left ( \sqrt[y]{2^{10}} \right )^{y}=\left [ \left ( \frac{2}{3}x \right )^{2} \right ]^{y}\Leftrightarrow 2^{10}=\left ( \frac{2}{3}x \right )^{2y}\Leftrightarrow 2^{10}=\left ( \frac{2}{3} \right )^{2y} \cdot x^{2y}](/forum/ext/geomar/texintegr/latexrender/pictures/5b01e0864f04a09c52723569ef070daf.png)



 , δηλαδή
, δηλαδή  , δηλαδή
, δηλαδή 