 για
για  , όπου
, όπου  πληρούν τις σχέσεις
πληρούν τις σχέσεις  . Να δείξετε οτι τότε έχουμε
. Να δείξετε οτι τότε έχουμε  .
. Μπορεί να ισχύει
 και
και  για
για  ;
;2. Έστω
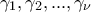 οι όροι γεωμετρική προόδου με θετικούς όρους και λόγο μεγαλύτερο ή μικρότερο της μονάδας. Να δείξετε ότι οι όροι μιας αριθμητικής προόδου
οι όροι γεωμετρική προόδου με θετικούς όρους και λόγο μεγαλύτερο ή μικρότερο της μονάδας. Να δείξετε ότι οι όροι μιας αριθμητικής προόδου  της οποίας οι δυο πρώτοι είναι ίσοι με τους αντίστοιχους όρους της γεωμετρικής προόδου, δηλαδή είναι
της οποίας οι δυο πρώτοι είναι ίσοι με τους αντίστοιχους όρους της γεωμετρικής προόδου, δηλαδή είναι 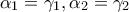 , είναι από τον τρίτο όρο και μετά μικρότεροι των αντίστοιχων όρων της γεωμετρικής προόδου, δηλαδή
, είναι από τον τρίτο όρο και μετά μικρότεροι των αντίστοιχων όρων της γεωμετρικής προόδου, δηλαδή  για
για  . Γι' αυτό να στηριχτείτε στην πρόταση, την οποία να αποδείξετε, οτι εαν σε αναλογία με θετικούς όρους κάθε όρος είναι μικρότερος των τριών άλλων, τότε το άθροισμα του μεγαλύτερου και του μικρότερου όρου είναι μεγαλύτερο του αθροίσματος των δυο άλλων.
. Γι' αυτό να στηριχτείτε στην πρόταση, την οποία να αποδείξετε, οτι εαν σε αναλογία με θετικούς όρους κάθε όρος είναι μικρότερος των τριών άλλων, τότε το άθροισμα του μεγαλύτερου και του μικρότερου όρου είναι μεγαλύτερο του αθροίσματος των δυο άλλων.3. α) Να δείξετε οτι για πραγματικούς αριθμούς
 ισχύει
ισχύει  .
.Ποιες τιμές ώστε να πληρούν τις παραπάνω σχέσεις, μπορούν να λάβουν τα
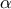 και
και  ;
;β) Να δείξετε οτι αν θέσουμε
 όπου
όπου 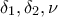 ακέραιοι αριθμοί και επιπλέον
ακέραιοι αριθμοί και επιπλέον  , ότι πρέπει να έχουμε
, ότι πρέπει να έχουμε  .
.
 .
.  και όχι
και όχι  .
. για κάθε
για κάθε  με
με 


 η τελευταία ανισότητα ισοδυναμεί με τη ζητουμένη ανισότητα
η τελευταία ανισότητα ισοδυναμεί με τη ζητουμένη ανισότητα  έχουμε
έχουμε  για κάθε
για κάθε  , αυτό όμως αντιτίθεται στο δεδομένο ότι
, αυτό όμως αντιτίθεται στο δεδομένο ότι  .
.
 .
. 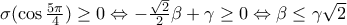 .
.  .
.