 δια του ακεραίου πολυωνύμου
δια του ακεραίου πολυωνύμου  βαθμού
βαθμού  , έστω
, έστω  το πηλίκο και
το πηλίκο και  το υπόλοιπο της διαίρεσης αυτής. Με αυτόν τον τρόπο, έχουμε την ταυτότητα
το υπόλοιπο της διαίρεσης αυτής. Με αυτόν τον τρόπο, έχουμε την ταυτότητα  όπου
όπου  ή
ή  με βαθμό
με βαθμό  μικρότερου του
μικρότερου του  . Να δείξετε οτι η παραπάνω διαίρεση γίνεται κατά μοναδικό τρόπο, οτι δηλαδή από κάθε ταυτότητα
. Να δείξετε οτι η παραπάνω διαίρεση γίνεται κατά μοναδικό τρόπο, οτι δηλαδή από κάθε ταυτότητα  με
με  ακέραια πολυώνυμα και βαθμό
ακέραια πολυώνυμα και βαθμό  , εφόσον
, εφόσον  , να συνεπάγεται ότι
, να συνεπάγεται ότι  και
και 
β) Να δείξετε οτι αν δυο (τουλάχιστον) από τις ρίζες της εξίσωσης
 είναι αντίθετες, τότε ένας τουλάχιστον, είτε από τις πραγματικούς ή τις φανταστικούς συντελεστές,
είναι αντίθετες, τότε ένας τουλάχιστον, είτε από τις πραγματικούς ή τις φανταστικούς συντελεστές, 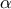 και
και  μηδενίζεται κι αντίστροφα.
μηδενίζεται κι αντίστροφα.2. Δίνονται οι εξισώσεις
 με συντελεστές πραγματικούς ή μιγαδικούς μη μηδενικούς. Η (2) έχει μόνο μια θετική ρίζα την
με συντελεστές πραγματικούς ή μιγαδικούς μη μηδενικούς. Η (2) έχει μόνο μια θετική ρίζα την  . Να δειχθεί για κάθε ρίζα της (1) , ισχύει η ανισότητα
. Να δειχθεί για κάθε ρίζα της (1) , ισχύει η ανισότητα  . Αν η (3) έχει δυο θετικές ρίζες
. Αν η (3) έχει δυο θετικές ρίζες  και
και 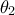 διαφορετικές μεταξύ τους, να δειχθεί οτι δεν υπάρχει ρίζα
διαφορετικές μεταξύ τους, να δειχθεί οτι δεν υπάρχει ρίζα  της (1) που να επαληθεύει την διπλή ανισότητα
της (1) που να επαληθεύει την διπλή ανισότητα  , εαν
, εαν 
3. Να δειχτεί οτι ο πραγματικός αριθμός
![\displaystyle{\sqrt[3]{2}} \displaystyle{\sqrt[3]{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/7a29452f2b506ce26979829909ad4c33.png) δεν μπορεί να είναι ρίζα της εξίσωσης
δεν μπορεί να είναι ρίζα της εξίσωσης  , εαν
, εαν  είναι ρητοί, δηλαδή από την σχέση
είναι ρητοί, δηλαδή από την σχέση ![\displaystyle{\alpha (\sqrt[3]{2})^2+\beta (\sqrt[3]{2})+\gamma=0} \displaystyle{\alpha (\sqrt[3]{2})^2+\beta (\sqrt[3]{2})+\gamma=0}](/forum/ext/geomar/texintegr/latexrender/pictures/e9f5278ef420ed0013d006ff6496b798.png) προκύπτει αναγκαστικά
προκύπτει αναγκαστικά  .
.
 .
. και με
και με ![\displaystyle{ab\sqrt[3]{4}+b^2\sqrt[3]{2}+bc=0} \displaystyle{ab\sqrt[3]{4}+b^2\sqrt[3]{2}+bc=0}](/forum/ext/geomar/texintegr/latexrender/pictures/d10447f22306a96bb1926a4970070d40.png) και
και ![\displaystyle{a\sqrt[3]{8}+b\sqrt[3]{4}+c\sqrt[3]{2}=0\overset{\cdot a}\Rightarrow 2a^2+ab\sqrt[3]{4}+ac\sqrt[3]{2}=0} \displaystyle{a\sqrt[3]{8}+b\sqrt[3]{4}+c\sqrt[3]{2}=0\overset{\cdot a}\Rightarrow 2a^2+ab\sqrt[3]{4}+ac\sqrt[3]{2}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/7893c272222e72cb22f2fee8b6ae2b1a.png) .
.![\displaystyle{b^2\sqrt[3]{2}+bc-2a^2-ac\sqrt[3]{2}=0\Rightarrow (b^2-ac)\sqrt[3]{2}+(bc-2a^2)=0} \displaystyle{b^2\sqrt[3]{2}+bc-2a^2-ac\sqrt[3]{2}=0\Rightarrow (b^2-ac)\sqrt[3]{2}+(bc-2a^2)=0}](/forum/ext/geomar/texintegr/latexrender/pictures/78f6960f49f4beb6f3a3b3c12a33059b.png)
 Αν
Αν  τότε θα είχαμε
τότε θα είχαμε ![\displaystyle{\sqrt[3]{2}=\frac{2a^2-bc}{b^2-ac}\in \mathbb Q} \displaystyle{\sqrt[3]{2}=\frac{2a^2-bc}{b^2-ac}\in \mathbb Q}](/forum/ext/geomar/texintegr/latexrender/pictures/ae05a26bca9ce3f220d8473f9ec9d807.png) (άτοπο)
(άτοπο) τότε έχουμε
τότε έχουμε  , επομένως καταλήγουμε στο σύστημα
, επομένως καταλήγουμε στο σύστημα 

 Aν
Aν  τότε από την (1) έχουμε
τότε από την (1) έχουμε  και από την αρχική
και από την αρχική 

 Aν
Aν  , θα είχαμε
, θα είχαμε ![\displaystyle{\left(\frac{c}{b}\right)^3=2\Rightarrow \frac{c}{b}=\sqrt[3]{2}\notin \mathbb Q} \displaystyle{\left(\frac{c}{b}\right)^3=2\Rightarrow \frac{c}{b}=\sqrt[3]{2}\notin \mathbb Q}](/forum/ext/geomar/texintegr/latexrender/pictures/0516c0fc2d45f4ebd935ab59ebe63306.png) (άτοπο)
(άτοπο) Aν
Aν ![\displaystyle{\sqrt[3]{2}\notin \mathbb Q} \displaystyle{\sqrt[3]{2}\notin \mathbb Q}](/forum/ext/geomar/texintegr/latexrender/pictures/92f4ab2f16cd8e808d44600ec8028868.png)