1. Θεωρούμε την πρόοδο
 και την χωρίζουμε σε ομάδες
και την χωρίζουμε σε ομάδες  έτσι ώστε η πρώτη να περιέχει
έτσι ώστε η πρώτη να περιέχει  όρο, η δεύτερη
όρο, η δεύτερη  , η τρίτη
, η τρίτη  , και ούτω καθ' εξής, η
, και ούτω καθ' εξής, η  -ιοστή να περιέχει
-ιοστή να περιέχει  όρους. Να βρεθεί το άθροισμα των όρων της
όρους. Να βρεθεί το άθροισμα των όρων της  -ιοστής ομάδας.
-ιοστής ομάδας.2. Δίνεται η εξίσωση
 . Για ποιες τιμές του
. Για ποιες τιμές του  η εξίσωση έχει πραγματικές ρίζες; Στην περίπτωση αυτή να υποθέσετε οτι οι πραγματικές ρίζες είναι
η εξίσωση έχει πραγματικές ρίζες; Στην περίπτωση αυτή να υποθέσετε οτι οι πραγματικές ρίζες είναι  και
και  όπου
όπου  . Ζητείται να βρεθεί το άθροισμα
. Ζητείται να βρεθεί το άθροισμα  . Αφού αποδείξετε οτι υπάρχουν μόνο δυο τιμές για το
. Αφού αποδείξετε οτι υπάρχουν μόνο δυο τιμές για το  , να διερευνήσετε για ποιες τιμές του
, να διερευνήσετε για ποιες τιμές του  παίρνει την μία τιμή και για ποιες την άλλη.
παίρνει την μία τιμή και για ποιες την άλλη.3. Εαν οι διαφορετικοί μεταξύ τους αριθμοί
 επαληθεύουν τις σχέσεις
επαληθεύουν τις σχέσεις  , να δειχθεί οτι καθεμία από τις παραστάσεις
, να δειχθεί οτι καθεμία από τις παραστάσεις  ισούται με
ισούται με 
4. Εαν
 είναι ρίζα της εξίσωσης
είναι ρίζα της εξίσωσης  και είναι
και είναι  , να δειχθεί τότε οτι θα είναι πάντα
, να δειχθεί τότε οτι θα είναι πάντα 

 το οποίο είναι τριώνυμο και έχει πραγματικές ρίζες όταν
το οποίο είναι τριώνυμο και έχει πραγματικές ρίζες όταν  δηλαδή έχει ρίζες για
δηλαδή έχει ρίζες για 
 και από το γεγονός ότι οι
και από το γεγονός ότι οι  είναι ρίζες , άρα από
είναι ρίζες , άρα από  έχουμε:
έχουμε: και
και
 δίνει:
δίνει: όπου
όπου  .
. και επειδή
και επειδή  είναι
είναι  ή
ή  .
. και (β)
και (β)  .
. αύριο... !!
αύριο... !!
 και
και 
 . Τότε έχουμε:
. Τότε έχουμε:  αυτή όμως είναι αμφινοσήμαντη τιμή αφού η
αυτή όμως είναι αμφινοσήμαντη τιμή αφού η  είναι γνήσια αύξουσα στο πεδίο ορισμού της..
είναι γνήσια αύξουσα στο πεδίο ορισμού της.. ...
...  πόσες λύσεις έχει;
πόσες λύσεις έχει;
 έχει άπειρες λύσεις , τις
έχει άπειρες λύσεις , τις  με
με 
 , αν περιορίσω τις τιμές του
, αν περιορίσω τις τιμές του  τέμνει άπειρες φορές την οριζόντια ευθεία
τέμνει άπειρες φορές την οριζόντια ευθεία 
 δεν είναι ισοδύναμες γιατί έχουν διαφορετικά πεδία ορισμού,
δεν είναι ισοδύναμες γιατί έχουν διαφορετικά πεδία ορισμού,  , είναι ισοδύναμη η 1η εξίσωση με την 2η
, είναι ισοδύναμη η 1η εξίσωση με την 2η  η ακολουθία των πρώτων όρων των ομάδων στις οποίες χωρίστηκε η πρόοδος.
η ακολουθία των πρώτων όρων των ομάδων στις οποίες χωρίστηκε η πρόοδος. το πλήθος , ισότητες:
το πλήθος , ισότητες:




 , προκύπτει ότι
, προκύπτει ότι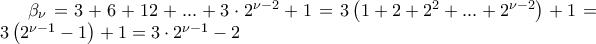
 όρων αριθμητικής προόδου με πρώτο όρο το
όρων αριθμητικής προόδου με πρώτο όρο το 



 μπορώ ισοδύναμα να γράψω ότι ισχύει
μπορώ ισοδύναμα να γράψω ότι ισχύει
 προκύπτει ισοδύναμα
προκύπτει ισοδύναμα
 προκύπτει ισοδύναμα
προκύπτει ισοδύναμα
 είναι παράμετρος. Ισοδύναμα λοιπόν η ορίζουσα του συστήματος είναι ίση με
είναι παράμετρος. Ισοδύναμα λοιπόν η ορίζουσα του συστήματος είναι ίση με  . Για να μη σας κουράζω με πράξεις , αυτό ισοδυναμεί με
. Για να μη σας κουράζω με πράξεις , αυτό ισοδυναμεί με  .
. και
και  .
. το σύστημα γράφεται
το σύστημα γράφεται 


 όπου
όπου  οποιοσδήποτε πραγματικός αριθμός.
οποιοσδήποτε πραγματικός αριθμός. το σύστημα γράφεται
το σύστημα γράφεται 






 .
.
 είναι ρίζες της εξίσωσης
είναι ρίζες της εξίσωσης 



 , ότι
, ότι 
![\displaystyle u=x^{2}+y^{2}+xy=\frac{1}{2}\left(2x^{2}+2y^{2}+2xy \right)=\frac{1}{2}\left[x^{2}+y^{2}+\left(x+y \right)^{2} \right]= \displaystyle u=x^{2}+y^{2}+xy=\frac{1}{2}\left(2x^{2}+2y^{2}+2xy \right)=\frac{1}{2}\left[x^{2}+y^{2}+\left(x+y \right)^{2} \right]=](/forum/ext/geomar/texintegr/latexrender/pictures/cf64de00b5cc04e2ae88f04eb952447c.png)
![\displaystyle \frac{1}{2}\left[x^{2}+y^{2}+\left(-z \right)^{2} \right]=\frac{1}{2}\left(x^{2}+y^{2}+z^{2} \right) \displaystyle \frac{1}{2}\left[x^{2}+y^{2}+\left(-z \right)^{2} \right]=\frac{1}{2}\left(x^{2}+y^{2}+z^{2} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/75103847573958e087e85ec0416db52f.png)
 ,
, και αφού κοιτάξω πότε μηδενίζονται οι
και αφού κοιτάξω πότε μηδενίζονται οι  τότε αντικαθιστώ ...
τότε αντικαθιστώ ... .
.  θεωρούμε την ευθεία
θεωρούμε την ευθεία  με εξίσωση
με εξίσωση  . Η (1) δηλώνει ότι τα σημεία
. Η (1) δηλώνει ότι τα σημεία  είναι και τα τρία σημεία της
είναι και τα τρία σημεία της 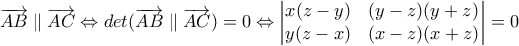
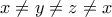 , με πολύ εύκολες πράξεις προκύπτει αμέσως ότι:
, με πολύ εύκολες πράξεις προκύπτει αμέσως ότι:  . Αφού όμως
. Αφού όμως  θα είναι:
θα είναι:  . Αντίστοιχα παίρνουμε και
. Αντίστοιχα παίρνουμε και  ,
,  .
.  (π.χ. από (2): αν ήταν
(π.χ. από (2): αν ήταν  , τότε θα ήταν
, τότε θα ήταν  , οπότε για να ισχύουν οι (3) και (4) θα έπρεπε
, οπότε για να ισχύουν οι (3) και (4) θα έπρεπε  άτοπο).
άτοπο).![k=x^2+y^2+xy= \frac{1}{2} \left(2x^2+2y^2+2xy) = \frac{1}{2} \left[ (x^2+y^2+(x+y)^2 \right] = \frac{1}{2} (x^2+y^2+z^2 ) k=x^2+y^2+xy= \frac{1}{2} \left(2x^2+2y^2+2xy) = \frac{1}{2} \left[ (x^2+y^2+(x+y)^2 \right] = \frac{1}{2} (x^2+y^2+z^2 )](/forum/ext/geomar/texintegr/latexrender/pictures/27fa27c563dd1bad33b4f7265df55e60.png)