1. Θεωρούμε το διώνυμο
 , όπου
, όπου  σταθερά
σταθερά  και συμβολίζουμε με
και συμβολίζουμε με  το πολυώνυμο
το πολυώνυμο  , δηλαδή αυτό που προκύπτει από το
, δηλαδή αυτό που προκύπτει από το 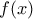 εαν σε αυτό το
εαν σε αυτό το  αντικατασταθεί με το
αντικατασταθεί με το 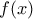 και ανάλογα με
και ανάλογα με  συμβολίζουμε το
συμβολίζουμε το  . Με την υπόθεση οτι κάθε ρίζα
. Με την υπόθεση οτι κάθε ρίζα  της εξίσωσης
της εξίσωσης  είναι απλή, οτι δηλαδή το πολυώνυμο
είναι απλή, οτι δηλαδή το πολυώνυμο  διαιρείται από το
διαιρείται από το  όχι όμως από το
όχι όμως από το  , να δείξετε οτι
, να δείξετε οτια) το
 διαιρείται από το
διαιρείται από το  και να βρείτε το πηλίκο
και να βρείτε το πηλίκο  της εν λόγω διαίρεσης
της εν λόγω διαίρεσηςβ) εαν
 είναι ρίζα της εξίσωσης
είναι ρίζα της εξίσωσης  , τότε και οι
, τότε και οι  είναι ρίζες της ίδιας εξίσωσης
είναι ρίζες της ίδιας εξίσωσηςγ) εξίσωση με ρίζες τις
 είναι η
είναι η  .
. Τέλος παριστάνοντας με
 ρίζα του
ρίζα του  διάφορου των
διάφορου των  , τότε σύμφωνα με τα παραπάνω και οι
, τότε σύμφωνα με τα παραπάνω και οι  είναι ρίζες του
είναι ρίζες του  και θέτοντας
και θέτοντας  , να βρείτε οτι τα
, να βρείτε οτι τα  και
και  είναι ρίζες της εξίσωσης
είναι ρίζες της εξίσωσης 
2. Η τετραγωνική ρίζα μιγαδικού αριθμού
 έχει πάντοτε δυο τιμές αντίθετες. Από αυτές επιλέγουμε εδώ εκείνη την οποία , στην περίπτωση που το πραγματικό της μέρος είναι διάφορο του μηδενός έχει πραγματικό μέρος θετικό, ενώ στην περίπτωση που το πραγματικό της μέρος είναι μηδέν, έχει συντελεστή του
έχει πάντοτε δυο τιμές αντίθετες. Από αυτές επιλέγουμε εδώ εκείνη την οποία , στην περίπτωση που το πραγματικό της μέρος είναι διάφορο του μηδενός έχει πραγματικό μέρος θετικό, ενώ στην περίπτωση που το πραγματικό της μέρος είναι μηδέν, έχει συντελεστή του  θετικό. Να λύσετε σύμφωνα με την παραπάνω συμφωνία , τις δυο παρακάτω εξισώσεις :
θετικό. Να λύσετε σύμφωνα με την παραπάνω συμφωνία , τις δυο παρακάτω εξισώσεις :  , και να βρείτε , εαν αυτές έχουν κοινή ρίζα.
, και να βρείτε , εαν αυτές έχουν κοινή ρίζα.Να κάνετε το ίδιο για τις εξισώσεις
 .
.3. Θεωρούμε ακολουθία αριθμών
 των οποίων οι όροι πληρούν τις σχέσεις
των οποίων οι όροι πληρούν τις σχέσεις  για φυσικό
για φυσικό  , παραλείποντας την τετριμμένη περίπτωση όπου όλοι οι όροι είναι ίσοι με μηδέν. Όπως είναι φυσικό, και η ακολουθία
, παραλείποντας την τετριμμένη περίπτωση όπου όλοι οι όροι είναι ίσοι με μηδέν. Όπως είναι φυσικό, και η ακολουθία  για τυχαίο αριθμό
για τυχαίο αριθμό  , ονομαζόμενη ανάλογη της πρώτης, πληρεί τις παραπάνω σχέσεις (υποτίθεται
, ονομαζόμενη ανάλογη της πρώτης, πληρεί τις παραπάνω σχέσεις (υποτίθεται  ) . Να δείξετε οτι
) . Να δείξετε οτια) για οποιεσδήποτε ορισμένες μη ανάλογες ακολουθίες
 και
και  , τυχαία άλλη ακολουθία που ικανοποιεί επίσης τις παραπάνω σχέσεις, είναι της μορφής
, τυχαία άλλη ακολουθία που ικανοποιεί επίσης τις παραπάνω σχέσεις, είναι της μορφής  (
( ) με
) με  κατάλληλους αριθμούς ανεξάρτητους του
κατάλληλους αριθμούς ανεξάρτητους του 
β) σαν παραπάνω μη ανάλογες ακολουθίες
 και
και  , μπορούμε να πάρουμε δυο γεωμετρικές προόδους με πρώτο όρο
, μπορούμε να πάρουμε δυο γεωμετρικές προόδους με πρώτο όρο  , των οποίων να υπολογίσετε τους λόγους
, των οποίων να υπολογίσετε τους λόγουςγ) για
 είναι
είναι  και
και ![\displaystyle{\gamma_{\nu}^3=\frac{1}{5} [\gamma_{3\nu}+(-1)^{\nu+1}3\gamma_{\nu}]} \displaystyle{\gamma_{\nu}^3=\frac{1}{5} [\gamma_{3\nu}+(-1)^{\nu+1}3\gamma_{\nu}]}](/forum/ext/geomar/texintegr/latexrender/pictures/f13944d69b5566f3ed5479434d33fec4.png) χρησιμοποιώντας τα προηγούμενα αποτελέσματα.
χρησιμοποιώντας τα προηγούμενα αποτελέσματα.Υ.Γ. Σχολιάζοντας την τεράστια έκταση του 1ου θέματος μεταξύ άλλων ο Πάλλας στο ετήσιο Δελτίο του σχολιάζει ''θα είμεθα ευτυχείς εαν ο κ. εξεταστής μας έλεγε πόσοι υποψήφιοι διεξήλθον κανονικά το θέμα. Ασφαλώς κατά την γνώμη μας ουδείς.''
edit
διόρθωση λέξης στο 2ο

 Έχουμε
Έχουμε 


 η εξίσωση γίνεται :
η εξίσωση γίνεται :  που ισχύει
που ισχύει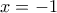 η εξίσωση γίνεται :
η εξίσωση γίνεται :  που δεν ισχύει
που δεν ισχύει
 η εξίσωση γίνεται :
η εξίσωση γίνεται :  που δεν ισχύει
που δεν ισχύει που ισχύει
που ισχύει
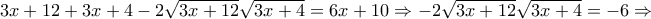

 που δεν ισχύει
που δεν ισχύει που ισχύει
που ισχύει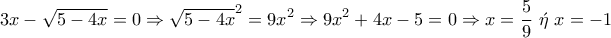
 που ισχύει
που ισχύει που δεν ισχύει
που δεν ισχύει