ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Παρ Νοέμ 24, 2023 7:49 pm
Δίνεται ημικύκλιο διαμέτρου
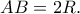
Φέρνουμε χορδή
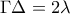
παράλληλη στην

Ζητείται να βρεθεί
α) ο όγκος που παράγεται από το μικτόγραμμο χωρίο
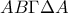
όταν περιστραφεί γύρω από την

β) ποια σχέση πρέπει να υπάρχει μεταξύ των

και

ώστε ο όγκος που παράγεται από το κυκλικό τμήμα
που αντιστοιχεί στο μικρό τόξο χορδής

να είναι το μισό του όγκου που παράγεται από το ημικύκλιο, όταν περιστραφούν
και τα δύο γύρω από την
 Κάθε τεκμηριωμένη λύση γίνεται δεκτή. Αυτό ίσχυε και το 1948, ισχύει και τώρα...
Κάθε τεκμηριωμένη λύση γίνεται δεκτή. Αυτό ίσχυε και το 1948, ισχύει και τώρα...
Θεωρούμε ένα ορθοκανονικό σύστημα συντεταγμένων στον χώρο με αρχή των αξόνων το κέντρο του κύκλου και άξονα

την ευθεία

. Θα βρούμε αρχικά τον όγκο
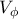
, που παράγεται από το κυκλικό τμήμα που αντιστοιχεί στο έλλασον τόξο της χορδής

όταν αυτό περιστραφεί γύρο από τον άξονα

.
Η εξίσωση του τόξου

δίνεται από την συνάρτηση
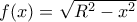
και η εξίσωση της χορδής

από την σταθερή συνάρτηση
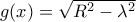
. Οπότε ο ζητούμενος όγκος θα δίνεται από το ολοκλήρωμα
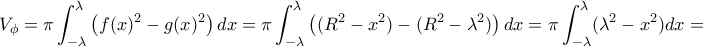
![\displaystyle{= \pi \left ( \lambda^2 \left [ x \right ]_{-\lambda}^{\lambda} -\left [ \dfrac{x^3}{3} \right ]_{-\lambda}^{\lambda} \right )=\pi \left ( 2\lambda^3 -\dfrac{2}{3} \lambda^3 \right ) = \dfrac{4}{3} \pi \lambda^3} \displaystyle{= \pi \left ( \lambda^2 \left [ x \right ]_{-\lambda}^{\lambda} -\left [ \dfrac{x^3}{3} \right ]_{-\lambda}^{\lambda} \right )=\pi \left ( 2\lambda^3 -\dfrac{2}{3} \lambda^3 \right ) = \dfrac{4}{3} \pi \lambda^3}](/forum/ext/geomar/texintegr/latexrender/pictures/f8bfbff0263f7b8a12d76764b5a17f1d.png)
Επομένος για να είναι αυτός ο όγκος ο μισός του όγκου του ημικύκλιου όταν αυτό περιστραφεί (σφαίρα ακτίνας

) θα πρέπει
![\dfrac{4}{3} \pi \lambda^3 = \dfrac{1}{2} \cdot \dfrac{4}{3} \pi R^3 \Rightarrow \lambda = \dfrac{R}{\sqrt[3]{2}} \dfrac{4}{3} \pi \lambda^3 = \dfrac{1}{2} \cdot \dfrac{4}{3} \pi R^3 \Rightarrow \lambda = \dfrac{R}{\sqrt[3]{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/fafb1cfdc6b6277d530d4e185ec45825.png)
.
Ο δε όγκος

, που παράγει το μικτόγραμμο χωρίο
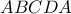
όταν περιστραφεί γύρο από την ευθεία

, θα είναι
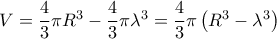
.

- emp_1948.png (600.75 KiB) Προβλήθηκε 1145 φορές
Συμπέρασμα: προσοχή σε κοσμηματοπώλη που προσπαθεί να πουλήσει ένα δαχτυλίδι σε μεγαλύτερη τιμή, μόνο και μόνο, επειδή φαίνεται μεγαλύτερο.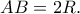 Φέρνουμε χορδή
Φέρνουμε χορδή 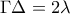 παράλληλη στην
παράλληλη στην 
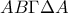 όταν περιστραφεί γύρω από την
όταν περιστραφεί γύρω από την 
 και
και  ώστε ο όγκος που παράγεται από το κυκλικό τμήμα
ώστε ο όγκος που παράγεται από το κυκλικό τμήμα  να είναι το μισό του όγκου που παράγεται από το ημικύκλιο, όταν περιστραφούν
να είναι το μισό του όγκου που παράγεται από το ημικύκλιο, όταν περιστραφούν 
 αντί
αντί  στο β).
στο β).
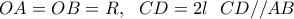
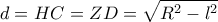
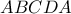 , γύρω από τον άξονα που ορίζει η διάμετρος
, γύρω από τον άξονα που ορίζει η διάμετρος  προκύπτει:
προκύπτει: 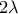 ( ό όγκος του σχήματος εκ περιστροφής που προκύπτει από την καμπύλη
( ό όγκος του σχήματος εκ περιστροφής που προκύπτει από την καμπύλη 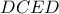 στο σχήμα του κ. Κώστα στην προηγούμενη δημοσίευση), είναι ανεξάρτητος της ακτίνας της σφαίρας και δίνεται από την σχέση
στο σχήμα του κ. Κώστα στην προηγούμενη δημοσίευση), είναι ανεξάρτητος της ακτίνας της σφαίρας και δίνεται από την σχέση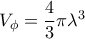
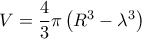 .
.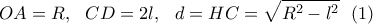
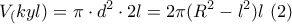
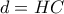 και ύψος το
και ύψος το 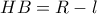 είναι:
είναι:

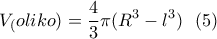
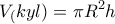
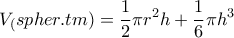
 την ευθεία
την ευθεία 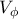 , που παράγεται από το κυκλικό τμήμα που αντιστοιχεί στο έλλασον τόξο της χορδής
, που παράγεται από το κυκλικό τμήμα που αντιστοιχεί στο έλλασον τόξο της χορδής  όταν αυτό περιστραφεί γύρο από τον άξονα
όταν αυτό περιστραφεί γύρο από τον άξονα 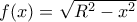 και η εξίσωση της χορδής
και η εξίσωση της χορδής 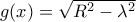 . Οπότε ο ζητούμενος όγκος θα δίνεται από το ολοκλήρωμα
. Οπότε ο ζητούμενος όγκος θα δίνεται από το ολοκλήρωμα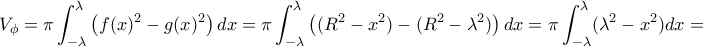
![\displaystyle{= \pi \left ( \lambda^2 \left [ x \right ]_{-\lambda}^{\lambda} -\left [ \dfrac{x^3}{3} \right ]_{-\lambda}^{\lambda} \right )=\pi \left ( 2\lambda^3 -\dfrac{2}{3} \lambda^3 \right ) = \dfrac{4}{3} \pi \lambda^3} \displaystyle{= \pi \left ( \lambda^2 \left [ x \right ]_{-\lambda}^{\lambda} -\left [ \dfrac{x^3}{3} \right ]_{-\lambda}^{\lambda} \right )=\pi \left ( 2\lambda^3 -\dfrac{2}{3} \lambda^3 \right ) = \dfrac{4}{3} \pi \lambda^3}](/forum/ext/geomar/texintegr/latexrender/pictures/f8bfbff0263f7b8a12d76764b5a17f1d.png)
![\dfrac{4}{3} \pi \lambda^3 = \dfrac{1}{2} \cdot \dfrac{4}{3} \pi R^3 \Rightarrow \lambda = \dfrac{R}{\sqrt[3]{2}} \dfrac{4}{3} \pi \lambda^3 = \dfrac{1}{2} \cdot \dfrac{4}{3} \pi R^3 \Rightarrow \lambda = \dfrac{R}{\sqrt[3]{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/fafb1cfdc6b6277d530d4e185ec45825.png) .
. , που παράγει το μικτόγραμμο χωρίο
, που παράγει το μικτόγραμμο χωρίο  όταν περιστραφεί γύρο από την ευθεία
όταν περιστραφεί γύρο από την ευθεία 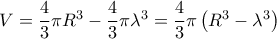 .
. .
.
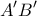 το μήκος της
το μήκος της 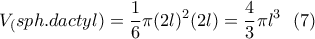
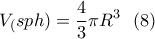
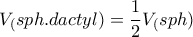
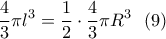
![\displaystyle{l=\frac{R}{\sqrt[3]{2}} \ \ (10) } \displaystyle{l=\frac{R}{\sqrt[3]{2}} \ \ (10) }](/forum/ext/geomar/texintegr/latexrender/pictures/ab3bfa4b44a51ac807207d09b10b851f.png)
![\displaystyle{R=l \sqrt[3]{2} \ \ (11) } \displaystyle{R=l \sqrt[3]{2} \ \ (11) }](/forum/ext/geomar/texintegr/latexrender/pictures/ee743d62fcb9bf842537718eb104d689.png)
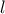 που βρέθηκε από την (10) ικανοποιεί την πρόταση:
που βρέθηκε από την (10) ικανοποιεί την πρόταση: από τα κέντρα των σφαιρών (αριστερά ακτίνας
από τα κέντρα των σφαιρών (αριστερά ακτίνας 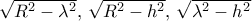 , αντίστοιχα.
, αντίστοιχα. 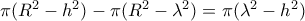 και ο κύκλος δεξιά
και ο κύκλος δεξιά 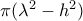 , δηλαδή ίσο με το δακτυλίδι.
, δηλαδή ίσο με το δακτυλίδι.