Τα συγκεκριμένα είναι από τις εξετάσεις Ιουνίου της κεντρικής ζώνης ώρας.
Ομάδα Β
B1. Ένα δισκίο φαρμάκου ζυγίζει 70 mg και περιέχει 4% δραστικής ουσίας. Για βρέφος μέχρι 6 μηνών ο γιατρός χορηγεί 1,05 mg δραστικής ουσίας για κάθε κιλό του βάρους του το εικοσιτετράωρο. Πόσα δισκία αυτού του φαρμάκου πρέπει να χορηγηθούν σε βρέφος 5 μηνών που ζυγίζει 8 κιλά κατά την διάρκεια του εικοσιτετράωρου.
B2. Στο διάγραμμα απεικονίζονται οι εξαγωγές χαλκού για δέκα χώρες (σε χιλιάδες τόνους) για το 2006. Μεταξύ των χωρών του πίνακα οι ΗΠΑ κατέχουν την πρώτη θέση. Ποια θέση κατέχει ο Καναδάς; Οι χώρες από αριστερά προς δεξιά είναι (Αυστραλία, Ζάμπια, Ινδονησία, Καζακστάν, Καναδάς, Κίνα, Περού, Πολωνία, Ρωσία, ΗΠΑ.
B3. Να βρεθεί το εμβαδόν του τραπεζίου του σχήματος
B4. Ανεξάρτητο πειραματικό εργαστήριο προσδιορίζει την βαθμολόγηση
 (κατάταξη) οικιακών συσκευών με βάση το συντελεστή τιμής, που ισούται με 0,01 της μέσης τιμής κόστους
(κατάταξη) οικιακών συσκευών με βάση το συντελεστή τιμής, που ισούται με 0,01 της μέσης τιμής κόστους  , τον δείκτη εργονομικότητας
, τον δείκτη εργονομικότητας  , ποιότητας
, ποιότητας  και σχεδίασης
και σχεδίασης  . Ο καθένας από του δείκτες έχει τιμή έναν ακέραιο αριθμό από το 0 έως το 4. Η τελική βαθμολόγηση υπολογίζεται από τον τύπο
. Ο καθένας από του δείκτες έχει τιμή έναν ακέραιο αριθμό από το 0 έως το 4. Η τελική βαθμολόγηση υπολογίζεται από τον τύπο
Στον πίνακα δίνονται η μέση τιμή κόστους και οι τιμές για το κάθε δείκτη μερικών ηλεκτρικών βραστήρων. Προσδιορίστε την μεγαλύτερη βαθμολόγηση των βραστήρων που παρουσιάζονται στον πίνακα.
B5. Να βρεθεί η ρίζα της εξίσωσης

B6. Στο τρίγωνο
 είναι
είναι  ,
,  και το ύψος
και το ύψος  είναι ίσο με 8. Να βρείτε το συνημίτονο της γωνίας
είναι ίσο με 8. Να βρείτε το συνημίτονο της γωνίας  .
.B7. Να βρείτε την τιμή της παράστασης
 .
.B8. Στο σχήμα έχουμε την γραφική παράσταση της συνάρτησης
 στο διάστημα
στο διάστημα  . Να βρείτε τον αριθμό των σημείων στα οποία η παράγωγος της
. Να βρείτε τον αριθμό των σημείων στα οποία η παράγωγος της  είναι ίση με 0.
είναι ίση με 0. Β9. Κώνος είναι εγγεγραμμένος σε σφαίρα. Το κέντρο της σφαίρας συμπίπτει με το κέντρο της βάσης του κώνου. Η ακτίνα της σφαίρας είναι ίση με
 . Να βρείτε το μήκος της γενέτειρας του κώνου.
. Να βρείτε το μήκος της γενέτειρας του κώνου. B10. Πριν από την πρώτη φάση ενός τουρνουά τένις τους συμμετέχοντες τους χωρίζουν σε ζευγάρια αγώνων με τυχαίο τρόπο μέσο κλήρωσης. Συνολικά στο τουρνουά συμμετέχουν 76 τενίστες, απο τους οποίους 7 είναι ευρωπαίοι μεταξύ αυτών και ο Μάρκος Παγδατής. Να βρείτε την πιθανότητα ο Μάρκος Παγδατής να είναι αντίπαλος με κάποιον άλλο ευρωπαίο τενίστα στη πρώτη φάση του τουρνουά.
Β11. Να βρείτε τον όγκο κανονικού εξαγωνικού πρίσματος με εμβαδόν βάσης 12 και πλευρική ακμή ίση με 2.
Β12. Ανιχνευτής βαθυσκάφους που βυθίζεται κατακόρυφα ομαλά προς τον βυθό, στέλνει παλμούς υπερήχων συχνότητας 217 MHz. Η ταχύτητα βύθισης του βαθυσκάφους δίνεται από την σχέση
 , όπου
, όπου  η ταχύτητα του ήχου στο νερό,
η ταχύτητα του ήχου στο νερό,  η συχνότητα των παλμών που εκπέμπονται (σε MHz),
η συχνότητα των παλμών που εκπέμπονται (σε MHz),  η συχνότητα του ανακλώμενου σήματος από τον πυθμένα που λαμβάνει ο δέκτης(σε MHz). Να προσδιορίσετε την μέγιστη δυνατή συχνότητα
η συχνότητα του ανακλώμενου σήματος από τον πυθμένα που λαμβάνει ο δέκτης(σε MHz). Να προσδιορίσετε την μέγιστη δυνατή συχνότητα  του ανακλώμενου σήματος, αν η ταχύτητα βύθισης του βαθυσκάφους δεν πρέπει να υπερβαίνει τα 12 m/sec. Υπολογίστε το αποτέλεσμα σε MHz .
του ανακλώμενου σήματος, αν η ταχύτητα βύθισης του βαθυσκάφους δεν πρέπει να υπερβαίνει τα 12 m/sec. Υπολογίστε το αποτέλεσμα σε MHz .B13. Ένα κανό καγιάκ αναχώρησε από το σημείο Α στις 10:00 η ώρα με προορισμό το σημείο Β σε απόσταση 15 χμ από το Α. Ύστερα από διάλλειμα μιας ώρα και είκοσι λεπτών στο Β, ξεκίνησε για την επιστροφή στο σημείο Α στο οποίο έφτασε στις 16:00 η ώρα της ίδιας μέρας. Να προσδιορίσετε (σε χμ/ώρα) την ιδία ταχύτητα του κανό, αν είναι γνωστό ότι η ταχύτητα ροής του ποταμού είναι 2χμ/ώρα.
B14. Να βρείτε την ελάχιστη τιμή της συνάρτησης
 στο διάστημα
στο διάστημα ![[2,32] [2,32]](/forum/ext/geomar/texintegr/latexrender/pictures/4bddbb2bfc50f9e95ebfd744232ce873.png) .
.Ομάδα C
C1. α) Να λύσετε την εξίσωση
 .
.β) Να βρέιτε όλες τις ρίζες αυτής της εξίσωσης στο διάστημα
![\displaystyle{ [5 \pi , \frac{13 \pi}{2}] } \displaystyle{ [5 \pi , \frac{13 \pi}{2}] }](/forum/ext/geomar/texintegr/latexrender/pictures/2c4d41c95a1fb1a3de17ba7911bdf895.png) .
.C2. Στην κανονική τετραγωνική πυραμίδα
 με κορυφή το σημείο
με κορυφή το σημείο  οι πλευρές της βάσης έχουν μήκος 6 και οι παράπλευρες ακμές μήκος ίσο με 12. Να βρείτε το εμβαδόν τομής της πυραμίδας με το επίπεδο που διέρχεται από το σημείο
οι πλευρές της βάσης έχουν μήκος 6 και οι παράπλευρες ακμές μήκος ίσο με 12. Να βρείτε το εμβαδόν τομής της πυραμίδας με το επίπεδο που διέρχεται από το σημείο  και το μέσο της ακμής
και το μέσο της ακμής  και είναι παράλληλο με την ευθεία
και είναι παράλληλο με την ευθεία  .
.C3. Να λύσετε το σύστημα των ανισώσεων
 ,
, .
.C4. Κύκλοι με ακτίνες
 και
και  και κέντρα
και κέντρα  και
και  αντίστοιχα εφάπτονται στο σημείο
αντίστοιχα εφάπτονται στο σημείο  . Ευθεία που διέρχεται από το σημείο
. Ευθεία που διέρχεται από το σημείο  τέμνει σε ένα δευτερο σημείο
τέμνει σε ένα δευτερο σημείο  τον μικρότερο κύκλο και σε σημείο
τον μικρότερο κύκλο και σε σημείο  τον μεγαλύτερο. Να βρείτε το εμβαδόν του τριγώνου
τον μεγαλύτερο. Να βρείτε το εμβαδόν του τριγώνου  , αν
, αν  .
.C5. Να βρείτε όλες τις τιμές του
 , για τις οποίες η εξίσωση
, για τις οποίες η εξίσωση
έχει μοναδική ρίζα.
C6. Θεωρούμε (σκέφτομαστε) κάποιους φυσικούς αριθμούς (όχι απαραίτητα διαφορετικούς). Αυτοί οι αριθμοί και όλα τα δυνατά αθροίσματά τους ( ανά δύο, ανα τρία κτλ.) γράφονται στο πίνακα κατά αύξουσα σειρά. Αν κάποιος αριθμός
 , που έχει γραφτεί στο πίνακα, επαναλαμβάνεται κάποσες φορές, τότε στον πίνακα παραμένει μόνο ένας τέτοιος
, που έχει γραφτεί στο πίνακα, επαναλαμβάνεται κάποσες φορές, τότε στον πίνακα παραμένει μόνο ένας τέτοιος  και οι υπόλοιποι αριθμοί που ισούνται με το
και οι υπόλοιποι αριθμοί που ισούνται με το  σβήνονται. Για παράδειγμα αν σκεφτήκαμε τους αριθμούς
σβήνονται. Για παράδειγμα αν σκεφτήκαμε τους αριθμούς  , τότε στον πίνακα θα είναι γραμμένοι οι αριθμοί
, τότε στον πίνακα θα είναι γραμμένοι οι αριθμοί  .
.α) Να βρείτε παράδειγμα τέτοιων αριθμών ώστε στο πίνακα να γραφτούν οι αριθμοί

β) Υπάρχει άραγε παράδειγμα τέτοιων αριθμών ώστε στον πίνακα να έχουμε τους αριθμούς
 ;
;γ) Βρείτε όλα τα παραδείγματα αριθμών που μπορούμε να σκεφτούμε για τους οποίους στον πίνακα θα γραφτούν οι αριθμοί
 .
.Κάποια πληροφοριακά στοιχεία για τον τρόπο εξέτασης και βαθμολόγησης.
Υγ1. Δεν υπάρχουν θέματα Α ομάδας στην εξέταση των μαθηματικών. Α ομάδας είναι θέματα πολλαπλής επιλογής που χρησιμοποιούνται σε άλλα μαθήματα. Χρόνος εξέτασης 235 λεπτά.
Υγ2. Σε κάθε θεμα της Β ομάδας πρέπει να δωθεί μόνο το τελικό αποτέλεσμα. Στα θέματα αυτά αντιστοιχεί ένα 1 μόριο ανά θέμα. Δηλαδή για την συγκεκριμένη εξέταση 14 μόρια συνολικά.
Στα θέματα C1, C2 αντιστοιχούν 2 μόρια στο καθένα, στα C3,C4 αντιστοιχούν 3 μόρια στο καθενα και στα C5,C6 4 μόρια στο καθένα. Το πόσα θέματα Β ομάδας και πόσα C ομάδας θα υπάρχουν μπορεί να μεταβάλεται ανά χρονιά. Συνήθως είναι 12-15 Β όμαδας και 6-7 C Ομάδας. Τα παραπάνω μόρια ονομάζονται πρωτεύοντα μόρια (ΠΜ). Σύνολο για αυτή τη χρονιά 32 πρωτεύοντα μόρια.
Υγ3. Για να έχει ο εξεταζόμενος την δυνατότητα να συμμετάσχει στην διαδικασία εισαγωγής σε πανεπιστήμιο θα πρέπει να έχει πάρει κάποιο ελάχιστο αριθμό μορίων(βάση). Ο αριθμός αυτός μεταβάλεται κάθε χρονιά και εξαρτάται από τα στατιστικά αποτέλεσματα όλων των εξεταζόμενων, από τα αποτελεσματα προηγούμενων χρονιών, από τις εισηγήσεις των επιτροπών θεμάτων για την δυσκολία τους και την κατανομή των μορίων ανά γνωστικό αντικέιμενο( Γεωμετρία,Άλγεβρα, Ανάλυση, κτλ). Η διαδικασία αυτή γίνεται από ειδικό λογισμικό.
Με την παραπάνω διαδικασία υπολογίζονται δυο όρια πρωτεύοντων μορίων, το πρώτο ΠΜ1 αντιστοιχεί σε αυτό που καλείτε στοιχειώδης γνώση μαθηματικών. Το δεύτερο ΠΜ2 είναι το όριο που αντιστοιχεί στην ικανοποιητική γνώση των μαθηματικών. Με δεδομένο τα παραπάνω όρια γίνεται η αντιστοίχηση των μορίων στα 100. Μηδέν πρωτεύοντα -> 0/100, 32 πρωτεύοντα μόρια -> 100/100. Η αντιστοίχηση δεν είναι γραμμική αλλά κατά τμήματα γραμμική ανάμεσα στα παραπάνω όρια. Με μεγαλύτερη κλίση μέχρι το ΠΜ1 και μετά το ΠΜ2 και μικρότερη κλίση μεταξύ του ΠΜ1 και ΠΜ2. μεταξύ των παραπάνω σημείων η αντιστοίχηση είναι γραμμική στο πλησέστερο ακέραιο.
Για την συγκεκριμένη χρονιά τα πρωτεύοντα μόρια της βάσης ΠΜ1 ήταν 5 και αντιστοιχούσαν σε 24/100.
Για το ΠΜ2 ήταν 15 και αντιστοιχούσαν σε 63/100.
Υγ4. Οι επιδώσεις στα παραπάνω θέματα διαμορφώθηκαν ως εξής:
0-10: 3,5%;
11-20: 2,7%;
21-30: 10,5%;
31-40: 18,6%;
41-50: 13%;
51-60: 26,4%;
61-70: 17,3%;
71-80: 5,1%;
81-90: 2,2%;
91-100: 0,7%.








 ,
,  και
και 
 , τότε προκύπτει ότι
, τότε προκύπτει ότι  και
και  που είναι άτοπο.
που είναι άτοπο.
 , η δεύτερη ανίσωση γράφεται:
, η δεύτερη ανίσωση γράφεται:
![\boxed{x \in ( - \infty , - 3] \cup \left\{ 0 \right\} \cup [1,4)} \boxed{x \in ( - \infty , - 3] \cup \left\{ 0 \right\} \cup [1,4)}](/forum/ext/geomar/texintegr/latexrender/pictures/0b7fffe384e7ddd2265a02d88cfddd83.png)

 :
: 


 είναι ισοσκελή με πλευρές αντίστοιχα
είναι ισοσκελή με πλευρές αντίστοιχα  και προσκείμενες στην βάση
και προσκείμενες στην βάση 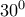
![(BCO_{2}) = [(BO_{1}O_{2}) - (BO_{1}A) ]+ (CO_{2}A) (BCO_{2}) = [(BO_{1}O_{2}) - (BO_{1}A) ]+ (CO_{2}A)](/forum/ext/geomar/texintegr/latexrender/pictures/69bc586d59392eb72d2d70bbf841ef94.png)
![(BCO_{2}) = \frac{\sin {120^0}}{2}[r_{1}(r_{1}+r_{2}) - r_{1}^{2}+ r_{2}^{2}] (BCO_{2}) = \frac{\sin {120^0}}{2}[r_{1}(r_{1}+r_{2}) - r_{1}^{2}+ r_{2}^{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/b586813b58a821eb5b512e75107d6861.png)


![(BO_{2}C)= \frac{\sin{120^{0}}}{2}[r_{2}^{2} -r_{1}^{2}-r_{1}(r_{2}-r_{1})] (BO_{2}C)= \frac{\sin{120^{0}}}{2}[r_{2}^{2} -r_{1}^{2}-r_{1}(r_{2}-r_{1})]](/forum/ext/geomar/texintegr/latexrender/pictures/1f2cdde8192a75af0b2eae977b64c249.png)



 .
. με συντελεστή μεγιστοβάθμιου όρου το
με συντελεστή μεγιστοβάθμιου όρου το 
 , που θα δώσει
, που θα δώσει  , και διευθετούμε τις περιπτώσεις με
, και διευθετούμε τις περιπτώσεις με  κ.λπ.
κ.λπ. και προσθέτοντας ανά δύο τρείς, τέσσερις αριθμούς φτιάχνω τους
και προσθέτοντας ανά δύο τρείς, τέσσερις αριθμούς φτιάχνω τους 

 και φτιάχνω τους
και φτιάχνω τους 
 , και προσθέτοντας ανά δύο, τρεις κλπ φτιάχνω όλα τα δυνατά αθροίσματα
, και προσθέτοντας ανά δύο, τρεις κλπ φτιάχνω όλα τα δυνατά αθροίσματα  όπως παρακάτω:
όπως παρακάτω:
 (τρις)
(τρις) (τρις)
(τρις) (τρις)
(τρις) (τρις)
(τρις) (τρις)
(τρις) (τρις)
(τρις)
 (τρις)
(τρις)


 της ακμής
της ακμής  τέμνει και τις ακμές
τέμνει και τις ακμές  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα και η τομή του επιπέδου αυτού και της πυραμίδας είναι προφανώς τετράπλευρο και μάλιστα λόγω της κανονικότητας της πυραμίδας και της παραλληλίας του επιπέδου προς τηn
αντίστοιχα και η τομή του επιπέδου αυτού και της πυραμίδας είναι προφανώς τετράπλευρο και μάλιστα λόγω της κανονικότητας της πυραμίδας και της παραλληλίας του επιπέδου προς τηn  είναι παράλληλη της
είναι παράλληλη της 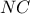 , δηλαδή το τετράπλευρο
, δηλαδή το τετράπλευρο  είναι χαρταετός Από τους επιμέρους -και εύκολους - υπολογισμούς που φαίνονται στα σχέδια μου έχουμε
είναι χαρταετός Από τους επιμέρους -και εύκολους - υπολογισμούς που φαίνονται στα σχέδια μου έχουμε  και
και 
 , άρα
, άρα 
 , οπότε
, οπότε 

![x \in [-7,-1] x \in [-7,-1]](/forum/ext/geomar/texintegr/latexrender/pictures/96d6f7e0fadbdc423b538c89364a87bf.png)
 ακτίνας
ακτίνας  .
. 

 , με
, με 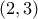
 στο σημείο
στο σημείο 
 (θετική κλίση για την ευθεία)
(θετική κλίση για την ευθεία)
 και αναγκαστικά θα έχει δύο κοινά σημεία με το ημικύκλιο.
και αναγκαστικά θα έχει δύο κοινά σημεία με το ημικύκλιο.  (1)
(1) που βρίσκεται -προφανώς-στον θετικό ημιάξονα και η ευθεία έχει αρνητική κλίση - αλλά δεν μας χρειάζονται αυτά)
που βρίσκεται -προφανώς-στον θετικό ημιάξονα και η ευθεία έχει αρνητική κλίση - αλλά δεν μας χρειάζονται αυτά)![x\in [-7,-1] x\in [-7,-1]](/forum/ext/geomar/texintegr/latexrender/pictures/e7c68ed59d61ee88fd5b52bff1d12330.png) ισχύει
ισχύει  (2)
(2)
 τότε έχουμε την ευθεία
τότε έχουμε την ευθεία 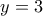

 , η προβολή της τομής
, η προβολή της τομής  στο επίπεδο της βάσης και τα διάφορα μεγέθη που χρειάζονται για την εύρεση του εμβαδού, τα οποία ήδη έχουν υπολογισθεί (δεν ήταν και κάτι δύσκολο
στο επίπεδο της βάσης και τα διάφορα μεγέθη που χρειάζονται για την εύρεση του εμβαδού, τα οποία ήδη έχουν υπολογισθεί (δεν ήταν και κάτι δύσκολο