gbaloglou έγραψε:gbaloglou έγραψε:Θα ήθελα απλώς να αναφέρω ότι, με βάση την παραπάνω δουλειά μου και κάποια 'πειράματα' ... είμαι πια σχεδόν σίγουρος ότι ούτε πέμπτου βαθμού SNS πολυώνυμο υπάρχει!
Πιο συγκεκριμένα, ΕΙΚΑΖΩ -- με στρατηγική που προς το παρόν αποτυγχάνει -- ότι η πρώτη εξίσωση του 3x3 συστήματος, δηλαδή η

δεν έχει πραγματικές λύσεις!
Ιδού η στρατηγική που όντως αποτυγχάνει --
χωρίς αυτό να σημαίνει ότι δεν ισχύει η παραπάνω εικασία! -- στην περίπτωση πολυωνύμου πέμπτου βαθμού: παρατίθεται εδώ ΚΑΙ επειδή επιτυγχάνει στα πολυώνυμα έκτου ή μεγαλύτερου βαθμού, επιλύοντας το SNS-6.2 (όπως δείχνω στην επόμενη δημοσίευση)!
Θεωρώντας την παραπάνω εξίσωση είτε ως δευτεροβάθμια ως προς

είτε ως δευτεροβάθμια ως προς

, συμπεραίνουμε ότι έχει πραγματικές λύσεις ως προς

,

,
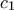
αν και μόνον αν είναι μη αρνητικές οι αντίστοιχες διακρίνουσες, δηλαδή αν και μόνον αν ισχύουν
ταυτόχρονα οι ανισότητες
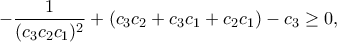

Η δεύτερη ανισότητα διακρίνουσας γράφεται και ως

, συνεπαγόμενη τις

,

,

. Ισχύοντας λοιπόν η δεύτερη ανισότητα διακρίνουσας ... δημιουργεί ελπίδες μη ισχύος της πρώτης ανισότητας διακρίνουσας ... καθώς οι μικρές σχετικά τιμές των

,

,
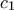
ΙΣΩΣ μεγαλώνουν υπερβολικά τον αρνητικό όρο

, κλπ κλπ
Ένας τρόπος πραγμάτωσης των παραπάνω, βασιζόμενος στην

, είναι ο εξής: χρησιμοποιώντας τις γνωστές ανισότητες

και

, καθώς και την δεύτερη ανισότητα διακρίνουσας στις μορφές

και

, συμπεραίνουμε ότι ισχύει η ανισότητα

ΑΝ τώρα ίσχυε, για

, και η

, ισοδύναμη προς την

για

,
ΤΟΤΕ θα είχαμε αποδείξει ότι η ισχύς της δεύτερης ανισότητας διακρίνουσας συνεπάγεται την μη ισχύ της πρώτης ανισότητας διακρίνουσας, και θα είχαμε πετύχει τον στόχο μας: δυστυχώς η επιθυμητή ανισότητα ΔΕΝ ισχύει στο δοθέν διάστημα, πχ για

ή για
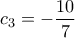
(όπου η

έχει ολικό ελάχιστο στο
![[-2,0] [-2,0]](/forum/ext/geomar/texintegr/latexrender/pictures/5743178200081e6d6488c773516b1c6f.png)
).
![P(x) \in \mathbb{R}[x] P(x) \in \mathbb{R}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/494c0a17a0894cf082818401fa40c9c4.png) με μη μηδενικό σταθερό όρο. Θα λέμε ότι το πολυώνυμο είναι
με μη μηδενικό σταθερό όρο. Θα λέμε ότι το πολυώνυμο είναι  αν και μόνο αν οι ρίζες του είναι ακριβώς οι μη μεγιστοβάθμιοι συντελεστές του (με τις σωστές πολλαπλότητες), δηλαδή
αν και μόνο αν οι ρίζες του είναι ακριβώς οι μη μεγιστοβάθμιοι συντελεστές του (με τις σωστές πολλαπλότητες), δηλαδή με
με  .
. πολυώνυμα στο
πολυώνυμα στο ![\mathbb{Q}[x] \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/59c97504827af854ac13187c78ef7320.png) .
. πολυώνυμο βαθμού
πολυώνυμο βαθμού  .
.
 προκύπτουν οι
προκύπτουν οι  ,
,  ,
,  .
.  προκύπτει άμεσα η
προκύπτει άμεσα η 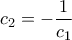 ,
,  , οδηγεί στην
, οδηγεί στην  .
.  ,
,  . Συμπεραίνουμε, με
. Συμπεραίνουμε, με 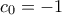 ,
,  , ότι το μοναδικό τριτοβάθμιο πολυώνυμο με την ζητούμενη ιδιότητα και με ρητούς συντελεστές είναι το
, ότι το μοναδικό τριτοβάθμιο πολυώνυμο με την ζητούμενη ιδιότητα και με ρητούς συντελεστές είναι το  .
. , που είναι η
, που είναι η  , οπότε από τους παραπάνω τύπους προκύπτουν οι
, οπότε από τους παραπάνω τύπους προκύπτουν οι  ,
,  , και το ζητούμενο πολυώνυμο είναι, προσεγγιστικά πάντοτε, το
, και το ζητούμενο πολυώνυμο είναι, προσεγγιστικά πάντοτε, το  .
.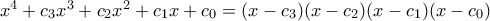 προκύπτουν, όπως και στην περίπτωση του τριτοβάθμιου πολυωνύμου, οι σχέσεις
προκύπτουν, όπως και στην περίπτωση του τριτοβάθμιου πολυωνύμου, οι σχέσεις και
και  ,
,


 , και μία προσεγγιστική, την
, και μία προσεγγιστική, την  ,
,  . Η πρώτη λύση απορρίπτεται γιατί οδηγεί στην
. Η πρώτη λύση απορρίπτεται γιατί οδηγεί στην 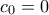 , ενώ η δεύτερη μας δίνει, προσεγγιστικά πάντοτε, το μοναδικό SNS πολυώνυμο τετάρτου βαθμού, το
, ενώ η δεύτερη μας δίνει, προσεγγιστικά πάντοτε, το μοναδικό SNS πολυώνυμο τετάρτου βαθμού, το
 ,
,  ,
,  ,
,  .)
.) : δεν υπάρχει προφανής λόγος γι αυτό, σύμπτωση δεν μπορεί να είναι, ίσως να κρύβει κάποια μεγάλη αλήθεια;
: δεν υπάρχει προφανής λόγος γι αυτό, σύμπτωση δεν μπορεί να είναι, ίσως να κρύβει κάποια μεγάλη αλήθεια;




 είτε ως δευτεροβάθμια ως προς
είτε ως δευτεροβάθμια ως προς  , συμπεραίνουμε ότι έχει πραγματικές λύσεις ως προς
, συμπεραίνουμε ότι έχει πραγματικές λύσεις ως προς  ,
,  ,
, 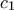 αν και μόνον αν είναι μη αρνητικές οι αντίστοιχες διακρίνουσες, δηλαδή αν και μόνον αν ισχύουν ταυτόχρονα οι ανισότητες
αν και μόνον αν είναι μη αρνητικές οι αντίστοιχες διακρίνουσες, δηλαδή αν και μόνον αν ισχύουν ταυτόχρονα οι ανισότητες 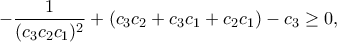

 , συνεπαγόμενη τις
, συνεπαγόμενη τις  ,
,  ,
,  . Ισχύοντας λοιπόν η δεύτερη ανισότητα διακρίνουσας ... δημιουργεί ελπίδες μη ισχύος της πρώτης ανισότητας διακρίνουσας ... καθώς οι μικρές σχετικά τιμές των
. Ισχύοντας λοιπόν η δεύτερη ανισότητα διακρίνουσας ... δημιουργεί ελπίδες μη ισχύος της πρώτης ανισότητας διακρίνουσας ... καθώς οι μικρές σχετικά τιμές των  , κλπ κλπ
, κλπ κλπ και
και  , καθώς και την δεύτερη ανισότητα διακρίνουσας στις μορφές
, καθώς και την δεύτερη ανισότητα διακρίνουσας στις μορφές  και
και  , συμπεραίνουμε ότι ισχύει η ανισότητα
, συμπεραίνουμε ότι ισχύει η ανισότητα 
 , ισοδύναμη προς την
, ισοδύναμη προς την  για
για  ή για
ή για 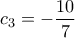 (όπου η
(όπου η  έχει ολικό ελάχιστο στο
έχει ολικό ελάχιστο στο ![[-2,0] [-2,0]](/forum/ext/geomar/texintegr/latexrender/pictures/5743178200081e6d6488c773516b1c6f.png) ).
).

 ,
,  ,
,  , οι οποίες, σε συνδυασμό με τις γνωστές (ΑΓΜ) ανισότητες
, οι οποίες, σε συνδυασμό με τις γνωστές (ΑΓΜ) ανισότητες  και
και  , δίνουν για την πρώτη διακρίνουσα
, δίνουν για την πρώτη διακρίνουσα

 ) της ανισότητας που αποδείχθηκε
) της ανισότητας που αποδείχθηκε  ,
,  , κλπ
, κλπ . Άρα
. Άρα  ,
,  και
και  .
. 
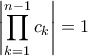 . Μαζί με τα παραπάνω, αυτό συνεπάγεται ότι
. Μαζί με τα παραπάνω, αυτό συνεπάγεται ότι 

 .
. , οπότε φτάνουμε στο άτοπο.
, οπότε φτάνουμε στο άτοπο.
 και
και  , και υπάρχουν και άλλες ομοιότητες. Η κύρια διαφορά είναι ότι εγώ καταφεύγω, γενικότερα, στην ανυπαρξία πραγματικών λύσεων της
, και υπάρχουν και άλλες ομοιότητες. Η κύρια διαφορά είναι ότι εγώ καταφεύγω, γενικότερα, στην ανυπαρξία πραγματικών λύσεων της
 (σίγουρα) και για
(σίγουρα) και για  (σχεδόν σίγουρα).
(σχεδόν σίγουρα).