 πραγματικοί αριθμοί. Ονομάζουμε
πραγματικοί αριθμοί. Ονομάζουμε  το σύνολο των σημείων
το σύνολο των σημείων  του Ευκλείδειου χώρου για τα οποία
του Ευκλείδειου χώρου για τα οποία  . Έστω επίσης πραγματικοί αριθμοί
. Έστω επίσης πραγματικοί αριθμοί  τέτοιοι ώστε
τέτοιοι ώστε  για κάθε
για κάθε  .
.Να αποδειχθεί ότι υπάρχει πραγματικός αριθμός
![t \in [0,1] t \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/dff6e05ec00b53d46e366975136d0d2e.png) τέτοιος ώστε
τέτοιος ώστε 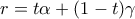 και
και  .
. πραγματικοί αριθμοί. Ονομάζουμε
πραγματικοί αριθμοί. Ονομάζουμε  το σύνολο των σημείων
το σύνολο των σημείων  του Ευκλείδειου χώρου για τα οποία
του Ευκλείδειου χώρου για τα οποία  . Έστω επίσης πραγματικοί αριθμοί
. Έστω επίσης πραγματικοί αριθμοί  τέτοιοι ώστε
τέτοιοι ώστε  για κάθε
για κάθε  .
.![t \in [0,1] t \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/dff6e05ec00b53d46e366975136d0d2e.png) τέτοιος ώστε
τέτοιος ώστε 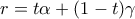 και
και  .
. είναι το εσωτερικό του 'αντίσκηνου' που ορίζουν τα επίπεδα
είναι το εσωτερικό του 'αντίσκηνου' που ορίζουν τα επίπεδα 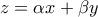 και
και  ... καθώς ισχύουν οι ανισότητες
... καθώς ισχύουν οι ανισότητες  και
και  , ενώ το τρίτο επίπεδο,
, ενώ το τρίτο επίπεδο,  , είναι το 'σκέπαστρο' ... καθώς ισχύει η
, είναι το 'σκέπαστρο' ... καθώς ισχύει η  για όλα τα σημεία
για όλα τα σημεία  του
του  .
. 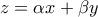 και
και  ), κάτι που δεν προκύπτει από την λεγόμενη 'κοινή λογική' αλλά από την ψυχρή λογική των (αν)ισοτήτων:
), κάτι που δεν προκύπτει από την λεγόμενη 'κοινή λογική' αλλά από την ψυχρή λογική των (αν)ισοτήτων: 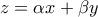 και
και  είναι η
είναι η  ,
,  . Θέτοντας
. Θέτοντας  ,
, 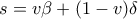 (με
(με  ,
,  προσδιοριζόμενους από τους
προσδιοριζόμενους από τους  ,
,  ,
,  και τους
και τους  ,
,  ,
, 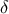 , αντίστοιχα), αλλά και
, αντίστοιχα), αλλά και  ,
,  , στην
, στην  (που οφείλει να ισχύει για κάθε σημείο του
(που οφείλει να ισχύει για κάθε σημείο του  , άρα και για την τομή των δύο επιπέδων), καταλήγουμε στην ανισότητα
, άρα και για την τομή των δύο επιπέδων), καταλήγουμε στην ανισότητα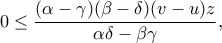
 αν και μόνον αν
αν και μόνον αν  (όπου
(όπου  κάποιος πραγματικός): προκύπτει εύκολα τώρα ότι οι
κάποιος πραγματικός): προκύπτει εύκολα τώρα ότι οι  ,
,  ικανοποιούν την
ικανοποιούν την  , όπου πλέον
, όπου πλέον  ,
,  .
.  . Αυτό προκύπτει εύκολα από γεωμετρική θεώρηση (του αντίσκηνου και του σκέπαστρου): ένα επίπεδο ('σκέπαστρο' με εξίσωση
. Αυτό προκύπτει εύκολα από γεωμετρική θεώρηση (του αντίσκηνου και του σκέπαστρου): ένα επίπεδο ('σκέπαστρο' με εξίσωση  ) διερχόμενο από την τομή δύο άλλων επιπέδων (
) διερχόμενο από την τομή δύο άλλων επιπέδων (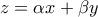 ,
,  ) βρίσκεται 'πάνω' από την τομή των δύο επιπέδων ('καλύπτει δηλαδή το 'εσωτερικό' των δύο επιπέδων 'αντίσκηνο'
) βρίσκεται 'πάνω' από την τομή των δύο επιπέδων ('καλύπτει δηλαδή το 'εσωτερικό' των δύο επιπέδων 'αντίσκηνο'  , καθώς
, καθώς  για
για  ) ... αν και μόνον αν το κάθετο του επίπεδο
) ... αν και μόνον αν το κάθετο του επίπεδο  είναι 'εσωτερικό' των καθέτων διανυσμάτων
είναι 'εσωτερικό' των καθέτων διανυσμάτων  ,
,  των δύο επιπέδων, δηλαδή αν και μόνον αν
των δύο επιπέδων, δηλαδή αν και μόνον αν  με
με  , κάτι που όντως ισχύει, για
, κάτι που όντως ισχύει, για 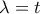 , λόγω των
, λόγω των  ,
,  . Άρα
. Άρα  . (Γίνεται και χωρίς χρήση διανυσμάτων...)
. (Γίνεται και χωρίς χρήση διανυσμάτων...)  : αν
: αν  τότε
τότε  (τομή),
(τομή),  και
και ![t\in [0,1] t\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d9a06fde4663cdd5b1ba693e9127232f.png) , αν
, αν 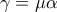 ,
,  , τότε
, τότε  (τομή),
(τομή),  ,
, 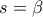 και
και  .]
.] .
. καθώς και
καθώς και  . Άρα
. Άρα  και ομοίως
και ομοίως  . Μπορούμε να διαλέξουμε οποιοδήποτε
. Μπορούμε να διαλέξουμε οποιοδήποτε ![t \in [0,1] t \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/dff6e05ec00b53d46e366975136d0d2e.png) .
.  .
.  .
.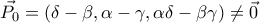 και το
και το  (όπου
(όπου  παράμετρος). Ισχύει
παράμετρος). Ισχύει 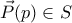 , οπότε
, οπότε ![p \left[ r(\delta - \beta) + s(\alpha - \gamma) - (\alpha \delta - \beta \gamma) \right] \geqslant 0 p \left[ r(\delta - \beta) + s(\alpha - \gamma) - (\alpha \delta - \beta \gamma) \right] \geqslant 0](/forum/ext/geomar/texintegr/latexrender/pictures/feb8582ca1cca7926a3cf6499922a62a.png) για κάθε
για κάθε  . Έτσι,
. Έτσι,  .
. γραμμικώς ανεξάρτητα, πρέπει να ισχύει
γραμμικώς ανεξάρτητα, πρέπει να ισχύει  . Aπό την συντεταγμένη
. Aπό την συντεταγμένη  παίρνουμε
παίρνουμε  .
. (ομοίως σε άλλη περίπτωση). Ισχύει
(ομοίως σε άλλη περίπτωση). Ισχύει  καθώς και
καθώς και  . Έτσι,
. Έτσι, ![t \in [0,1] t \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/dff6e05ec00b53d46e366975136d0d2e.png) .
.

 (1)
(1)


 η (1) γίνεται
η (1) γίνεται 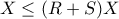

 η (1) δίνει
η (1) δίνει 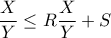
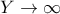 παίρνουμε
παίρνουμε 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες