Μια προσπάθεια, αλλά δεν είμαι σίγουρος...

- sns_2017_p5.png (15.04 KiB) Προβλήθηκε 1596 φορές
Έστω ότι το μυρμήγκι περπατάει από το σημείο

σε ένα σημείο

της περιφέρειας του εξωτερικού κύκλου του δακτυλίου το οποίο ύστερα από κατάλληλη περιστροφή θα συμπέσει με το

ώστε να φτάσει στον προορισμό του. Αν το σημείο

βρίσκεται στο δεξί ημιεπίπεδο που ορίζει η κάθετη προς την

στο

, τότε η ελάχιστη απόσταση που χρειάζεται να περπατήσει είναι ίση με το ευθύγραμμο τμήμα που ορίζουν αυτά τα σημεία, δηλαδή

. Σε αυτό το τμήμα θα αντιστοιχεί και ο ελάχιστος χρόνος για να φτάσει εκεί, αρκεί να υπάρχει και το κατάλληλο

.
Ας υπολογίσουμε αρχικά το

συναρτήση της γωνίας

, με θετικές τιμές προς την φορά των δεικτών του ρολογιού αντίθετα δηλαδή προς την κίνηση της πλατφόρμας. Είναι

. Από το θεώρημα διαμέσων έχουμε


(1)
Αφού το μερμύγκι έχει μοναδιαία ταχύτητα θα χρειαστεί χρόνο

(μονάδες χρόνου) για να φτάσει στο

. Για να φτάσει το

στο

πρέπει η πλατφόρμα να περιστραφεί κατά γωνία

και αφού κάνει

περιστροφές στη μονάδα του χρόνου θα χρειαστεί χρόνο

. Αν υπάρχει

ώστε

, τότε το μυρμήγκι θα φτάσει στο

στον ελάχιστο χρόνο, αφού έτσι θα περπατήσει μόνο ευθεία.
Δηλαδή ισχύει

(2) (Η σχέση που έβγαλε ο κ.Ρεκούμης παραπάνω)
Θεωρούμε τώρα την συνάρτηση
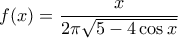
η οποία είναι συνεχής και στα άκρα του διάστηματος
![[0, \dfrac{\pi}{3}] [0, \dfrac{\pi}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/0432daf94a83c6685d30c05705d349f9.png)
παίρνει τιμές

,

. Ως συνεχής
![\forall w \in [0,\sqrt{3}/18] \forall w \in [0,\sqrt{3}/18]](/forum/ext/geomar/texintegr/latexrender/pictures/0d47b27b45b12a7950cd690e618640ed.png)
υπάρχει τουλάχιστον ένα

για το οποίο

. Θα δείξουμε ότι η συνάρτηση

είναι γνησίως αύξουσα στο διάστημα
![[0, \pi/3] [0, \pi/3]](/forum/ext/geomar/texintegr/latexrender/pictures/cbebbd4a8416442ed920cb1438a50632.png)
, οπότε θα είναι και μοναδικό. Πράγματι έχουμε
![f'(x) = \dfrac{5-4\cos x -2x \sin x}{2\pi \sqrt[3]{(5-4\cos x)^2}} f'(x) = \dfrac{5-4\cos x -2x \sin x}{2\pi \sqrt[3]{(5-4\cos x)^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/5f2ed34d368a2fa05dc5331a1858fafc.png)
. Αρκεί δηλαδή ο παρονομαστής να είναι θετικός.
a) Για

έχουμε


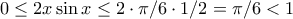
και αφού

, θα είναι

.
b) Για
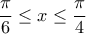
έχουμε


. Οπότε

.
c) Για

έχουμε


. Οπότε

. Άρα και σε αυτή την περίπτωση η παράγωγος είναι θετική.
Αφού η

είναι γνησίως αύξουσα στο παραπάνω διάστημα θα αντιστρέφεται. Ας είναι

η αντίστροφής της η οποία ορίζεται στο διάστημα
![w \in [ f(0)=0, f(\pi /3) = \sqrt{3}/18]=[0,\dfrac{\sqrt{3}}{18}] w \in [ f(0)=0, f(\pi /3) = \sqrt{3}/18]=[0,\dfrac{\sqrt{3}}{18}]](/forum/ext/geomar/texintegr/latexrender/pictures/4f2debc861bdc6524a2e01c32c972503.png)
. Δηλαδή είναι
![f^{-1}_{1}(w) : [0,\dfrac{\sqrt{3}}{18}] \rightarrow [0, \dfrac{\pi}{3}] f^{-1}_{1}(w) : [0,\dfrac{\sqrt{3}}{18}] \rightarrow [0, \dfrac{\pi}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/2d624dbceb4b328522a8f1ff1bb3284a.png)
με
![f_{1}(x)=f(x), x \in [ 0, \dfrac{\pi}{3}] f_{1}(x)=f(x), x \in [ 0, \dfrac{\pi}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/d3c3aea214433f3fd73be4eed025375a.png) (i)
(i)
To δε ελάχιστο

θα είναι

,
![w \in [0,\dfrac{\sqrt{3}}{18}] w \in [0,\dfrac{\sqrt{3}}{18}]](/forum/ext/geomar/texintegr/latexrender/pictures/997477a033a1c0a6e6bb0510341ac95d.png)
Ομοίως εργαζόμαστε και για γωνίες
![x \in [\dfrac{5\pi}{3}, 2\pi] x \in [\dfrac{5\pi}{3}, 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/fbba24733759aeeb3562139af1fce8d0.png)
για τις οποίες πάλι η

είναι γνησιώς αύξουσα. Ας αν είναι

η αντίστροφής της η οποία ορίζεται στο διάστημα
![w \in [ f(\dfrac{5\pi}{3})=\dfrac{\sqrt{3}}{6}, f(2 \pi) = 1]=[\dfrac{\sqrt{3}}{6},1] w \in [ f(\dfrac{5\pi}{3})=\dfrac{\sqrt{3}}{6}, f(2 \pi) = 1]=[\dfrac{\sqrt{3}}{6},1]](/forum/ext/geomar/texintegr/latexrender/pictures/8858078f304aa3131a3a5dca78403238.png)
. Δηλαδή
![f^{-1}_{2}(w) : [\dfrac{\sqrt{3}}{6},1] \rightarrow [\dfrac{5\pi}{3}, 2\pi] f^{-1}_{2}(w) : [\dfrac{\sqrt{3}}{6},1] \rightarrow [\dfrac{5\pi}{3}, 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/eb884c19b03f78ac2069f14ff7cc0a95.png)
με
![f_{2}(x)=f(x), x \in [\dfrac{5\pi}{3}, 2\pi] f_{2}(x)=f(x), x \in [\dfrac{5\pi}{3}, 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/c3c2bd189362a9aff8220c0538b1c01a.png) (ii)
(ii)
Αν τώρα το σημείο

(

στο σχήμα) αντιστοιχεί σε γωνίες
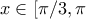
] έχουμε:
Έστω το μυρμήγκι ακολουθεί μια διαδρομή, τυχαία καμπύλη,

. Ας είναι

σημείο του εσωτερικού κύκλου ώστε
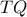
εφαπτομένη του. Τα σημεία

βρίσκονται εκατέροθεν αυτής, οπότε η καμπύλη

θα την τέμνει σε κάπιο σημείο, έστω

που θα βρίσκεται στην ημιευθεία με άκρη το

που δεν περιέχει το

.
Τότε θα είναι (με δείκτη

είναι οι καμπύλες αλλιώς το ευθύγραμμο τμήμα).

(όπου

το τόξο του εσωτερικού κύκλου). Αφού η ελάχιστη διαδρομή που εννώνει δυο σημεία του εσωτερικού κύκλου είναι το αντίστοιχο ελάχιστο τόξο, σύμφωνα με την εκφώνηση.
Δηλαδή η ελάχιστη διαδρομή για το σημείο

είναι η εφαπτομένη
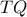
συν το τόξο

. Από δύναμη σημείου προς κύκλο βρίσκουμε ότι

. Οπότε το μήκος του τόξου

θα είναι
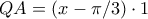
και όλη η διαδρομή για το

.

. Όπως και παραπάνω θα πρέπει
 (3)
(3)
Ορίζουμε μια νέα συνάρτηση
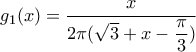
![x \in [\dfrac{\pi}{3},\pi] x \in [\dfrac{\pi}{3},\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/d14b91206723466eb910f486e2637c92.png)
.
Είναι
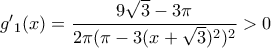
. Οπότε η

αντιστρέφεται σε αυτό διάστημα με
![w \in [g_{1}(\dfrac{\pi}{3}), g_{1}(\pi)] = [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}] w \in [g_{1}(\dfrac{\pi}{3}), g_{1}(\pi)] = [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}]](/forum/ext/geomar/texintegr/latexrender/pictures/8b1d38614b0c36227a025470610b24c0.png)
Λύνοντας την (3) ως προς

βρίσκουμε για την αντίστροφή της
 (iii)
(iii)
Ο δε ελάχιστος χρόνος

θα είναι

με
![w \in [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}] w \in [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}]](/forum/ext/geomar/texintegr/latexrender/pictures/bbc6e955ccb6e58591b8387988947a59.png)
Στην συνέχεια εργαζόμαστε για τις συμμετρικές διαδρομές, για
που βρίσκονται στο πάνω ημικύκλιο. Σε αυτή την περίπτωση παρόμοια με παραπάνω θα είναι

,
![x \in [\pi, 5\pi /3] x \in [\pi, 5\pi /3]](/forum/ext/geomar/texintegr/latexrender/pictures/d25e9d0a46432d1254c8e34a9a7a1781.png) (4)
(4)
Λύνοντας την (3) ως προς

βρίσκουμε για την αντίστροφή της
 (iv)
(iv)
Ο δε ελάχιστος χρόνος

θα είναι

με
![w \in [\dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6}] w \in [\dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6}]](/forum/ext/geomar/texintegr/latexrender/pictures/b3df1d71e41f1f83d9f456042d64bb3d.png)
Συνοψίζοντας τα
(i), (ii), (iii), (iv) βρίσκουμε για το

![\Displaystyle{T(w) = \left\{\begin{matrix}
\sqrt{5-4\cos (f^{-1}_{1}(w))} , w \in \left [ 0,\dfrac{\sqrt{3}}{18} \right )\\
\sqrt{3} + \dfrac{2\pi(\sqrt{3}-\pi/3)w}{1-2\pi w} -\pi/3 , w \in\left [ \dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})} \right ) \\
\sqrt{3} + 5\pi/3-\dfrac{2\pi(\sqrt{3}+5\pi/3)w}{1+2\pi w}, w \in \left [ \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6} \right )\\
\sqrt{5-4\cos (f^{-1}_{2}(w))} , w \in \left [ \dfrac{\sqrt{3}}{6},1 \right ]
\end{matrix}\right.} \Displaystyle{T(w) = \left\{\begin{matrix}
\sqrt{5-4\cos (f^{-1}_{1}(w))} , w \in \left [ 0,\dfrac{\sqrt{3}}{18} \right )\\
\sqrt{3} + \dfrac{2\pi(\sqrt{3}-\pi/3)w}{1-2\pi w} -\pi/3 , w \in\left [ \dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})} \right ) \\
\sqrt{3} + 5\pi/3-\dfrac{2\pi(\sqrt{3}+5\pi/3)w}{1+2\pi w}, w \in \left [ \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6} \right )\\
\sqrt{5-4\cos (f^{-1}_{2}(w))} , w \in \left [ \dfrac{\sqrt{3}}{6},1 \right ]
\end{matrix}\right.}](/forum/ext/geomar/texintegr/latexrender/pictures/a1f267dbc12588ba3cee0871c68863d2.png) Edit: ( 22/11/17) Έγιναν μερικές τροποποιήσεις στην αρχική ανάρτηση σύμφωνα με τις παρατηρήσεις στο παρακάτω ποστ.
Edit: ( 22/11/17) Έγιναν μερικές τροποποιήσεις στην αρχική ανάρτηση σύμφωνα με τις παρατηρήσεις στο παρακάτω ποστ.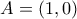 και θέλοντας να φτάσει στο σημείο
και θέλοντας να φτάσει στο σημείο  . Είναι όμως αναγκασμένο να περπατάει σε μία πλατφόρμα με μορφή δακτυλίου με κέντρο το
. Είναι όμως αναγκασμένο να περπατάει σε μία πλατφόρμα με μορφή δακτυλίου με κέντρο το  και ακτίνες
και ακτίνες  (εσωτερική) και
(εσωτερική) και  (εξωτερική). Σε σχέση με την πλατφόρμα, μπορεί να κινείται με μοναδιαία ταχύτητα προς οποιαδήποτε κατεύθυνση. Η πλατφόρμα περιστρέφεται με φορά αντίθετη των δεικτών του ρολογιού με σταθερή ταχύτητα, εκτελώντας
(εξωτερική). Σε σχέση με την πλατφόρμα, μπορεί να κινείται με μοναδιαία ταχύτητα προς οποιαδήποτε κατεύθυνση. Η πλατφόρμα περιστρέφεται με φορά αντίθετη των δεικτών του ρολογιού με σταθερή ταχύτητα, εκτελώντας  στροφές ανά μονάδα χρόνου, με
στροφές ανά μονάδα χρόνου, με  . Ποιος είναι ο ελάχιστος χρόνος
. Ποιος είναι ο ελάχιστος χρόνος  , συναρτήσει του
, συναρτήσει του  , που χρειάζεται για να φτάσει στο
, που χρειάζεται για να φτάσει στο  ;
; 
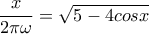 με
με  ;
; σε ένα σημείο
σε ένα σημείο  της περιφέρειας του εξωτερικού κύκλου του δακτυλίου το οποίο ύστερα από κατάλληλη περιστροφή θα συμπέσει με το
της περιφέρειας του εξωτερικού κύκλου του δακτυλίου το οποίο ύστερα από κατάλληλη περιστροφή θα συμπέσει με το  στο
στο  . Σε αυτό το τμήμα θα αντιστοιχεί και ο ελάχιστος χρόνος για να φτάσει εκεί, αρκεί να υπάρχει και το κατάλληλο
. Σε αυτό το τμήμα θα αντιστοιχεί και ο ελάχιστος χρόνος για να φτάσει εκεί, αρκεί να υπάρχει και το κατάλληλο  .
. , με θετικές τιμές προς την φορά των δεικτών του ρολογιού αντίθετα δηλαδή προς την κίνηση της πλατφόρμας. Είναι
, με θετικές τιμές προς την φορά των δεικτών του ρολογιού αντίθετα δηλαδή προς την κίνηση της πλατφόρμας. Είναι  . Από το θεώρημα διαμέσων έχουμε
. Από το θεώρημα διαμέσων έχουμε 
 (1)
(1) και αφού κάνει
και αφού κάνει  . Αν υπάρχει
. Αν υπάρχει  , τότε το μυρμήγκι θα φτάσει στο
, τότε το μυρμήγκι θα φτάσει στο  (2) (Η σχέση που έβγαλε ο κ.Ρεκούμης παραπάνω)
(2) (Η σχέση που έβγαλε ο κ.Ρεκούμης παραπάνω)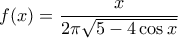 η οποία είναι συνεχής και στα άκρα του διάστηματος
η οποία είναι συνεχής και στα άκρα του διάστηματος ![[0, \dfrac{\pi}{3}] [0, \dfrac{\pi}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/0432daf94a83c6685d30c05705d349f9.png) παίρνει τιμές
παίρνει τιμές  ,
,  . Ως συνεχής
. Ως συνεχής ![\forall w \in [0,\sqrt{3}/18] \forall w \in [0,\sqrt{3}/18]](/forum/ext/geomar/texintegr/latexrender/pictures/0d47b27b45b12a7950cd690e618640ed.png) υπάρχει τουλάχιστον ένα
υπάρχει τουλάχιστον ένα  για το οποίο
για το οποίο  . Θα δείξουμε ότι η συνάρτηση
. Θα δείξουμε ότι η συνάρτηση  είναι γνησίως αύξουσα στο διάστημα
είναι γνησίως αύξουσα στο διάστημα ![[0, \pi/3] [0, \pi/3]](/forum/ext/geomar/texintegr/latexrender/pictures/cbebbd4a8416442ed920cb1438a50632.png) , οπότε θα είναι και μοναδικό. Πράγματι έχουμε
, οπότε θα είναι και μοναδικό. Πράγματι έχουμε![f'(x) = \dfrac{5-4\cos x -2x \sin x}{2\pi \sqrt[3]{(5-4\cos x)^2}} f'(x) = \dfrac{5-4\cos x -2x \sin x}{2\pi \sqrt[3]{(5-4\cos x)^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/5f2ed34d368a2fa05dc5331a1858fafc.png) . Αρκεί δηλαδή ο παρονομαστής να είναι θετικός.
. Αρκεί δηλαδή ο παρονομαστής να είναι θετικός. έχουμε
έχουμε 

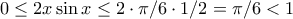 και αφού
και αφού  , θα είναι
, θα είναι  .
.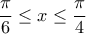 έχουμε
έχουμε 
 . Οπότε
. Οπότε  .
. έχουμε
έχουμε 
 . Οπότε
. Οπότε  . Άρα και σε αυτή την περίπτωση η παράγωγος είναι θετική.
. Άρα και σε αυτή την περίπτωση η παράγωγος είναι θετική. είναι γνησίως αύξουσα στο παραπάνω διάστημα θα αντιστρέφεται. Ας είναι
είναι γνησίως αύξουσα στο παραπάνω διάστημα θα αντιστρέφεται. Ας είναι  η αντίστροφής της η οποία ορίζεται στο διάστημα
η αντίστροφής της η οποία ορίζεται στο διάστημα ![w \in [ f(0)=0, f(\pi /3) = \sqrt{3}/18]=[0,\dfrac{\sqrt{3}}{18}] w \in [ f(0)=0, f(\pi /3) = \sqrt{3}/18]=[0,\dfrac{\sqrt{3}}{18}]](/forum/ext/geomar/texintegr/latexrender/pictures/4f2debc861bdc6524a2e01c32c972503.png) . Δηλαδή είναι
. Δηλαδή είναι![f^{-1}_{1}(w) : [0,\dfrac{\sqrt{3}}{18}] \rightarrow [0, \dfrac{\pi}{3}] f^{-1}_{1}(w) : [0,\dfrac{\sqrt{3}}{18}] \rightarrow [0, \dfrac{\pi}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/2d624dbceb4b328522a8f1ff1bb3284a.png) με
με ![f_{1}(x)=f(x), x \in [ 0, \dfrac{\pi}{3}] f_{1}(x)=f(x), x \in [ 0, \dfrac{\pi}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/d3c3aea214433f3fd73be4eed025375a.png) (i)
(i) θα είναι
θα είναι  ,
, ![w \in [0,\dfrac{\sqrt{3}}{18}] w \in [0,\dfrac{\sqrt{3}}{18}]](/forum/ext/geomar/texintegr/latexrender/pictures/997477a033a1c0a6e6bb0510341ac95d.png)
![x \in [\dfrac{5\pi}{3}, 2\pi] x \in [\dfrac{5\pi}{3}, 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/fbba24733759aeeb3562139af1fce8d0.png) για τις οποίες πάλι η
για τις οποίες πάλι η  η αντίστροφής της η οποία ορίζεται στο διάστημα
η αντίστροφής της η οποία ορίζεται στο διάστημα ![w \in [ f(\dfrac{5\pi}{3})=\dfrac{\sqrt{3}}{6}, f(2 \pi) = 1]=[\dfrac{\sqrt{3}}{6},1] w \in [ f(\dfrac{5\pi}{3})=\dfrac{\sqrt{3}}{6}, f(2 \pi) = 1]=[\dfrac{\sqrt{3}}{6},1]](/forum/ext/geomar/texintegr/latexrender/pictures/8858078f304aa3131a3a5dca78403238.png) . Δηλαδή
. Δηλαδή![f^{-1}_{2}(w) : [\dfrac{\sqrt{3}}{6},1] \rightarrow [\dfrac{5\pi}{3}, 2\pi] f^{-1}_{2}(w) : [\dfrac{\sqrt{3}}{6},1] \rightarrow [\dfrac{5\pi}{3}, 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/eb884c19b03f78ac2069f14ff7cc0a95.png) με
με ![f_{2}(x)=f(x), x \in [\dfrac{5\pi}{3}, 2\pi] f_{2}(x)=f(x), x \in [\dfrac{5\pi}{3}, 2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/c3c2bd189362a9aff8220c0538b1c01a.png) (ii)
(ii) στο σχήμα) αντιστοιχεί σε γωνίες
στο σχήμα) αντιστοιχεί σε γωνίες 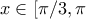 ] έχουμε:
] έχουμε: . Ας είναι
. Ας είναι  σημείο του εσωτερικού κύκλου ώστε
σημείο του εσωτερικού κύκλου ώστε 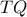 εφαπτομένη του. Τα σημεία
εφαπτομένη του. Τα σημεία  βρίσκονται εκατέροθεν αυτής, οπότε η καμπύλη
βρίσκονται εκατέροθεν αυτής, οπότε η καμπύλη  που θα βρίσκεται στην ημιευθεία με άκρη το
που θα βρίσκεται στην ημιευθεία με άκρη το  είναι οι καμπύλες αλλιώς το ευθύγραμμο τμήμα).
είναι οι καμπύλες αλλιώς το ευθύγραμμο τμήμα). (όπου
(όπου  το τόξο του εσωτερικού κύκλου). Αφού η ελάχιστη διαδρομή που εννώνει δυο σημεία του εσωτερικού κύκλου είναι το αντίστοιχο ελάχιστο τόξο, σύμφωνα με την εκφώνηση.
το τόξο του εσωτερικού κύκλου). Αφού η ελάχιστη διαδρομή που εννώνει δυο σημεία του εσωτερικού κύκλου είναι το αντίστοιχο ελάχιστο τόξο, σύμφωνα με την εκφώνηση. . Οπότε το μήκος του τόξου
. Οπότε το μήκος του τόξου 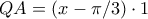 και όλη η διαδρομή για το
και όλη η διαδρομή για το  . Όπως και παραπάνω θα πρέπει
. Όπως και παραπάνω θα πρέπει  (3)
(3)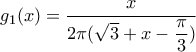
![x \in [\dfrac{\pi}{3},\pi] x \in [\dfrac{\pi}{3},\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/d14b91206723466eb910f486e2637c92.png) .
.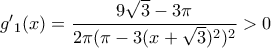 . Οπότε η
. Οπότε η  αντιστρέφεται σε αυτό διάστημα με
αντιστρέφεται σε αυτό διάστημα με ![w \in [g_{1}(\dfrac{\pi}{3}), g_{1}(\pi)] = [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}] w \in [g_{1}(\dfrac{\pi}{3}), g_{1}(\pi)] = [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}]](/forum/ext/geomar/texintegr/latexrender/pictures/8b1d38614b0c36227a025470610b24c0.png)
 (iii)
(iii) με
με ![w \in [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}] w \in [\dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}]](/forum/ext/geomar/texintegr/latexrender/pictures/bbc6e955ccb6e58591b8387988947a59.png)
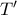 που βρίσκονται στο πάνω ημικύκλιο. Σε αυτή την περίπτωση παρόμοια με παραπάνω θα είναι
που βρίσκονται στο πάνω ημικύκλιο. Σε αυτή την περίπτωση παρόμοια με παραπάνω θα είναι ,
, ![x \in [\pi, 5\pi /3] x \in [\pi, 5\pi /3]](/forum/ext/geomar/texintegr/latexrender/pictures/d25e9d0a46432d1254c8e34a9a7a1781.png) (4)
(4)  (iv)
(iv) με
με ![w \in [\dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6}] w \in [\dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6}]](/forum/ext/geomar/texintegr/latexrender/pictures/b3df1d71e41f1f83d9f456042d64bb3d.png)
![\Displaystyle{T(w) = \left\{\begin{matrix}
\sqrt{5-4\cos (f^{-1}_{1}(w))} , w \in \left [ 0,\dfrac{\sqrt{3}}{18} \right )\\
\sqrt{3} + \dfrac{2\pi(\sqrt{3}-\pi/3)w}{1-2\pi w} -\pi/3 , w \in\left [ \dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})} \right ) \\
\sqrt{3} + 5\pi/3-\dfrac{2\pi(\sqrt{3}+5\pi/3)w}{1+2\pi w}, w \in \left [ \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6} \right )\\
\sqrt{5-4\cos (f^{-1}_{2}(w))} , w \in \left [ \dfrac{\sqrt{3}}{6},1 \right ]
\end{matrix}\right.} \Displaystyle{T(w) = \left\{\begin{matrix}
\sqrt{5-4\cos (f^{-1}_{1}(w))} , w \in \left [ 0,\dfrac{\sqrt{3}}{18} \right )\\
\sqrt{3} + \dfrac{2\pi(\sqrt{3}-\pi/3)w}{1-2\pi w} -\pi/3 , w \in\left [ \dfrac{\sqrt{3}}{18}, \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})} \right ) \\
\sqrt{3} + 5\pi/3-\dfrac{2\pi(\sqrt{3}+5\pi/3)w}{1+2\pi w}, w \in \left [ \dfrac{1}{2(\sqrt{3}+\dfrac{2\pi}{3})}, \dfrac{\sqrt{3}}{6} \right )\\
\sqrt{5-4\cos (f^{-1}_{2}(w))} , w \in \left [ \dfrac{\sqrt{3}}{6},1 \right ]
\end{matrix}\right.}](/forum/ext/geomar/texintegr/latexrender/pictures/a1f267dbc12588ba3cee0871c68863d2.png)
 να είναι μοναδικό,
να είναι μοναδικό,  αλλά χρωστάω την δικαιολόγηση για ακόμη μια περίπτωση ... θα επανέρθω.
αλλά χρωστάω την δικαιολόγηση για ακόμη μια περίπτωση ... θα επανέρθω.