23. Ποιά είναι η τιμή του ορίου
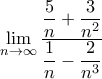 ; [2 μόρια]
; [2 μόρια]24. Αν η παραγωγίσιμη σε όλους τους πραγματικούς αριθμούς συνάρτηση
 ικανοποιεί την σχέση
ικανοποιεί την σχέση 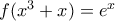 για όλους τους πραγματικούς
για όλους τους πραγματικούς  , ποιά η τιμή της
, ποιά η τιμή της 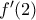 ; [3 μόρια]
; [3 μόρια]25. Ποια η τιμή του αθροίσματος
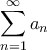 , αν
, αν 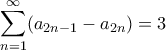 ,
, 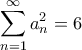 ,
, όπου
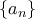 γεωμετρική πρόοδος (άπειρη); [3 μόρια]
γεωμετρική πρόοδος (άπειρη); [3 μόρια]26. Ποια η τιμή του ορίου
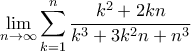 ; [3 μόρια]
; [3 μόρια]27. Το κινούμενο σημείο
 του καρτεσιανού επιπέδου την χρονική στιγμή
του καρτεσιανού επιπέδου την χρονική στιγμή 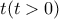 είναι το μέσο του τμήματος που ορίζουν τα δυο σημεία τομής της καμπύλης
είναι το μέσο του τμήματος που ορίζουν τα δυο σημεία τομής της καμπύλης  με την ευθεία
με την ευθεία 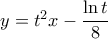 . Πόση απόσταση έχει διανύσει το σημείο
. Πόση απόσταση έχει διανύσει το σημείο  από την χρονική στιγμή
από την χρονική στιγμή  έως την χρονική στιγμή
έως την χρονική στιγμή  ; [3 μόρια]
; [3 μόρια]28. Έστω συνάρτηση
 με
με 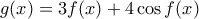 , όπου
, όπου  η συνάρτηση
η συνάρτηση 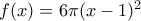 . Ποιό είναι το πλήθος των σημείων
. Ποιό είναι το πλήθος των σημείων  , με
, με 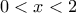 στα οποία η
στα οποία η  λαμβάνει ελάχιστη τιμή (τοπικά ελάχιστα); [4 μόρια]
λαμβάνει ελάχιστη τιμή (τοπικά ελάχιστα); [4 μόρια]29. Όπως φαίνεται στο σχήμα, δίνεται ένα ημικύκλιο διαμέτρου
 μήκους
μήκους  . Έστω
. Έστω  και
και  δυο σημεία του τόξου
δυο σημεία του τόξου  με
με 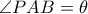 ,
, 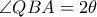 και ας είναι
και ας είναι  η τομή των τμημάτων
η τομή των τμημάτων 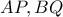 . Θεωρούμε σημείο
. Θεωρούμε σημείο  του τμήματος
του τμήματος  , σημείο
, σημείο  του τμήματος
του τμήματος 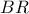 και σημείο
και σημείο  του τμήματος
του τμήματος 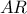 , ώστε η ευθεία
, ώστε η ευθεία 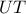 να είναι παράλληλη προς την
να είναι παράλληλη προς την  και το τρίγωνο
και το τρίγωνο 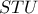 ισόπλευρο. Θεωρώντας ότι το εμβαδόν του χωρίου που περικλείεται από τα τμήματα
ισόπλευρο. Θεωρώντας ότι το εμβαδόν του χωρίου που περικλείεται από τα τμήματα 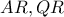 και το τόξο
και το τόξο  είναι
είναι 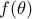 και το εμβαδόν του τριγώνου
και το εμβαδόν του τριγώνου 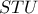 είναι
είναι 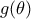 , ισχύει
, ισχύει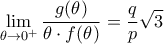 . Βρείτε την τιμή του αθροίσματος
. Βρείτε την τιμή του αθροίσματος 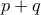 . (Όπου
. (Όπου 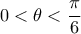 και
και  ,
, πρώτοι μεταξύ τους φυσικοί αριθμοί.) [4 μόρια]
πρώτοι μεταξύ τους φυσικοί αριθμοί.) [4 μόρια]30. Μια αύξουσα (γνησίως) και παραγωγίσιμη στο σύνολο όλων των πραγματικών αριθμών συνάρτηση
 ικανοποιεί τις ακόλουθες συνθήκες:
ικανοποιεί τις ακόλουθες συνθήκες:(Α)
 ,
, 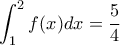
(Β) Αν
 η αντίστροφη της
η αντίστροφη της  , για όλους τους πραγματικούς
, για όλους τους πραγματικούς  με
με  είναι
είναι 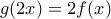
Αν
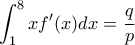 , βρείτε την τιμή του αθροίσματος
, βρείτε την τιμή του αθροίσματος 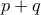 . (όπου
. (όπου  πρώτοι μεταξύ τους φυσικοί αριθμοί.) [4 μόρια]
πρώτοι μεταξύ τους φυσικοί αριθμοί.) [4 μόρια]
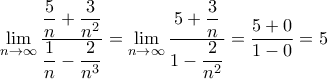
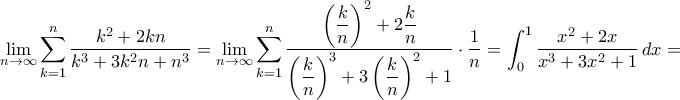
![\displaystyle{=\dfrac {1}{3} \int _0^1\dfrac {(x^3+3x^2+1)'}{x^3+3x^2+1} \,dx= \dfrac {1}{3} \left [\ln |x^3+3x^2+1|\right ]_0^1= \dfrac {1}{3} \ln 5 \displaystyle{=\dfrac {1}{3} \int _0^1\dfrac {(x^3+3x^2+1)'}{x^3+3x^2+1} \,dx= \dfrac {1}{3} \left [\ln |x^3+3x^2+1|\right ]_0^1= \dfrac {1}{3} \ln 5](/forum/ext/geomar/texintegr/latexrender/pictures/d1be05010dff6cd9768215a338af8143.png)
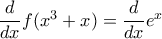 , οπότε από τον κανόνα της άλυσίδας
, οπότε από τον κανόνα της άλυσίδας 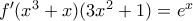 . Οπότε για
. Οπότε για  παίρνουμε
παίρνουμε 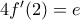 , κ.λπ.
, κ.λπ.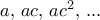 , οι υποθέσεις γράφονται
, οι υποθέσεις γράφονται 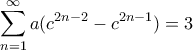 και
και 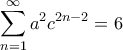 , αντίστοιχα. Ισοδύναμα
, αντίστοιχα. Ισοδύναμα 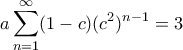 και
και 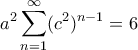 , ή αλλιώς
, ή αλλιώς 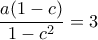 και
και 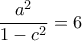 . Iσοδύναμα
. Iσοδύναμα 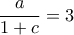 και
και 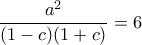 που με διαίρεση κατά μέλη δίνει
που με διαίρεση κατά μέλη δίνει 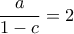 .
.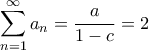 ,
,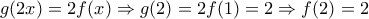
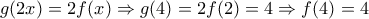
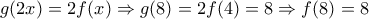
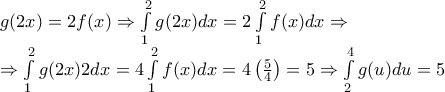
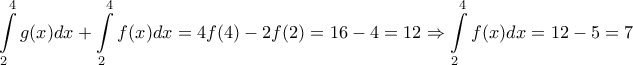
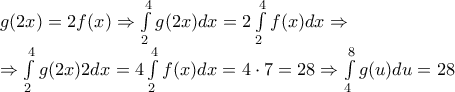
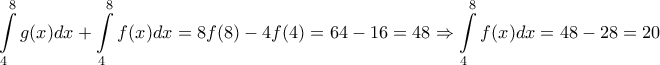
![\begin{array}{l}
\int\limits_1^8 x {f^\prime }(x)dx = \left[ {xf(x)} \right]_1^8 - \int\limits_1^8 {f(x)dx} = 8f(8) - f(1) - \int\limits_1^8 {f(x)dx} = 63 - \int\limits_1^8 {f(x)dx} = \\
\\
= 63 - \left( {\int\limits_1^2 {f(x)dx} + \int\limits_2^4 {f(x)dx} + \int\limits_4^8 {f(x)dx} } \right) = 63 - \left( {\frac{5}{4} + 7 + 20} \right) = \frac{{139}}{4} = \frac{p}{q} \Rightarrow p + q = 143
\end{array} \begin{array}{l}
\int\limits_1^8 x {f^\prime }(x)dx = \left[ {xf(x)} \right]_1^8 - \int\limits_1^8 {f(x)dx} = 8f(8) - f(1) - \int\limits_1^8 {f(x)dx} = 63 - \int\limits_1^8 {f(x)dx} = \\
\\
= 63 - \left( {\int\limits_1^2 {f(x)dx} + \int\limits_2^4 {f(x)dx} + \int\limits_4^8 {f(x)dx} } \right) = 63 - \left( {\frac{5}{4} + 7 + 20} \right) = \frac{{139}}{4} = \frac{p}{q} \Rightarrow p + q = 143
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/c19e22cf6ce0e37804f21f2e0eb20e45.png)
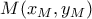 το σημείο που κινείται στο μέσο της χορδής η οποία ορίζεται από την ευθεία
το σημείο που κινείται στο μέσο της χορδής η οποία ορίζεται από την ευθεία
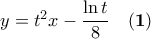
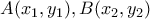 τα άκρα άκρα της χορδής πάνω στην
τα άκρα άκρα της χορδής πάνω στην 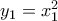 ,
, 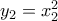 .
. ,
,  ανήκουν στη χορδή ικανοποιούν την (1):
ανήκουν στη χορδή ικανοποιούν την (1):
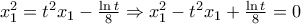
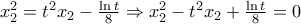
 είναι οι ρίζες της β'βάθμιας
είναι οι ρίζες της β'βάθμιας
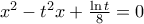
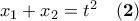
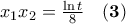
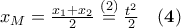
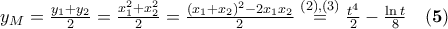
 γράφεται παραμετρικά ως
γράφεται παραμετρικά ως 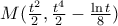 .
.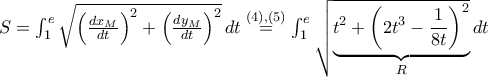
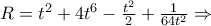
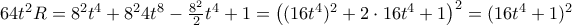
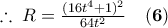
![S = \int_1^e \frac{16t^4+1}{8t} \, dt = \int_1^e 2t^3 + \frac{1}{8t} \, dt = 2\left[\frac{t^4}{4} \right]_1^e + \frac{1}{8}\left[\ln t \right]_1^e = \boxed{\frac{e^4}{2} - \frac{3}{8}} S = \int_1^e \frac{16t^4+1}{8t} \, dt = \int_1^e 2t^3 + \frac{1}{8t} \, dt = 2\left[\frac{t^4}{4} \right]_1^e + \frac{1}{8}\left[\ln t \right]_1^e = \boxed{\frac{e^4}{2} - \frac{3}{8}}](/forum/ext/geomar/texintegr/latexrender/pictures/ea1c6c8423e98704072dd8c53b4d0b39.png)