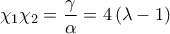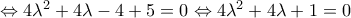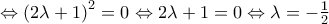Δίνεται η συνάρτηση
 , με
, με 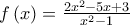
α) Να βρείτε το πεδίο ορισμού της
 . (Μονάδες 5)
. (Μονάδες 5)β) Να παραγοντοποιήσετε το τριώνυμο
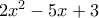 . (Μονάδες 10)
. (Μονάδες 10)γ) Να αποδείξετε ότι για κάθε
 ισχύει:
ισχύει: 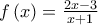 (Μονάδες 10)
(Μονάδες 10)ΠΡΟΤΕΙΝΟΜΕΝΗ ΛΥΣΗ
α) Για να έχει νόημα πραγματικού αριθμού το κλάσμα
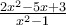 πρέπει και αρκεί:
πρέπει και αρκεί: 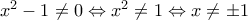 .
. Επομένως το σύνολο ορισμού της συνάρτησης
 είναι το
είναι το 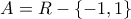 .
.β) Το τριώνυμο
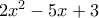 έχει διακρίνουσα
έχει διακρίνουσα 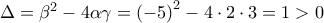 , οπότε έχει δύο άνισες πραγματικές ρίζες, τις
, οπότε έχει δύο άνισες πραγματικές ρίζες, τις 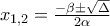
Είναι
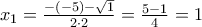 και
και 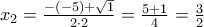
Άρα
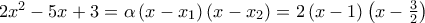 .
.γ) Για κάθε
 ισχύει:
ισχύει: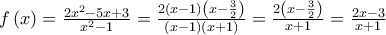

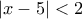 (Μονάδες 8)
(Μονάδες 8)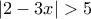 (Μονάδες 8)
(Μονάδες 8)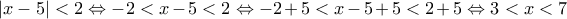
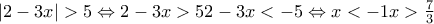
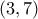
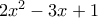 .
. για τις οποίες :
για τις οποίες : 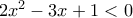 (Μονάδες 5)
(Μονάδες 5)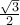 και
και 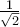 είναι λύσεις της ανίσωσης:
είναι λύσεις της ανίσωσης: 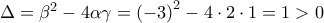 , οπότε έχουμε δύο άνισες πραγματικές ρίζες, τις
, οπότε έχουμε δύο άνισες πραγματικές ρίζες, τις 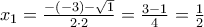 και
και 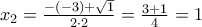 .
.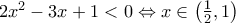 .
. 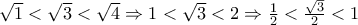 άρα
άρα 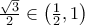 ( σε αυτήν την γραμμή αγνοείστε τα κόκκινα...δεν ξέρω πως βγαίνουν)
( σε αυτήν την γραμμή αγνοείστε τα κόκκινα...δεν ξέρω πως βγαίνουν)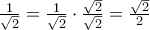 .
.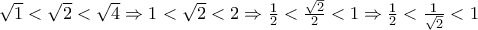 άρα
άρα 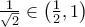 .
. 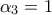 και
και 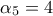
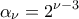 . (Μονάδες 12)
. (Μονάδες 12)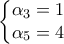

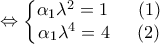
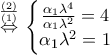
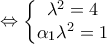
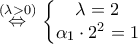
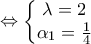
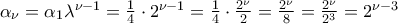
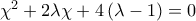 με παράμετρο
με παράμετρο .
. ισχύει:
ισχύει: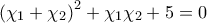
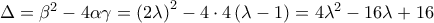
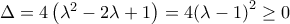
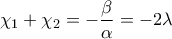 και
και