Σελίδα 1 από 15
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 9:13 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Ξεκινάμε μια προσπάθεια να λυθούν όσο το δυνατόν περισσότερες ασκήσεις γεωμετρίας από την τράπεζα θεμάτων (Τέταρτο θέμα). Για να μην έχουμε επαναλήψεις, ας ξεκινήσουμε με την σειρά, όπως έχουν δημοσιευθεί οι ασκήσεις και ας γράφουμε την πρόθεσή μας να ασχοληθούμε.
Ξεκινάω με την πρώτη κατά σειρά (την 3817)
AΣΚΗΣΗ:
Δίνεται οξυγώνιο τρίγωνο

και στο εξωτερικό του σχηματίζονται τα τετράγωνα

και

. Να αποδείξετε οτι:
(α)

(β)

(γ) Η

είναι κάθετη στην
 ΛΥΣΗ
ΛΥΣΗ

- 3817(β).png (15.41 KiB) Προβλήθηκε 22103 φορές
(α) Έχουμε:

(β) Τα τρίγωνα

και

έχουν:

, ως πλευρές τετραγώνου

, επίσης ως πλευρές τετραγώνου

Άρα τα τρίγωνα είναι ίσα. Άρα θα έχουν και

(γ) Από το ορθογώνιο τρίγωνο

έχουμε :

, (1)
Όμως

, (λόγω της ισότητας των τριγώνων του (β) ερωτήματος) και

,
(ως κατακορυφήν). Άρα η σχέση (1) γράφεται:

και άρα η

είναι κάθετη στην

Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 9:16 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 3820: Δίνεται ορθογώνιο τρίγωνο

με την γωνία

ορθή και τυχαίο σημείο
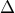
της πλευράς

.
Έστω

τα μέσα των

αντίστοιχα. Να αποδείξετε ότι:
(α) Το τετράπλευρο

είναι παραλληλόγραμμο
(β) Το τετράπλευρο

είναι ισοσκελές τραπέζιο
(γ) Η διάμεσος του τραπεζίου

είναι ίση με
 ΛΥΣΗ
ΛΥΣΗ

- 3820.png (3.61 KiB) Προβλήθηκε 21973 φορές
(α) Στο τρίγωνο

η

ενώνει τα μέσα των πλευρών

και

. Άρα

.
Eπίσης στο ίδιο τρίγωνο, η

ενώνει τα μέσα των πλευρών

και

και άρα

.
Συνεπώς το τετράπλευρο

είναι παραλληλόγραμμο διότι έχει τις απέναντι πλευρές του παράλληλες.
(β) Δείξαμε από το (α) ερώτημα, ότι

. Για να δείξουμε ότι το τετράπλευρο

είναι τραπέζιο, αρκεί να δείξουμε ότι οι πλευρές
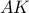
και

δεν είναι παράλληλες. Πράγματι αν ήταν

, τότε από το σημείο

θα είχαμε δύο παράλληλες προς την

, μία
την

και την άλλη την

(λόγω του παραλληλογράμμου

). Τούτο όμως αντίκειται στο Ευκλείδειο αίτημα.
Δείξαμε λοιπόν ότι το τετράπλευρο

είναι τραπέζιο. Επίσης έχουμε:

(ως απέναντι πλευρές παραλληλογράμμου) και

(διότι η
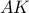
είναι διάμεσος προς την υποτείνουσα του ορθ. τριγώνου

). Άρα

Συμπεραίνουμε λοιπόν ότι

και άρα το τραπέζιο

είναι ισοσκελές.
(γ) Για την διάμεσο του πιο πάνω τραπεζίου έχουμε:

Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 9:42 pm
από george visvikis
(Παίρνω την επόμενη κατά σειρά την 3822. Θα δημοσιευτεί μόλις τελειώσω)
Άσκηση 3822
Δίνεται παραλληλόγραμμο

με τη γωνία του

να είναι ίση με

και το ύψος του

. Έστω

σημείο της

ώστε

.
α) Να αποδείξετε ότι το τετράπλευρο

είναι ισοσκελές τραπέζιο. (
Μονάδες 
)
β) Να υπολογίσετε τις γωνίες του τραπεζίου

(
Μονάδες 
)
γ) Αν

το μέσο του

να αποδείξετε ότι

(
Μονάδες 
)
Λύση
α) Η

είναι μεσοκάθετος του

, άρα το τρίγωνο

είναι ισοσκελές (

). Αλλά

, από το παραλληλόγραμμο.
Οπότε έχουμε

,

, ενώ οι

δεν είναι παράλληλες, αφού

. Άρα το

είναι ισοσκελές τραπέζιο.

- 4_3822.png (12.85 KiB) Προβλήθηκε 21892 φορές
β) Είναι

Εξάλλου από το παραλληλόγραμμο

είναι

Επομένως οι γωνίες του ισοσκελούς τραπεζίου είναι:

,
 γ)
γ) Το

είναι και μέσο της

, αφού οι διαγώνιοι του παραλληλογράμμου διχοτομούνται. Άρα η

είναι διάμεσος του ορθογωνίου τριγώνου

, οπότε:

Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 10:01 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 3824: Δίνεται ορθογώνιο τρίγωνο

με

και

. Φέρνουμε το ύψος του

και την διάμεσό του

. Aπό το

φέρνουμε κάθετη στην ευθεία

, η οποία την τέμνει στο

. Nα αποδείξετε ότι:
(α) Το τρίγωνο

είναι ισόπλευρο.
(β)

(γ) Το

είναι ισοσκελές τραπέζιο.
ΛΥΣΗ

- 3824.png (4.03 KiB) Προβλήθηκε 21777 φορές
(α) Αφού

, άρα

. Επίσης αφού η

είναι διάμεσος προς την υποτείνουσα στο ορθογώνιο
τρίγωνο

, έπεται ότι

. Άρα

και άρα το τρίγωνο

είναι ισόπλευρο.
(β) Τα ορθογώνια τρίγωνα

και

έχουν:

(διότι

) και

, ως κατακορυφήν)
Άρα τα εν λόγω τρίγωνα είναι ίσα και άρα θα έχουν και

. Όμως αφού το τρίγωνο

είναι ισόπλευρο, το ύψος του

θα
είναι και διάμεσος. Άρα

.
(γ) Αφού

, (εφόσον το τρίγωνο

είναι ισοσκελές). Άρα


, (ως κατακορυφήν). Όμως

(από την ισότητα των πιο πάνω τριγώνων). Άρα

.
Aφού λοιπόν

, θα είναι

. Θα δείξουμε τώρα ότι οι ευθείες

και

δεν είναι παράλληλες. Έχουμε:

, (διότι αφού η

είναι ύψος στο ισόπλευρο τρίγωνο

, θα είναι και διχοτόμος.)
Επίσης

(αφού

λόγω της ισότητας των τριγώνων

και

Έχουμε λοιπόν:


. Άρα οι ευθείες

και

δεν είναι παράλληλες και άρα το

είναι τραπέζιο.
Επίσης από την ισότητα των τριγώνων

και

έπεται ότι

. Άρα το τραπέζιο

είναι ισοσκελές.
ΣΗΜ: Θα μπορούσαμε και αλλιώς να δείξουμε ότι οι ευθείες

δεν είναι παράλληλες, ως εξής: Αν ήταν παράλληλες, τότε θα έπρεπε

, δηλαδή

, που όμως είναι άτοπο.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 10:30 pm
από hlkampel
ΑΣΚΗΣΗ 3825
Δίνεται τρίγωνο

με

.
Φέρουμε τη διχοτόμο του

και σε τυχαίο σημείο της

φέρουμε ευθεία κάθετη στη διχοτόμο

, η οποία τέμνει
τις
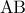
και

στα σημεία
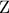
και

αντίστοιχα και την προέκταση της

στο σημείο

.
Να αποδείξετε ότι:
α)

β)

γ)
 Λύση
Λύση
α) Η

είναι εξωτερική του τριγώνου

, έτσι είναι:

β) Το τρίγωνο

είναι ισοσκελές αφού η

είναι διχοτόμος και ύψος, έτσι

Τα τρίγωνα

και

είναι είσαι αφού έχουν:

από την

,

κοινή πλευρά και

,
άρα και

γ) Από το τρίγωνο

είναι:




Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 11:11 pm
από george visvikis
Άσκηση 3903
Δίνεται τετράπλευρο

με

και

. Αν

είναι το σημείο τομής των προεκτάσεων των

και
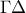
και

είναι το σημείο τομής των προεκτάσεων των

και

να αποδείξετε ότι:
α) Η

είναι διχοτόμος της γωνίας

(
Μονάδες 
)
β) 
(
Μονάδες 
)
γ) 
(
Μονάδες 
)
Λύση:
α) Τα τρίγωνα

είναι ίσα επειδή έχουν την

κοινή και

,

από την υπόθεση (
Π-Π-Π). Οπότε θα είναι

, δηλαδή η

είναι διχοτόμος της γωνίας


- 4_3903.png (10.06 KiB) Προβλήθηκε 21587 φορές
β) 
(ως κατακορυφήν).

(ως παραπληρωματικές των ίσων γωνιών

του ισοσκελούς τριγώνου

)
Άρα τα τρίγωνα

είναι ίσα (
Γ-Π-Γ). Οπότε
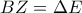
και κατά συνέπεια,
 γ)
γ) Στα ισοσκελή τρίγωνα

η διχοτόμος της γωνίας

θα είναι μεσοκάθετη στις βάσεις.
Άρα

, ως κάθετες στην ίδια ευθεία.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 11:19 pm
από hlkampel
Άσκηση 3904
α) Σε ορθογώνιο

θεωρούμε

τα μέσα των πλευρών του
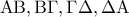
αντίστοιχα. Να αποδείξετε ότι το τετράπλευρο

είναι ρόμβος.
β) Σε ένα τετράπλευρο

τα μέσα

των πλευρών του
αντίστοιχα είναι κορυφές ρόμβου.
Το τετράπλευρο

, πρέπει να είναι απαραίτητα ορθογώνιο; Να τεκμηριώσετε τη θετική ή αρνητική σας απάντηση.
Λύση
α) Το

είναι παραλληλόγραμμο αφού ενώνει τα μέσα των πλευρών του ορθογωνίου

(από εφαρμογή 1 σελ. 106)
Είναι

και

αφού τα τμήματα

ενώνουν τα μέσα δύο πλευρών των τριγώνων

και

αντίστοιχα.
Όμως

ως διαγώνιοι ορθογωνίου, έτσι και

Άρα το

είναι ρόμβος αφού είναι παραλληλόγραμμο με δύο διαδοχικές πλευρές ίσες.
β) Αν το

είναι ρόμβος τότε το τετράπλευρο
 δεν
δεν είναι απαραίτητα ορθογώνιο αφού αρκεί οι διαγώνιοι του να είναι ίσοι ώστε να συμβαίνουν όλα τα παραπάνω.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 11:50 pm
από Μπάμπης Στεργίου
ΠΡΟΒΛΗΜΑ 3906
Εκτός τριγώνου

κατασκευάζουμε τετράγωνα

. Αν

το μέσο του
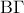
και
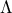
σημείο στην προέκταση της

τέτοιο , ώστε

, να αποδείξετε ότι:
α)

. (Μονάδες 10)
β) 0ι γωνίες

είναι ίσες. (Μονάδες 10)
γ) Η προέκταση της

(προς το

) τέμνει κάθετα την

. (Μονάδες 5)
ΛΥΣΗ
α) To

είναι παραλληλόγραμμο, διότι οι διαγώνιες

διχοτομούνται. Επομένως

β) Οι γωνίες

είναι ίσες, διότι είναι παραπληρωματικές της γωνίας


- 2014-5-26, TRAP.PNG (21.62 KiB) Προβλήθηκε 21547 φορές
γ) Τα τρίγωνα

είναι ίσα, διότι

Επομένως :

,
διότι

.
( Με πολλά προβλήματα στη μετατροπή, αλλά θα δω τι φταίει)
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Δευ Μάιος 26, 2014 11:54 pm
από hlkampel
Άσκηση 3908
Δυο ίσοι κύκλοι

και

εφάπτονται εξωτερικά στο σημείο

. Αν

και

είναι τα εφαπτόμενα τμήματα από το σημείο

στον κύκλο

να αποδείξετε ότι:
α)

β)

γ) Το τετράπλευρο

είναι ρόμβος.
Λύση
α) Τα τρίγωνα

και

είναι ίσα αφού έχουν:

κοινή πλευρά,
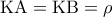
και

ως εφαπτόμενα τμήματα.
Έτσι

Τα τρίγωνα

και

είναι ίσα αφού έχουν:

κοινή πλευρά,

από

και

ως εφαπτόμενα τμήματα.
Άρα και

β) Είναι

(ακτίνα στο σημείο επαφής),

και

Άρα

διότι στο ορθ. τρίγωνο

η μία κάθετη πλευρά

είναι το μισό της υποτείνουσας

.
γ) Είναι

αφού η

είναι διάμεσος στην υποτείνουσα του ορθ. τριγώνου

.
Ομοίως είναι και

Άρα

δηλαδή το τετράπλευρο

είναι ρόμβος αφού έχει όλες τις πλευρές του ίσες.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 12:00 am
από Doloros
Επειδή δεν έχω την δυνατότητα να συμμετέχω με σωστό τρόπο στην αξιέπαινη προσπάθεια σας δίδω μια.
Αν δεν είναι εδώ η θέση της δεν με πειράζει να την βάλετε όπου θέλετε ή και να αποκαθηλωθεί πλήρως.
Άσκηση 3762
Δίδεται τετράγωνο

. Έστω

το συμμετρικό του

ως προς το

και
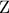
είναι το μέσο της

.
Να αποδείξετε ότι :
α)

(μ 8)
β) τα τρίγωνα

είναι ίσα (μ9)
γ) Η

είναι κάθετη στην

(μ 8)
Λύση

- 4_3762.png (11.01 KiB) Προβλήθηκε 21601 φορές
α) Οι ευθείες

είναι παράλληλες ως κάθετες στην ευθεία

και αφού στο τρίγωνο

το σημείο

είναι μέσο της πλευράς

κι αυτό λόγω συμμετρίας των

ως προς το

, θα είναι και
το

μέσο της πλευράς

. Άμεση συνέπεια

.
β) Επειδή και

λόγω της

θα είναι :

. Τα ορθογώνια τρίγωνα

έχουν :

ως πλευρές του τετραγώνου και λόγω της


. Δηλαδή
τις κάθετες πλευρές τους ίσες άρα θα είναι ίσα .
γ) Επειδή τώρα τα ορθογώνια τρίγωνα

είναι ίσα θα έχουν και όλα τα υπόλοιπα αντίστοιχα στοιχεία τους ένα προς ένα ίσα και άρα

Όμως στο ορθογώνιο τρίγωνο

οι οξείες του γωνίες έχουν άθροισμα

, δηλαδή

, οπότε λόγω της

έχουμε :

(4).
Αν τώρα πούμε

το σημείο τομής της

με την

στο τρίγωνο

το άθροισμα δύο γωνιών του είναι λόγω της


και άρα η γωνία του

και έτσι

.
Φιλικά Νίκος
Υ.Γ.
Η άσκηση έχει κι άλλες ωραίες λύσεις αλλά επειδή δεν πρέπει να μπερδεύουμε τα παιδιά έδωσα την πιο "ανώδυνη" ( κατά την δική μου άποψη)
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 12:19 am
από george visvikis
Άσκηση 3911
α) Σε ισοσκελές τραπέζιο

θεωρούμε

τα μέσα των πλευρών του
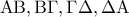
αντίστοιχα. Να αποδείξετε ότι το τετράπλευρο

είναι ρόμβος.
β) Σε ένα τετράπλευρο

τα μέσα

των πλευρών του
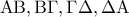
αντίστοιχα είναι κορυφές ρόμβου.
Για να σχηματίζεται ρόμβος το

, πρέπει να είναι ισοσκελές τραπέζιο; Να τεκμηριώσετε τη θετική ή αρνητική σας απάντηση.
Η άσκηση είναι παρόμοια με την 3904 που έλυσε ο Ηλίας πιο πάνω.
Τα πρώτα ερωτήματα στηρίζονται στο γεγονός ότι οι διαγώνιοι του ορθογωνίου είναι ίσες, όπως και οι διαγώνιοι του ισοσκελούς τραπεζίου.
Στο β) ερώτημα, ακριβώς ίδια αντιμετώπιση όπως και στο 3904.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 12:44 am
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 3915: (α) Σε ρόμβο

θεωρούμε

τα μέσα των πλευρών του

αντίστοιχα.
Να αποδείξετε ότι το τετράπλευρο
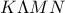
είναι ορθογώνιο.
(β) Να αποδείξετε ότι τα μέσα των πλευρών ενός ορθογωνίου είναι κορυφές ρόμβου.
ΛΥΣΗ
(α)

- 3915(α).png (6.58 KiB) Προβλήθηκε 21365 φορές
Η

ενώνει τα μέσα των πλευρών

και

του τριγώνου

. Άρα

. Ομοίως έχουμε ότι:

. Άρα συμπεραίνουμε ότι

και άρα το τετράπλευρο
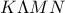
είναι παραλληλόγραμμο.
Επίσης αφού είναι

και

, (διότι η

ενώνει τα μέσα δύο πλευρών στο τρίγωνο

), και
αφού

(διότι οι διαγώνιοι ρόμβου τέμνονται καθέτως), τότε θα είναι και

, εφόσον οι γωνίες

και

έχουν τις πλευρές τους παράλληλες μία προς μία. Δείξαμε λοιπόν ότι το παραλληλόγραμμο
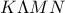
έχει μία γωνία ορθή
άρα είναι ορθογώνιο.
(β)

- 3915(β).png (3.82 KiB) Προβλήθηκε 21365 φορές
Συγκρίνουμε τα ορθογώνια τρίγωνα

και

, τα οποία έχουν:

(διότι το

είναι μέσον του

) και

(ως μισά των ίσων τμημάτων

και

). Άρα τα τρίγωνα αυτά
είναι ίσα και άρα θα έχουν και

. Όμως επί πλέον το τετράπλευρο

είναι παραλληλόγραμμο [διότι:

, (αφού ενώνει τα μέσα δύο πλευρών του τριγώνου

) και

, (αφού ενώνει
τα μέσα δύο πλευρών του τριγώνου
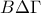
). Δηλαδή είναι

]. Έτσι , αφού το παραλληλόγραμμο
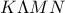
έχει
δύο διαδοχικές πλευρές του ίσες, άρα θα είναι ρόμβος.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 12:53 am
από hlkampel
Άσκηση 3919
Δίνεται ισοσκελές τρίγωνο

με

και

τα ύψη του. Να αποδείξετε ότι:
α)
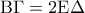
β)

γ) Το τετράπλευρο

δ)
 Λύση
Λύση
α) Το ύψος

που αντιστοιχεί στη βάση
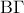
του ισοσκελούς τριγώνου είναι και διάμεσος, δηλαδή το

είναι μέσο του
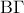
.
Στο ορθ. τρίγωνο

το

είναι διάμεσος στην υποτείνουσα
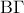
, έτσι

.
β) Το τετράπλευρο

είναι εγγράψιμο αφού η πλευρά του
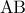
φαίνεται από τις απέναντι κορυφές

υπό ορθή γωνία.
Άρα

(Σημείωση: Μάλλον κάτι άλλο είχε στο μυαλό του ο θεματοδότης)
γ) Το τετράπλευρο

είναι εγγράψιμο από το (β) ερώτημα.
δ) Είναι

αφού το τετράπλευρο

είναι εγγράψιμο.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 1:21 am
από hlkampel
Άσκηση 3926
Δίνεται ισοσκελές τρίγωνο

με

, τυχαίο σημείο

της βάσης του
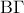
και το ύψος του

.
Από το

φέρουμε κάθετες

και

στις

και

αντίστοιχα. Να αποδείξετε ότι:
α) Το τετράπλευρο

είναι ορθογώνιο.
β)

γ) Το άθροισμα
 Λύση
Λύση
α) Είναι

, δηλαδή το τετράπλευρο

είναι ορθογώνιο αφού έχει τρείς ορθές γωνίες.
β) Είναι

ως κάθετες στη

, έτσι

ως εντός εκτός και επί τα αυτά.
Τα ορθ. τρίγωνα

και

είναι ίσα αφού έχουν

κοινή πλευρά και

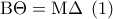
.
γ) Είναι

από το ορθογώνιο

.

Edit: Έγινε διόρθωση τυπογραφικού. Ευχαριστώ τον Γιάννη (παρακάτω) για τον εντοπισμό.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 3:53 am
από pana1333
Άσκηση 3932

- σχήμα.png (12.68 KiB) Προβλήθηκε 21276 φορές
α) Επειδή στο τρίγωνο

είναι

μέσο της πλευράς

και

μέσο της πλευράς

είναι

και

αφού

μέσο της πλευράς

. Επομένως η πλευρά

είναι παράλληλη και ίση με την πλευρά

που σημαίνει ότι το τετράπλευρο

είναι παραλληλόγραμμο. Επομένως

(1)
β) Αφού είναι

τότε είναι

ως εντός εναλλάξ, και επειδή

αφού

διχοτόμος θα είναι και

που σημαίνει ότι το τρίγωνο

είναι ισοσκελές. Άρα και

(2). Ομοίως είναι

ως εντός εναλλάξ διότι

αφού το

είναι παραλληλόγραμμο και επειδή

και

ως κατακορυφήν θα είναι και

. Συνεπώς το τρίγωνο

είναι ισοσκελές. Επομένως και

(3).
γ)Με τη βοήθεια των ισοτήτων (2),(3),(1) έχουμε

.
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 4:28 am
από pana1333
Άσκηση 3938
α) Στο τρίγωνο

είναι

μέσο της πλευράς

και
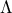
μέσο της

. Τότε είναι
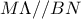
και

(1). Επομένως και

. Αντιστρόφως στο τρίγωνο

αφού είναι

μέσο της

και

τότε το

είναι μέσο της πλευράς

και επομένως θα είναι και

(2).
β) Η γωνία

και η

είναι παραπληρωματικές. Επομένως είναι

(3). Επίσης είναι

(4) ως κατακορυφήν. Επομένως στο τρίγωνο

έχουμε ότι

(5)
Από τις σχέσεις (3) και (5) προκύπτει το ζητούμενο

γ) Από τις σχέσεις (1) και (2) έχουμε ότι

Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 7:43 am
από STOPJOHN
Kαλημέρα σε όλους
Η λύση της άσκησης

Γεωμετρίας χρειάζεται διόρθωση Να γραφτεί

φιλικά
Γιάννης
Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 8:13 am
από hlkampel
Άσκηση 3945
Δίνεται τρίγωνο

με

.
Έστω

διάμεσος του

και

τα μέσα των

και
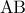
αντίστοιχα.
Να αποδείξετε ότι:
α)

β)

γ) Η

είναι διχοτόμος της γωνίας
 Λύση
Λύση
α) Είναι

αφού το

είναι μέσο της
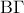
και

από υπόθεση.
Έτσι

. Δηλαδή το τρίγωνο

είναι ισοσκελές οπότε

β) Είναι

και

αφού το τμήμα

ενώνει τα μέσα των πλευρών

του τριγώνου

και ισχύει

.
Έτσι

γ) Τα τρίγωνα

και

είναι ίσα αφού έχουν:

κοινή πλευρά,

από (β) ερώτημα και

αφού

ως εντός εναλλάξ των

που τέμνονται από την

και

από (α) ερώτημα.
Άρα

δηλαδή η

είναι διχοτόμος της γωνίας

Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 8:49 am
από hlkampel
Άσκηση 3948
Δίνεται τετράπλευρο

με

και

τα μέσα των

αντίστοιχα.
Αν οι προεκτάσεις των ΑΒ και ΔΓ τέμνουν την προέκταση της

στα σημεία

και
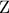
αντίστοιχα να αποδείξετε ότι:
α)

β)
 Λύση
Λύση
α) Είναι

και

γιατί τα τμήματα

ενώνουν τα μέσα δύο πλευρών των τριγώνων

και

αντίστοιχα.
Όμως είναι

από την υπόθεση, έτσι από

β) Αφού

το τρίγωνο

είναι ισοσκελές, οπότε

Είναι

ως εντός εναλλάξ των παραλλήλων

που τέμνονται από την

.

ως εντός εκτός και επί τα αυτά των παραλλήλων

που τέμνονται από την

.
Από τις

λόγω της

συμπεραίνουμε ότι

Re: ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ -ΤΕΤΑΡΤΟ ΘΕΜΑ
Δημοσιεύτηκε: Τρί Μάιος 27, 2014 8:53 am
από Doloros
hlkampel έγραψε:Άσκηση 3945
γ) Τα τρίγωνα

και

είναι ίσα αφού έχουν:

κοινή πλευρά,

από (β) ερώτημα και

αφού

ως εντός εναλλάξ των

που τέμνονται από την

και

από (α) ερώτημα.
Άρα

δηλαδή η

είναι διχοτόμος της γωνίας

Μια εναλλακτική πρόταση για το τρίτο ερώτημα

- 3945.png (18.75 KiB) Προβλήθηκε 21067 φορές
Αφού από το β) ερώτημα έχουμε

θα είναι

, ως εντός εναλλάξ των ευθειών

τεμνομένων υπό της

. Όμως από το α) ερώτημα :

και συνεπώς

.
Φιλικά Νίκος
 και στο εξωτερικό του σχηματίζονται τα τετράγωνα
και στο εξωτερικό του σχηματίζονται τα τετράγωνα  και
και  . Να αποδείξετε οτι:
. Να αποδείξετε οτι:

 είναι κάθετη στην
είναι κάθετη στην 

 και
και  έχουν:
έχουν: , ως πλευρές τετραγώνου
, ως πλευρές τετραγώνου , επίσης ως πλευρές τετραγώνου
, επίσης ως πλευρές τετραγώνου

 έχουμε :
έχουμε :  , (1)
, (1) , (λόγω της ισότητας των τριγώνων του (β) ερωτήματος) και
, (λόγω της ισότητας των τριγώνων του (β) ερωτήματος) και  ,
,  και άρα η
και άρα η  είναι κάθετη στην
είναι κάθετη στην 
 και στο εξωτερικό του σχηματίζονται τα τετράγωνα
και στο εξωτερικό του σχηματίζονται τα τετράγωνα  και
και  . Να αποδείξετε οτι:
. Να αποδείξετε οτι:

 είναι κάθετη στην
είναι κάθετη στην 

 και
και  έχουν:
έχουν: , ως πλευρές τετραγώνου
, ως πλευρές τετραγώνου , επίσης ως πλευρές τετραγώνου
, επίσης ως πλευρές τετραγώνου

 έχουμε :
έχουμε :  , (1)
, (1) , (λόγω της ισότητας των τριγώνων του (β) ερωτήματος) και
, (λόγω της ισότητας των τριγώνων του (β) ερωτήματος) και  ,
,  και άρα η
και άρα η  είναι κάθετη στην
είναι κάθετη στην 
 ορθή και τυχαίο σημείο
ορθή και τυχαίο σημείο  της πλευράς
της πλευράς  .
. τα μέσα των
τα μέσα των  αντίστοιχα. Να αποδείξετε ότι:
αντίστοιχα. Να αποδείξετε ότι: είναι παραλληλόγραμμο
είναι παραλληλόγραμμο είναι ισοσκελές τραπέζιο
είναι ισοσκελές τραπέζιο
 η
η  ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  και
και  . Άρα
. Άρα  .
. ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  και
και  και άρα
και άρα  .
. . Για να δείξουμε ότι το τετράπλευρο
. Για να δείξουμε ότι το τετράπλευρο  είναι τραπέζιο, αρκεί να δείξουμε ότι οι πλευρές
είναι τραπέζιο, αρκεί να δείξουμε ότι οι πλευρές 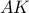 και
και  , τότε από το σημείο
, τότε από το σημείο  θα είχαμε δύο παράλληλες προς την
θα είχαμε δύο παράλληλες προς την  και την άλλη την
και την άλλη την  (λόγω του παραλληλογράμμου
(λόγω του παραλληλογράμμου  (ως απέναντι πλευρές παραλληλογράμμου) και
(ως απέναντι πλευρές παραλληλογράμμου) και (διότι η
(διότι η  ). Άρα
). Άρα 
 και άρα το τραπέζιο
και άρα το τραπέζιο 
 με τη γωνία του
με τη γωνία του  να είναι ίση με
να είναι ίση με  και το ύψος του
και το ύψος του  . Έστω
. Έστω  σημείο της
σημείο της  ώστε
ώστε  .
. είναι ισοσκελές τραπέζιο. (Μονάδες
είναι ισοσκελές τραπέζιο. (Μονάδες  )
) )
) το μέσο του
το μέσο του  να αποδείξετε ότι
να αποδείξετε ότι  (Μονάδες
(Μονάδες  , άρα το τρίγωνο
, άρα το τρίγωνο  είναι ισοσκελές (
είναι ισοσκελές ( ). Αλλά
). Αλλά  , από το παραλληλόγραμμο.
, από το παραλληλόγραμμο. ,
,  , ενώ οι
, ενώ οι  δεν είναι παράλληλες, αφού
δεν είναι παράλληλες, αφού  . Άρα το
. Άρα το 

 ,
, 
 , αφού οι διαγώνιοι του παραλληλογράμμου διχοτομούνται. Άρα η
, αφού οι διαγώνιοι του παραλληλογράμμου διχοτομούνται. Άρα η  είναι διάμεσος του ορθογωνίου τριγώνου
είναι διάμεσος του ορθογωνίου τριγώνου  , οπότε:
, οπότε: 
 και
και  . Φέρνουμε το ύψος του
. Φέρνουμε το ύψος του 
 . Aπό το
. Aπό το  φέρνουμε κάθετη στην ευθεία
φέρνουμε κάθετη στην ευθεία  . Nα αποδείξετε ότι:
. Nα αποδείξετε ότι: είναι ισόπλευρο.
είναι ισόπλευρο.
 είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο. . Επίσης αφού η
. Επίσης αφού η  . Άρα
. Άρα  και άρα το τρίγωνο
και άρα το τρίγωνο  και
και  έχουν:
έχουν:  (διότι
(διότι  ) και
) και  , ως κατακορυφήν)
, ως κατακορυφήν) . Όμως αφού το τρίγωνο
. Όμως αφού το τρίγωνο  είναι ισόπλευρο, το ύψος του
είναι ισόπλευρο, το ύψος του  .
. , (εφόσον το τρίγωνο
, (εφόσον το τρίγωνο  είναι ισοσκελές). Άρα
είναι ισοσκελές). Άρα 
 , (ως κατακορυφήν). Όμως
, (ως κατακορυφήν). Όμως  .
. , θα είναι
, θα είναι  . Θα δείξουμε τώρα ότι οι ευθείες
. Θα δείξουμε τώρα ότι οι ευθείες  και
και  , (διότι αφού η
, (διότι αφού η  (αφού
(αφού  λόγω της ισότητας των τριγώνων
λόγω της ισότητας των τριγώνων  και
και 

 . Άρα οι ευθείες
. Άρα οι ευθείες  και
και  έπεται ότι
έπεται ότι  . Άρα το τραπέζιο
. Άρα το τραπέζιο  δεν είναι παράλληλες, ως εξής: Αν ήταν παράλληλες, τότε θα έπρεπε
δεν είναι παράλληλες, ως εξής: Αν ήταν παράλληλες, τότε θα έπρεπε , δηλαδή
, δηλαδή  , που όμως είναι άτοπο.
, που όμως είναι άτοπο. με
με  .
.  και σε τυχαίο σημείο της
και σε τυχαίο σημείο της  φέρουμε ευθεία κάθετη στη διχοτόμο
φέρουμε ευθεία κάθετη στη διχοτόμο 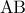 και
και  στα σημεία
στα σημεία 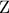 και
και  αντίστοιχα και την προέκταση της
αντίστοιχα και την προέκταση της  στο σημείο
στο σημείο  .
. 


 είναι εξωτερική του τριγώνου
είναι εξωτερική του τριγώνου  , έτσι είναι:
, έτσι είναι:
 είναι ισοσκελές αφού η
είναι ισοσκελές αφού η  είναι διχοτόμος και ύψος, έτσι
είναι διχοτόμος και ύψος, έτσι 
 και
και  είναι είσαι αφού έχουν:
είναι είσαι αφού έχουν: από την
από την  ,
,  ,
, είναι:
είναι:


 και
και  . Αν
. Αν  είναι το σημείο τομής των προεκτάσεων των
είναι το σημείο τομής των προεκτάσεων των  και
και 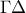 και
και  και
και  να αποδείξετε ότι:
να αποδείξετε ότι: είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  (Μονάδες
(Μονάδες  )
) (Μονάδες
(Μονάδες  (Μονάδες
(Μονάδες  είναι ίσα επειδή έχουν την
είναι ίσα επειδή έχουν την  , δηλαδή η
, δηλαδή η  (ως κατακορυφήν).
(ως κατακορυφήν). (ως παραπληρωματικές των ίσων γωνιών
(ως παραπληρωματικές των ίσων γωνιών  του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  )
) είναι ίσα (Γ-Π-Γ). Οπότε
είναι ίσα (Γ-Π-Γ). Οπότε 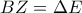 και κατά συνέπεια,
και κατά συνέπεια, 
 η διχοτόμος της γωνίας
η διχοτόμος της γωνίας  θα είναι μεσοκάθετη στις βάσεις.
θα είναι μεσοκάθετη στις βάσεις.  , ως κάθετες στην ίδια ευθεία.
, ως κάθετες στην ίδια ευθεία. θεωρούμε
θεωρούμε  τα μέσα των πλευρών του
τα μέσα των πλευρών του 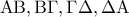 αντίστοιχα. Να αποδείξετε ότι το τετράπλευρο
αντίστοιχα. Να αποδείξετε ότι το τετράπλευρο  είναι ρόμβος.
είναι ρόμβος.  και
και  αφού τα τμήματα
αφού τα τμήματα  ενώνουν τα μέσα δύο πλευρών των τριγώνων
ενώνουν τα μέσα δύο πλευρών των τριγώνων  και
και  ως διαγώνιοι ορθογωνίου, έτσι και
ως διαγώνιοι ορθογωνίου, έτσι και 
 . Αν
. Αν  το μέσο του
το μέσο του 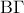 και
και 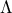 σημείο στην προέκταση της
σημείο στην προέκταση της  τέτοιο , ώστε
τέτοιο , ώστε  , να αποδείξετε ότι:
, να αποδείξετε ότι:  . (Μονάδες 10)
. (Μονάδες 10)  είναι ίσες. (Μονάδες 10)
είναι ίσες. (Μονάδες 10)  (προς το
(προς το  ) τέμνει κάθετα την
) τέμνει κάθετα την  . (Μονάδες 5)
. (Μονάδες 5) είναι παραλληλόγραμμο, διότι οι διαγώνιες
είναι παραλληλόγραμμο, διότι οι διαγώνιες  διχοτομούνται. Επομένως
διχοτομούνται. Επομένως 
 είναι ίσες, διότι είναι παραπληρωματικές της γωνίας
είναι ίσες, διότι είναι παραπληρωματικές της γωνίας 
 είναι ίσα, διότι
είναι ίσα, διότι 
 ,
, .
. και
και  εφάπτονται εξωτερικά στο σημείο
εφάπτονται εξωτερικά στο σημείο  και
και  είναι τα εφαπτόμενα τμήματα από το σημείο
είναι τα εφαπτόμενα τμήματα από το σημείο  στον κύκλο
στον κύκλο 

 είναι ρόμβος.
είναι ρόμβος.  και
και  είναι ίσα αφού έχουν:
είναι ίσα αφού έχουν: κοινή πλευρά,
κοινή πλευρά, 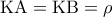 και
και  ως εφαπτόμενα τμήματα.
ως εφαπτόμενα τμήματα.
 και
και  είναι ίσα αφού έχουν:
είναι ίσα αφού έχουν: κοινή πλευρά,
κοινή πλευρά,  από
από  (ακτίνα στο σημείο επαφής),
(ακτίνα στο σημείο επαφής),  και
και 
 είναι το μισό της υποτείνουσας
είναι το μισό της υποτείνουσας  .
. αφού η
αφού η 
 δηλαδή το τετράπλευρο
δηλαδή το τετράπλευρο  ως προς το
ως προς το  .
. (μ 8)
(μ 8) είναι ίσα (μ9)
είναι ίσα (μ9) είναι κάθετη στην
είναι κάθετη στην  είναι παράλληλες ως κάθετες στην ευθεία
είναι παράλληλες ως κάθετες στην ευθεία  και αφού στο τρίγωνο
και αφού στο τρίγωνο  το σημείο
το σημείο  κι αυτό λόγω συμμετρίας των
κι αυτό λόγω συμμετρίας των  ως προς το
ως προς το  . Άμεση συνέπεια
. Άμεση συνέπεια  .
. λόγω της
λόγω της  θα είναι :
θα είναι :  . Τα ορθογώνια τρίγωνα
. Τα ορθογώνια τρίγωνα  έχουν :
έχουν :  ως πλευρές του τετραγώνου και λόγω της
ως πλευρές του τετραγώνου και λόγω της 
 . Δηλαδή
. Δηλαδή 
 οι οξείες του γωνίες έχουν άθροισμα
οι οξείες του γωνίες έχουν άθροισμα  , δηλαδή
, δηλαδή  , οπότε λόγω της
, οπότε λόγω της  έχουμε :
έχουμε :  (4).
(4). το σημείο τομής της
το σημείο τομής της  με την
με την  το άθροισμα δύο γωνιών του είναι λόγω της
το άθροισμα δύο γωνιών του είναι λόγω της 
 και έτσι
και έτσι  .
. θεωρούμε
θεωρούμε  τα μέσα των πλευρών του
τα μέσα των πλευρών του  αντίστοιχα.
αντίστοιχα.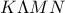 είναι ορθογώνιο.
είναι ορθογώνιο. ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  . Άρα
. Άρα  . Ομοίως έχουμε ότι:
. Ομοίως έχουμε ότι: . Άρα συμπεραίνουμε ότι
. Άρα συμπεραίνουμε ότι  και άρα το τετράπλευρο
και άρα το τετράπλευρο  και
και  , (διότι η
, (διότι η  ενώνει τα μέσα δύο πλευρών στο τρίγωνο
ενώνει τα μέσα δύο πλευρών στο τρίγωνο  (διότι οι διαγώνιοι ρόμβου τέμνονται καθέτως), τότε θα είναι και
(διότι οι διαγώνιοι ρόμβου τέμνονται καθέτως), τότε θα είναι και  , εφόσον οι γωνίες
, εφόσον οι γωνίες  και
και  έχουν τις πλευρές τους παράλληλες μία προς μία. Δείξαμε λοιπόν ότι το παραλληλόγραμμο
έχουν τις πλευρές τους παράλληλες μία προς μία. Δείξαμε λοιπόν ότι το παραλληλόγραμμο  και
και  , τα οποία έχουν:
, τα οποία έχουν:  (διότι το
(διότι το  (ως μισά των ίσων τμημάτων
(ως μισά των ίσων τμημάτων  . Όμως επί πλέον το τετράπλευρο
. Όμως επί πλέον το τετράπλευρο  είναι παραλληλόγραμμο [διότι:
είναι παραλληλόγραμμο [διότι: , (αφού ενώνει τα μέσα δύο πλευρών του τριγώνου
, (αφού ενώνει τα μέσα δύο πλευρών του τριγώνου  , (αφού ενώνει
, (αφού ενώνει 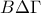 ). Δηλαδή είναι
). Δηλαδή είναι  ]. Έτσι , αφού το παραλληλόγραμμο
]. Έτσι , αφού το παραλληλόγραμμο  και
και  τα ύψη του. Να αποδείξετε ότι:
τα ύψη του. Να αποδείξετε ότι: 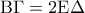



 το
το  είναι διάμεσος στην υποτείνουσα
είναι διάμεσος στην υποτείνουσα  .
. υπό ορθή γωνία.
υπό ορθή γωνία.
 .
.  και
και  στις
στις  και
και  είναι ορθογώνιο.
είναι ορθογώνιο. 

 , δηλαδή το τετράπλευρο
, δηλαδή το τετράπλευρο  ως κάθετες στη
ως κάθετες στη  ως εντός εκτός και επί τα αυτά.
ως εντός εκτός και επί τα αυτά. και
και  είναι ίσα αφού έχουν
είναι ίσα αφού έχουν  κοινή πλευρά και
κοινή πλευρά και 
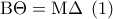 .
.  από το ορθογώνιο
από το ορθογώνιο 
 είναι
είναι  και
και  και
και  αφού
αφού  . Επομένως η πλευρά
. Επομένως η πλευρά  είναι παράλληλη και ίση με την πλευρά
είναι παράλληλη και ίση με την πλευρά  που σημαίνει ότι το τετράπλευρο
που σημαίνει ότι το τετράπλευρο  είναι παραλληλόγραμμο. Επομένως
είναι παραλληλόγραμμο. Επομένως  (1)
(1) τότε είναι
τότε είναι  ως εντός εναλλάξ, και επειδή
ως εντός εναλλάξ, και επειδή  αφού
αφού  διχοτόμος θα είναι και
διχοτόμος θα είναι και  που σημαίνει ότι το τρίγωνο
που σημαίνει ότι το τρίγωνο  είναι ισοσκελές. Άρα και
είναι ισοσκελές. Άρα και  (2). Ομοίως είναι
(2). Ομοίως είναι  ως εντός εναλλάξ διότι
ως εντός εναλλάξ διότι  αφού το
αφού το  είναι παραλληλόγραμμο και επειδή
είναι παραλληλόγραμμο και επειδή  ως κατακορυφήν θα είναι και
ως κατακορυφήν θα είναι και  . Συνεπώς το τρίγωνο
. Συνεπώς το τρίγωνο  είναι ισοσκελές. Επομένως και
είναι ισοσκελές. Επομένως και  (3).
(3). .
.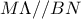 και
και  (1). Επομένως και
(1). Επομένως και  . Αντιστρόφως στο τρίγωνο
. Αντιστρόφως στο τρίγωνο  αφού είναι
αφού είναι  μέσο της
μέσο της  και
και  είναι μέσο της πλευράς
είναι μέσο της πλευράς  και επομένως θα είναι και
και επομένως θα είναι και  (2).
(2). και η
και η  είναι παραπληρωματικές. Επομένως είναι
είναι παραπληρωματικές. Επομένως είναι  (3). Επίσης είναι
(3). Επίσης είναι  (4) ως κατακορυφήν. Επομένως στο τρίγωνο
(4) ως κατακορυφήν. Επομένως στο τρίγωνο  έχουμε ότι
έχουμε ότι  (5)
(5) 

 Γεωμετρίας χρειάζεται διόρθωση Να γραφτεί
Γεωμετρίας χρειάζεται διόρθωση Να γραφτεί 
 .
.  τα μέσα των
τα μέσα των  και
και 


 αφού το
αφού το  από υπόθεση.
από υπόθεση. . Δηλαδή το τρίγωνο
. Δηλαδή το τρίγωνο  είναι ισοσκελές οπότε
είναι ισοσκελές οπότε 
 και
και αφού το τμήμα
αφού το τμήμα  ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  του τριγώνου
του τριγώνου  .
. και
και  είναι ίσα αφού έχουν:
είναι ίσα αφού έχουν: αφού
αφού  ως εντός εναλλάξ των
ως εντός εναλλάξ των  που τέμνονται από την
που τέμνονται από την  δηλαδή η
δηλαδή η  και
και  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα.  στα σημεία
στα σημεία 

 και
και  γιατί τα τμήματα
γιατί τα τμήματα  ενώνουν τα μέσα δύο πλευρών των τριγώνων
ενώνουν τα μέσα δύο πλευρών των τριγώνων  αντίστοιχα.
αντίστοιχα.
 είναι ισοσκελές, οπότε
είναι ισοσκελές, οπότε 
 ως εντός εναλλάξ των παραλλήλων
ως εντός εναλλάξ των παραλλήλων  που τέμνονται από την
που τέμνονται από την  ως εντός εκτός και επί τα αυτά των παραλλήλων
ως εντός εκτός και επί τα αυτά των παραλλήλων  που τέμνονται από την
που τέμνονται από την  .
. λόγω της
λόγω της  συμπεραίνουμε ότι
συμπεραίνουμε ότι  θα είναι
θα είναι  , ως εντός εναλλάξ των ευθειών
, ως εντός εναλλάξ των ευθειών  τεμνομένων υπό της
τεμνομένων υπό της  και συνεπώς
και συνεπώς  .
.