
i) Αν
 είναι η εφαπτομένη της γραφικής παράστασης
είναι η εφαπτομένη της γραφικής παράστασης  της συνάρτησης
της συνάρτησης  στο σημείο
στο σημείο  ,
, να βρείτε το εμβαδόν του χωρίου που περικλείεται από τη
 , την ευθεία
, την ευθεία  και τον άξονα
και τον άξονα  .
.ii) Έστω
 η γωνία που σχηματίζει η
η γωνία που σχηματίζει η  με την ευθεία
με την ευθεία  , όπου
, όπου  είναι η αρχή των αξόνων.
είναι η αρχή των αξόνων. Να εκφράσετε την
 ως συνάρτηση του
ως συνάρτηση του 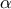 και να βρείτε την μέγιστη τιμή της
και να βρείτε την μέγιστη τιμή της  όταν το
όταν το 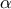 μεταβάλλεται (
μεταβάλλεται ( ).
).β) Αν η συνάρτηση
 είναι παραγωγίσιμη στο διάστημα
είναι παραγωγίσιμη στο διάστημα ![\displaystyle{[1,e]} \displaystyle{[1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/e45e9c214f89168d99bc56eea3406327.png) με
με  και
και  για κάθε
για κάθε ![\displaystyle{x\in [1,e]} \displaystyle{x\in [1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/35d726fceaf96cbfc16b8bd6380e30f9.png) ,
, να αποδείξετε ότι υπάρχει μόνο ένας αριθμός
 τέτοιος ώστε
τέτοιος ώστε 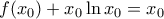
2. α) Στο σύνολο των μιγαδικών αριθμών να βρείτε τις κοινές λύσεις των εξισώσεων
 και
και  .
.β) Θεωρούμε τους μιγαδικούς αριθμούς
 τέτοιους ώστε
τέτοιους ώστε  .
. Να δείξετε ότι αν το
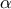 μεταβάλλεται στο
μεταβάλλεται στο  και ισχύει
και ισχύει  , τότε η εικόνα
, τότε η εικόνα  του
του  στο μιγαδικό επίπεδο κινείται σε μια υπερβολή.
στο μιγαδικό επίπεδο κινείται σε μια υπερβολή.3. α) Έστω
 πραγματικός αριθμός
πραγματικός αριθμός  πολυώνυμα με πραγματικούς συντελεστές ώστε
πολυώνυμα με πραγματικούς συντελεστές ώστε  και το
και το  έχει βαθμό μεγαλύτερο ή ίσο του
έχει βαθμό μεγαλύτερο ή ίσο του  .
. Να αποδείξετε ότι υπάρχει πολυώνυμο
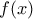 τέτοιο ώστε
τέτοιο ώστε  , αν και μόνο αν
, αν και μόνο αν  .
.β) Έστω
 ακέραιος μεγαλύτερος ή ίσος του
ακέραιος μεγαλύτερος ή ίσος του  .
. Να βρείτε τις τιμές των
 για τις οποίες το πολυώνυμο
για τις οποίες το πολυώνυμο  έχει παράγοντα το
έχει παράγοντα το 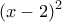 .
.4. α) Να αποδείξετε ότι η εξίσωση της παραβολής με εστία το σημείο
 και διευθετούσα την ευθεία
και διευθετούσα την ευθεία  είναι
είναι  .
.β) Έστω
 θετικός ακέραιος και
θετικός ακέραιος και  ένας δειγματικός χώρος.
ένας δειγματικός χώρος. Δίνονται οι πιθανότητες
 για
για  . Να υπολογίσετε :
. Να υπολογίσετε :i) Την πιθανότητα

ii) Την πιθανότητα
 του ενδεχομένου
του ενδεχομένου 
edit
Διορθώθηκε η φορά της ανισότητας στο 1β

 έχουμε,
έχουμε,

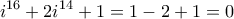






 έχουμε,
έχουμε, 
 ένας μιγαδικός με την παραπάνω ιδιότητα.Τότε,
ένας μιγαδικός με την παραπάνω ιδιότητα.Τότε,

 και ο τύπος
και ο τύπος 


 είναι γεωμετρική πρόοδος με
είναι γεωμετρική πρόοδος με και λόγο
και λόγο 












 στην σχέση
στην σχέση  έχουμε
έχουμε 
![\displaystyle{[A(x).B(x)]'=[(x -\rho )^2.f(x)]'\Rightarrow A'(x).B(x)+A(x).B'(x)=2(x-\rho ).f(x)+f'(x).(x-\rho )^2 (3)} \displaystyle{[A(x).B(x)]'=[(x -\rho )^2.f(x)]'\Rightarrow A'(x).B(x)+A(x).B'(x)=2(x-\rho ).f(x)+f'(x).(x-\rho )^2 (3)}](/forum/ext/geomar/texintegr/latexrender/pictures/29e0bbfd184c3a5f6fb2adddd269b9f7.png)
 την τιμή
την τιμή 
![\displaystyle{\xrightarrow[B(\rho )\neq 0]{A(\rho )=0}A'(\rho )=0 (4)} \displaystyle{\xrightarrow[B(\rho )\neq 0]{A(\rho )=0}A'(\rho )=0 (4)}](/forum/ext/geomar/texintegr/latexrender/pictures/19a2b26c7cce678e4e7ca9719af6717b.png)
 τελικά προκύπτει
τελικά προκύπτει 
 και αφού
και αφού 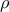 ρίζα του πολυωνύμου
ρίζα του πολυωνύμου  τότε υπάρχει πολυώνυμο
τότε υπάρχει πολυώνυμο 
 Επίσης
Επίσης 
 δηλαδή
δηλαδή  που σημαίνει ότι
που σημαίνει ότι  συνεπώς υπάρχει πολυώνυμο, έστω
συνεπώς υπάρχει πολυώνυμο, έστω  τέτοιο ώστε
τέτοιο ώστε  όπου
όπου  πολυώνυμο το πολύ πρώτου βαθμού.
πολυώνυμο το πολύ πρώτου βαθμού. 
 θα έχουμε τελικά
θα έχουμε τελικά 
 Οπότε συνδυάζοντας αυτό με το ερώτημα α) και αν θέσουμε
Οπότε συνδυάζοντας αυτό με το ερώτημα α) και αν θέσουμε και αφού
και αφού 
 Οπότε υπολογίζουμε τις τιμές αυτές:
Οπότε υπολογίζουμε τις τιμές αυτές:

 προκύπτει το σύστημα:
προκύπτει το σύστημα:

 το σημείο
το σημείο  βρίσκεται στο πρώτο τεταρτημόριο.
βρίσκεται στο πρώτο τεταρτημόριο. στο σημείο
στο σημείο  δίνεται από την σχέση
δίνεται από την σχέση
 στο σημείο
στο σημείο  και τον άξονα
και τον άξονα  στο σημείο
στο σημείο 

![\displaystyle{2[\frac{x^{3}}{3}]_{0}^{2\alpha }-8\alpha [\frac{x^{2}}{2}]_{0}^{2\alpha }+8\alpha ^{3}=\frac{16\alpha ^{3}}{3}, \alpha >0} \displaystyle{2[\frac{x^{3}}{3}]_{0}^{2\alpha }-8\alpha [\frac{x^{2}}{2}]_{0}^{2\alpha }+8\alpha ^{3}=\frac{16\alpha ^{3}}{3}, \alpha >0}](/forum/ext/geomar/texintegr/latexrender/pictures/db9d41c252e2fed4340d55e61cd4fcd5.png)


 θα αναζητήσουμε την παράγωγο της συνάρτησης αυτής,
θα αναζητήσουμε την παράγωγο της συνάρτησης αυτής, 



![\displaystyle{(0,\frac{\sqrt{2}}{8}]} \displaystyle{(0,\frac{\sqrt{2}}{8}]}](/forum/ext/geomar/texintegr/latexrender/pictures/d11638d58ef0e704af513f09367d249b.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο 
 και έχουμε μέγιστη τιμή την
και έχουμε μέγιστη τιμή την  που είναι και η μέγιστη τιμή για την εφαπτομένη της γωνίας
που είναι και η μέγιστη τιμή για την εφαπτομένη της γωνίας  .
.![\displaystyle{g(x)=f(x)+xlnx-x, x\in [1,e]} \displaystyle{g(x)=f(x)+xlnx-x, x\in [1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/2227bdd289fcac52968a462334fd8aad.png)
 είναι συνεχής στο διάστημα
είναι συνεχής στο διάστημα ![[1,e] [1,e]](/forum/ext/geomar/texintegr/latexrender/pictures/84b8350dcaf54462dc964cf2fca7f6c0.png) αφού
αφού  είναι γνωστές συνεχής συανρτήσεις και
είναι γνωστές συνεχής συανρτήσεις και  συνεχής στο παραπάνω
συνεχής στο παραπάνω  αφού
αφού ![\displaystyle{f(x)<1 , x\in [1,e]} \displaystyle{f(x)<1 , x\in [1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/f41237ff123a65635d6b48632f1dc034.png)
 αφού
αφού ![\displaystyle{f(x)>0, x\in[1,e]} \displaystyle{f(x)>0, x\in[1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/ca9c1c3f574d41a8715c3892baf5416c.png)

 αφού
αφού  για κάθε
για κάθε 
 που βρήκαμε παραπάνω, είναι μοναδικό.
που βρήκαμε παραπάνω, είναι μοναδικό.