Άλλες επιθυμητές γνώσεις: Αντίστροφοι modulo p. (Για την απόδειξη.)
Επίπεδο: Απολύτως απαραίτητο σε όσους λαμβάνουν μέρος στον Αρχιμήδη των μεγάλων και πάνω. Το ίδιο και για όσους juniors θα λάβουν μέρος σε διεθνείς διαγωνισμούς.
Θεώρημα Wilson: Έστω φυσικός
 . Ο
. Ο  είναι πρώτος αν και μόνο αν
είναι πρώτος αν και μόνο αν 
Παράδειγμα 1: Είναι
 άρα ο
άρα ο  είναι πρώτος.
είναι πρώτος.Παράδειγμα 2: Είναι
 άρα ο
άρα ο  δεν είναι πρώτος.
δεν είναι πρώτος.Απόδειξη:
Άλλα παραδείγματα:
viewtopic.php?p=44148#p44148
viewtopic.php?p=217680#p217680
viewtopic.php?f=182&t=7328
viewtopic.php?p=147969#p147969
viewtopic.php?p=161782#p161782
viewtopic.php?p=53853#p53853
viewtopic.php?f=182&t=50428 (Άλυτο υποερώτημα)
Προκριματικός Μεγάλων 2015 - Πρόβλημα 1
ΒΜΟ 2016 - Πρόβλημα 3
Άλλη εφαρμογή
Θεώρημα: Αν
 πρώτος με
πρώτος με  τότε υπάρχει
τότε υπάρχει  με
με  .
. Απόδειξη:

 . Ας υποθέσουμε λοιπόν προς άτοπο ότι
. Ας υποθέσουμε λοιπόν προς άτοπο ότι  με
με  . Τότε
. Τότε  . Επειδή
. Επειδή  , άτοπο.
, άτοπο. είναι άμεσο οπότε θα υποθέσουμε ότι
είναι άμεσο οπότε θα υποθέσουμε ότι  . Θα χρησιμοποιήσουμε ότι αν ο
. Θα χρησιμοποιήσουμε ότι αν ο  τότε υπάρχει μοναδικό
τότε υπάρχει μοναδικό  με
με  . (
. ( τότε
τότε  και άρα
και άρα 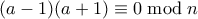 . Δηλαδή
. Δηλαδή  και αφού
και αφού  ή
ή  . Δηλαδή
. Δηλαδή  .
. σε ζεύγη
σε ζεύγη  ώστε
ώστε  τα ζεύγη είναι τα
τα ζεύγη είναι τα  και
και  .] Οπότε πολλαπλασιάζοντας όλους τους αριθμούς του συνόλου
.] Οπότε πολλαπλασιάζοντας όλους τους αριθμούς του συνόλου  . Δηλαδή
. Δηλαδή  και άρα
και άρα  .
. στα ζεύγη
στα ζεύγη  .
.  ισούται με
ισούται με  . Οπότε το γινόμενο των αριθμών όλων των ζευγών ισούται με
. Οπότε το γινόμενο των αριθμών όλων των ζευγών ισούται με ![\displaystyle{ (-1^2)(-2^2) \cdots \left(- ((p-1)/2)^2 \right) \equiv (-1)^{(p-1)/2} \left[ ((p-1)/2)!\right]^2 \equiv \left[\left( \tfrac{p-1}{2} \right)!\right]^2 } \displaystyle{ (-1^2)(-2^2) \cdots \left(- ((p-1)/2)^2 \right) \equiv (-1)^{(p-1)/2} \left[ ((p-1)/2)!\right]^2 \equiv \left[\left( \tfrac{p-1}{2} \right)!\right]^2 }](/forum/ext/geomar/texintegr/latexrender/pictures/32b8738609497f4d014253632c6a824e.png)
 . Άρα μπορούμε να πάρουμε
. Άρα μπορούμε να πάρουμε 