 και αν:
και αν:


να αποδείξετε ότι ή θα είναι
 ή
ή 
 , (1)
, (1) και
και  είναι αρνητικές και άρα για κάθε
είναι αρνητικές και άρα για κάθε  θα είναι:
θα είναι: και
και 
 . Με τον ίδιο τρόπο από τις δύο άλλες εξισώσεις του συστήματος
. Με τον ίδιο τρόπο από τις δύο άλλες εξισώσεις του συστήματος είναι επίσης αριθμοί θετικοί.
είναι επίσης αριθμοί θετικοί.
 , (2)
, (2) είναι
είναι  και αφού
και αφού 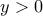 (όπως πιο πάνω είδαμε), τότε από την (2)
(όπως πιο πάνω είδαμε), τότε από την (2)  και
και  είναι ομόσημοι.
είναι ομόσημοι. και
και 
 είναι ομόσημοι.
είναι ομόσημοι. ή θα είναι όλοι μικρότεροι ή ίσοι με το
ή θα είναι όλοι μικρότεροι ή ίσοι με το  .
. , ή
, ή 


 είναι θετικοί και ότι οι αριθμοί
είναι θετικοί και ότι οι αριθμοί  είναι ομόσημοι.
είναι ομόσημοι. , (ομοίως θα εργασθούμε και στις άλλες περιπτώσεις)
, (ομοίως θα εργασθούμε και στις άλλες περιπτώσεις) . Τότε είναι
. Τότε είναι  και άρα
και άρα  .
. έπεται ότι
έπεται ότι  και αφού
και αφού  έπεται ότι
έπεται ότι  .
. . Άρα
. Άρα  και άρα:
και άρα: , που όμως είναι άτοπο αφού η διακρίνουσα
, που όμως είναι άτοπο αφού η διακρίνουσα  είναι αρνητική.
είναι αρνητική. . Τότε
. Τότε  . Και αφού όπως πιο πάνω αποδείξαμε ότι οι αριθμοί
. Και αφού όπως πιο πάνω αποδείξαμε ότι οι αριθμοί  είναι
είναι .
. έπεται ότι
έπεται ότι  και άρα
και άρα  και αφού
και αφού  έπεται ότι
έπεται ότι . Όμως έχουμε ότι
. Όμως έχουμε ότι  και άρα
και άρα 
 , το οποίο πάλι είναι άτοπο αφού η διακρίνουσα
, το οποίο πάλι είναι άτοπο αφού η διακρίνουσα  και τώρα άμεσα έπεται ότι και
και τώρα άμεσα έπεται ότι και  και
και 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες