Μία γρήγορη (ίσως και γνωστή), λίγο πριν ολοκληρωθεί ο οβελίας... Έστω
 το σημείο τομής των διαγωνίων τετραπλεύρου
το σημείο τομής των διαγωνίων τετραπλεύρου  εγγεγραμμένου σε κύκλο κέντρου
εγγεγραμμένου σε κύκλο κέντρου  και
και 
τα περίκεντρα των τριγώνων
 αντίστοιχα. Να δείξετε ότι το
αντίστοιχα. Να δείξετε ότι το 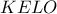 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.Συντονιστές: silouan, Doloros, george visvikis
 το σημείο τομής των διαγωνίων τετραπλεύρου
το σημείο τομής των διαγωνίων τετραπλεύρου  εγγεγραμμένου σε κύκλο κέντρου
εγγεγραμμένου σε κύκλο κέντρου  και
και 
 αντίστοιχα. Να δείξετε ότι το
αντίστοιχα. Να δείξετε ότι το 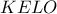 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. είναι η διάκεντρος των δύο κύκλων (περιγεγραμμένοι των
είναι η διάκεντρος των δύο κύκλων (περιγεγραμμένοι των  και
και 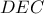 ), επομένως είναι κάθετη στη κοινή χορδή
), επομένως είναι κάθετη στη κοινή χορδή  . (1)
. (1)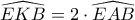 (επίκεντρη-εγγεγραμμένη).
(επίκεντρη-εγγεγραμμένη).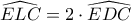 .
. έχουμε ότι
έχουμε ότι  , άρα
, άρα  .
. και
και  είναι όμοια και οι γωνίες
είναι όμοια και οι γωνίες 
 είναι ισογώνια της
είναι ισογώνια της  στο τρίγωνο
στο τρίγωνο 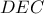 ως προς την κορυφή
ως προς την κορυφή  , άρα η
, άρα η  είναι κάθετη στη
είναι κάθετη στη  (η ευθεία που ενώνει μια κορυφή με το περίκεντρο είναι ισογώνια με το αντίστοιχο ύψος). (2)
(η ευθεία που ενώνει μια κορυφή με το περίκεντρο είναι ισογώνια με το αντίστοιχο ύψος). (2)  .
.  και έτσι το
και έτσι το 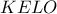 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο.1ος τρόπος:george visvikis έγραψε:Καλό Πάσχα σε όλους!
Μία γρήγορη (ίσως και γνωστή), λίγο πριν ολοκληρωθεί ο οβελίας...
Έστωτο σημείο τομής των διαγωνίων τετραπλεύρου
εγγεγραμμένου σε κύκλο κέντρου
και
τα περίκεντρα των τριγώνων
αντίστοιχα. Να δείξετε ότι το
είναι παραλληλόγραμμο.




 . Από
. Από  παραλληλόγραμμο και το ζητούμενο έχει αποδειχθεί.
παραλληλόγραμμο και το ζητούμενο έχει αποδειχθεί. είναι οι ορθές προβολές του
είναι οι ορθές προβολές του  στις
στις 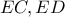 αντίστοιχα (προφανώς
αντίστοιχα (προφανώς  τα μέσα των
τα μέσα των 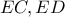 (χορδές του
(χορδές του  αντίστοιχα) τότε
αντίστοιχα) τότε  . Από την
. Από την  σύμφωνα με το Stathis Koutras’ Theorem προκύπτει ότι
σύμφωνα με το Stathis Koutras’ Theorem προκύπτει ότι  και με όμοιο τρόπο προκύπτει ότι
και με όμοιο τρόπο προκύπτει ότι 
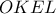 παραλληλόγραμμο και το ζητούμενο έχει αποδειχθεί.
παραλληλόγραμμο και το ζητούμενο έχει αποδειχθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες