 σημείο της βάσης
σημείο της βάσης  ισοσκελούς τριγώνου
ισοσκελούς τριγώνου  ώστε
ώστε  και
και  ένα σημείο του
ένα σημείο του 
Αν
 να δείξετε ότι
να δείξετε ότι 
Συντονιστές: silouan, Doloros, george visvikis
 σημείο της βάσης
σημείο της βάσης  ισοσκελούς τριγώνου
ισοσκελούς τριγώνου  ώστε
ώστε  και
και  ένα σημείο του
ένα σημείο του 
 να δείξετε ότι
να δείξετε ότι 
george visvikis έγραψε:Μιάμισι γωνία.png
Έστωσημείο της βάσης
ισοσκελούς τριγώνου
ώστε
και
ένα σημείο του
Αννα δείξετε ότι
 . Έστω
. Έστω  το κέντρο του
το κέντρο του  η άλλη τομή της ευθείας
η άλλη τομή της ευθείας  μ αυτόν .Επειδή από το εγγεγραμμένο
μ αυτόν .Επειδή από το εγγεγραμμένο  έχω
έχω 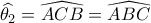 τα
τα 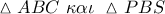 έχουν δύο γωνίες
έχουν δύο γωνίες  ισοσκελές με κορυφή
ισοσκελές με κορυφή  . Μα τότε η ευθεία
. Μα τότε η ευθεία  είναι μεσοκάθετος στο
είναι μεσοκάθετος στο  αφού τα
αφού τα 
 . Ας είναι
. Ας είναι  το σημείο τομής της ευθείας
το σημείο τομής της ευθείας  με τη
με τη  .
. και διχοτόμος της
και διχοτόμος της  . Επειδή
. Επειδή  και άρα
και άρα 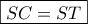 μα τότε και λόγω της προφανούς ισότητας
μα τότε και λόγω της προφανούς ισότητας 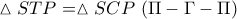 ,
,  δηλαδή :
δηλαδή : .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 22 επισκέπτες