Έστω
 ακολουθία θετικών ακεραίων τέτοια ώστε ο
ακολουθία θετικών ακεραίων τέτοια ώστε ο  είναι το πλήθος των θετικών διαιρετών του
είναι το πλήθος των θετικών διαιρετών του  . Έστω επίσης
. Έστω επίσης  .
. Να αποδειχθεί ότι, για κάποιο
 , ο
, ο  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο. ακολουθία θετικών ακεραίων τέτοια ώστε ο
ακολουθία θετικών ακεραίων τέτοια ώστε ο  είναι το πλήθος των θετικών διαιρετών του
είναι το πλήθος των θετικών διαιρετών του  . Έστω επίσης
. Έστω επίσης  .
.  , ο
, ο  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο. τέτοιο ώστε
τέτοιο ώστε  υπάρχει θετικός ακέραιος
υπάρχει θετικός ακέραιος  τέτοιος ώστε
τέτοιος ώστε να είναι τέλειο τετράγωνο. Είναι σωστή η πρόταση ή λάθος;
να είναι τέλειο τετράγωνο. Είναι σωστή η πρόταση ή λάθος;dement έγραψε:Από μαθητικό διαγωνισμό υπό την αιγίδα (και) της SNS.
Έστωακολουθία θετικών ακεραίων τέτοια ώστε ο
είναι το πλήθος των θετικών διαιρετών του
. Έστω επίσης
.
Να αποδειχθεί ότι, για κάποιο, ο
είναι τέλειο τετράγωνο.
 ισχύει
ισχύει  , όπου
, όπου  , το πλήθος των διαιρετών του
, το πλήθος των διαιρετών του  . Έτσι
. Έτσι  . Ουσιαστικά το πρόβλημα ζητάει να δείξουμε ότι θα υπάρχει
. Ουσιαστικά το πρόβλημα ζητάει να δείξουμε ότι θα υπάρχει  , αφού κάθε τέλειο τετράγωνο έχει περιττό πλήθος διαιρετών. Αν
, αφού κάθε τέλειο τετράγωνο έχει περιττό πλήθος διαιρετών. Αν  περιττός τελειώσαμε. Θα δείξουμε ότι ο τελευταίος όρος
περιττός τελειώσαμε. Θα δείξουμε ότι ο τελευταίος όρος  της ακολουθίας θα είναι το
της ακολουθίας θα είναι το  . Προφανώς, το
. Προφανώς, το  δεν γίνεται να είναι τελευταίος όρος (αφού δεν υπάρχει ακέραιος
δεν γίνεται να είναι τελευταίος όρος (αφού δεν υπάρχει ακέραιος  με έναν διαιρέτη) . Με βάση την πρώτη σχέση κάθε διαδοχικός όρος της ακολουθίας μειώνεται τουλάχιστον κατά ένα. Συνεπώς, αφού
με έναν διαιρέτη) . Με βάση την πρώτη σχέση κάθε διαδοχικός όρος της ακολουθίας μειώνεται τουλάχιστον κατά ένα. Συνεπώς, αφού  . Ο
. Ο  θα είναι ίσος με
θα είναι ίσος με  . Άρα, θα έχει προηγηθεί
. Άρα, θα έχει προηγηθεί 
 με
με  διαιρέτες και
διαιρέτες και  (πρώτος αριθμός
(πρώτος αριθμός 
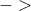 περιττός) .Συνεπώς ο
περιττός) .Συνεπώς ο  , θα είναι τέλειο τετράγωνο,αφού έχει περιττό πλήθος δαιρετών, το ζητούμενο. (όρισα ως
, θα είναι τέλειο τετράγωνο,αφού έχει περιττό πλήθος δαιρετών, το ζητούμενο. (όρισα ως  τον τελευταίο όρο της ακολουθίας, που βέβαια δεν ύπαρχει στην πράξη αφού
τον τελευταίο όρο της ακολουθίας, που βέβαια δεν ύπαρχει στην πράξη αφού  )
) , που φυσικά είναι τέλειο τετράγωνο.
, που φυσικά είναι τέλειο τετράγωνο. θα συμβολίζουμε το πλήθος διαιρετών του
θα συμβολίζουμε το πλήθος διαιρετών του 
 με την ισότητα να ισχύει μόνο όταν
με την ισότητα να ισχύει μόνο όταν 
![p\in[x,2x] p\in[x,2x]](/forum/ext/geomar/texintegr/latexrender/pictures/79c0a9b59acd0efc15e4f688c2b8dbb4.png) για κάθε
για κάθε  ο οποίος δεν θα διαιρούσε τους:
ο οποίος δεν θα διαιρούσε τους: 
 άρα
άρα  .
. αν και μόνο αν
αν και μόνο αν  .
. .
. . Παίρνοντας όριο στο
. Παίρνοντας όριο στο  καταλήγουμε σε άτοπο.
καταλήγουμε σε άτοπο. πρέπει
πρέπει  , άρα
, άρα 
 όπου
όπου 
 δίνει ότι ο
δίνει ότι ο  πρέπει να είναι πρώτος αριθμός, έστω
πρέπει να είναι πρώτος αριθμός, έστω 
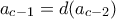 οπότε με την ίδια διαδικασία προκύπτει ότι
οπότε με την ίδια διαδικασία προκύπτει ότι  όπου
όπου  πρώτος αριθμός.
πρώτος αριθμός. είναι άρτιος αφού
είναι άρτιος αφού  οπότε ο αριθμός
οπότε ο αριθμός  είναι τέλειο τετράγωνο. Αν
είναι τέλειο τετράγωνο. Αν  τότε το ζητούμενο έπεται.
τότε το ζητούμενο έπεται. είναι θετικοί ακέραιοι με
είναι θετικοί ακέραιοι με 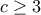
Ναι, απλά υπέθεσα ότιdement έγραψε:Πολύ ωραία. Να προσθέσω μόνο ότι υπάρχει και η περίπτωση της σταθερής ακολουθίας με τιμή, που φυσικά είναι τέλειο τετράγωνο.

 είναι φθίνουσα. Έστω
είναι φθίνουσα. Έστω  .
. (οι μόνοι αριθμοί με
(οι μόνοι αριθμοί με  ). Αν
). Αν  τελειώσαμε. Αν
τελειώσαμε. Αν  τότε
τότε  από την υπόθεση. Ο
από την υπόθεση. Ο  είναι περιττός (πρώτος) και ο
είναι περιττός (πρώτος) και ο 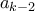 τέλειο τετράγωνο.
τέλειο τετράγωνο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες