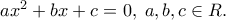 Δίνεται επιπλέον ότι
Δίνεται επιπλέον ότι 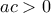 και
και 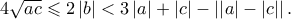
Να αποδείξετε ότι εξίσωση αυτή έχει πραγματικές ρίζες με απόλυτη τιμή μικρότερη της μονάδας.
Συντονιστές: achilleas, emouroukos, silouan
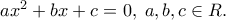 Δίνεται επιπλέον ότι
Δίνεται επιπλέον ότι 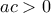 και
και 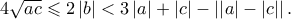
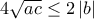 έχουμε ότι η διακρίνουσα είναι μη αρνητική.
έχουμε ότι η διακρίνουσα είναι μη αρνητική.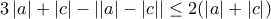
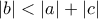
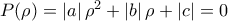
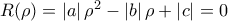
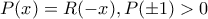
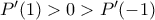
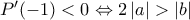
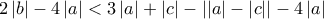
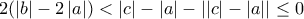
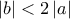 όπως θέλαμε.
όπως θέλαμε.Άριστη Σκέψη και Άμεσα αντανακλαστικά για την ηλικία σου.∫ot.T. έγραψε: ↑Πέμ Μαρ 21, 2024 3:36 pmΑπό την ανισότηταέχουμε ότι η διακρίνουσα είναι μη αρνητική.
Άρα η εξίσωση έχει πραγματικές ρίζες.
Επιπλέον
Άρα
Ανάλογα με το πρόσημο του b θα έχουμε δύο περιπτώσεις για τις ρίζες:
Παρατηρούμε ότι
Εδώ, για να αποδειχθεί το ζητούμενο, αρκεί
Το πρώτο σκέλος είναι προφανές. Για το δεύτερο:
Αρκεί
Όμως
Άρα
Άραόπως θέλαμε.
Παρόμοια με το μέλος ∫ot.T. παραπάνω, αλλά θεωρώντας γνωστή την θεωρία δευτεροβάθμιου τριώνυμου. Η δοθείσα εξίσωση έχει ρίζες με απόλυτη τιμή μικρότερη της μονάδας αν και μόνο αν ικανοποιούνται οι συνθήκεςS.E.Louridas έγραψε: ↑Τετ Μαρ 20, 2024 10:16 pmΘεωρούμε την εξίσωσηΔίνεται επιπλέον ότι
και
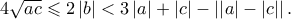
Να αποδείξετε ότι εξίσωση αυτή έχει πραγματικές ρίζες με απόλυτη τιμή μικρότερη της μονάδας.
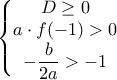 και
και 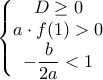
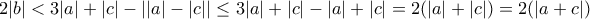 , η τελευταία ισότητα επειδή
, η τελευταία ισότητα επειδή  ομόσημοι αριθμοί (
ομόσημοι αριθμοί (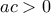 ). Οπότε
). Οπότε 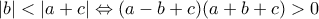 .
.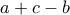 και
και  είναι ομόσημοι. Αν αυτοί οι αριθμοί είναι ετερόσημοι με τον
είναι ομόσημοι. Αν αυτοί οι αριθμοί είναι ετερόσημοι με τον  , τότε θα έχουμε
, τότε θα έχουμε 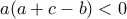 και
και 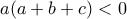 , οπότε αθροίζοντας τις ανισώσεις θα έχουμε
, οπότε αθροίζοντας τις ανισώσεις θα έχουμε 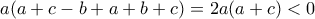 . Όμως οι
. Όμως οι  άρα και ο
άρα και ο  είναι ομόσημοι. 'Ατοπο. Οπότε θα ισχύει
είναι ομόσημοι. 'Ατοπο. Οπότε θα ισχύει 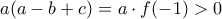 και
και 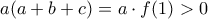 .
.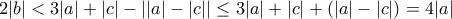 , όπου έγινε χρήση της
, όπου έγινε χρήση της 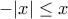 , για
, για 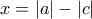 . Οπότε έχουμε διαδοχικά
. Οπότε έχουμε διαδοχικά 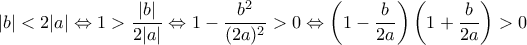
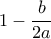 και
και 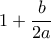 , είναι ομόσημοι. Αν είναι και οι δύο αρνητικοί, τότε θα έχουμε
, είναι ομόσημοι. Αν είναι και οι δύο αρνητικοί, τότε θα έχουμε 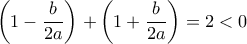 . 'Ατοπο. Άρα αυτοί οι αριθμοί είναι θετικοί. Οπότε
. 'Ατοπο. Άρα αυτοί οι αριθμοί είναι θετικοί. Οπότε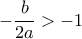 και
και 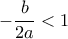
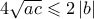 , έχουμε
, έχουμε 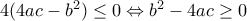 . Δηλαδή
. Δηλαδή  .
. , τηρούνται.
, τηρούνται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης