 και την ελάχιστη τιμή του
και την ελάχιστη τιμή του  ώστε για κάθε
ώστε για κάθε 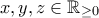 να ισχύει
να ισχύει 
Συντονιστές: achilleas, emouroukos, silouan
 και την ελάχιστη τιμή του
και την ελάχιστη τιμή του  ώστε για κάθε
ώστε για κάθε 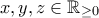 να ισχύει
να ισχύει 
Τοsocrates έγραψε:Να βρείτε τη μέγιστη τιμή τουκαι την ελάχιστη τιμή του
ώστε για κάθε
να ισχύει

 έχουμε ισότητα.
έχουμε ισότητα. (το βρήκα κλέβοντας)
(το βρήκα κλέβοντας) έχουμε ισότητα.
έχουμε ισότητα.



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες