Για τους διαφορετικούς μεταξύ τους θετικούς ακέραιους
 να αποδείξετε ότι ισχύει η ανισότητα
να αποδείξετε ότι ισχύει η ανισότητα
Υπάρχουν φυσικοί που να ικανοποιούν την ισότητα;
Μαθηματική Ολυμπιάδα Μόσχας 1982, 5ο θέμα της 8ης τάξης.
Συντονιστές: achilleas, emouroukos, silouan
 να αποδείξετε ότι ισχύει η ανισότητα
να αποδείξετε ότι ισχύει η ανισότητα
ΧΡΟΝΙΑ ΠΟΛΛΑ Αλέξαντρε.Al.Koutsouridis έγραψε: ↑Τετ Δεκ 27, 2017 12:20 pmΜε αφορμή το θέμα εδώ.
Για τους διαφορετικούς μεταξύ τους θετικούς ακέραιουςνα αποδείξετε ότι ισχύει η ανισότητα
Υπάρχουν φυσικοί που να ικανοποιούν την ισότητα;
Μαθηματική Ολυμπιάδα Μόσχας 1982, 5ο θέμα της 8ης τάξης.
 δύναμη αντί
δύναμη αντί  ;
;Χρόνια Πολλά κ.Σταύρο! Ναι η παρένθεση στο δεύτερο μέλος είναι στο τετράγωνο. Το διόρθωσα και στην αριχική ανάρτηση. Ευχαριστώ για την επισήμανση.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Δεκ 27, 2017 12:53 pmΧΡΟΝΙΑ ΠΟΛΛΑ Αλέξαντρε.
Μήπως δεξιά έχουμεδύναμη αντί
;
Την ισότητα την είδαμε στην παραπομπή, γιαAl.Koutsouridis έγραψε: ↑Τετ Δεκ 27, 2017 12:20 pmΜε αφορμή το θέμα εδώ.
Για τους διαφορετικούς μεταξύ τους θετικούς ακέραιουςνα αποδείξετε ότι ισχύει η ανισότητα
Υπάρχουν φυσικοί που να ικανοποιούν την ισότητα;
 .
.  . Έστω
. Έστω  όπου
όπου  για οποιουσδήποτε δεδομένους διαφορετικούς μεταξύ τους
για οποιουσδήποτε δεδομένους διαφορετικούς μεταξύ τους  το πλήθος φυσικούς. Χωρίς βλάβη
το πλήθος φυσικούς. Χωρίς βλάβη 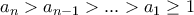 .
.  η αντίστοιχη παράσταση με έναν ακόμη όρο
η αντίστοιχη παράσταση με έναν ακόμη όρο  . Θα δείξουμε
. Θα δείξουμε 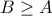 και τελειώσαμε. Το αποδεικτέο ισοδυναμεί με
και τελειώσαμε. Το αποδεικτέο ισοδυναμεί με  που ισοδυναμεί με
που ισοδυναμεί με  , ισοδύναμα
, ισοδύναμα  , ισοδύναμα
, ισοδύναμα  .
.  οπότε
οπότε  που είναι το αριστερό μέλος της
που είναι το αριστερό μέλος της  .
. . Γράφω το δεξί μέλος ως
. Γράφω το δεξί μέλος ως![\displaystyle \sum_{k=1}^n \left[2a_k^6 + 4a_k^3(a_1^3 + \cdots + a_{k-1}^3)\right] \displaystyle \sum_{k=1}^n \left[2a_k^6 + 4a_k^3(a_1^3 + \cdots + a_{k-1}^3)\right]](/forum/ext/geomar/texintegr/latexrender/pictures/ebd94334c08f0edef92d2bacb99cc1f9.png)
 , τότε
, τότε ![\displaystyle \begin{aligned}
\left[2a_k^6 + 4a_k^3(a_1^3 + \cdots + a_{k-1}^3)\right] &\leqslant 2m^6 + 4m^3\left((1^3 + \cdots + (m-1)^3\right) \\
&= 2m^6 + 4m^3 \left(\frac{(m-1)m}{2}\right)^2 \\
&= 2m^6 + m^5(m-1)^2 \\
&= m^5 + m^7 \\
&= a_k^5 + a_k^7
\end{aligned}
\displaystyle \begin{aligned}
\left[2a_k^6 + 4a_k^3(a_1^3 + \cdots + a_{k-1}^3)\right] &\leqslant 2m^6 + 4m^3\left((1^3 + \cdots + (m-1)^3\right) \\
&= 2m^6 + 4m^3 \left(\frac{(m-1)m}{2}\right)^2 \\
&= 2m^6 + m^5(m-1)^2 \\
&= m^5 + m^7 \\
&= a_k^5 + a_k^7
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/5720fcd171b264aef14ff0fedd82237d.png)
 , θέλουμε
, θέλουμε  .)
.)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες