 τυχόν σημείο της πλευράς
τυχόν σημείο της πλευράς  τετραγώνου
τετραγώνου  κέντρου
κέντρου  και ας είναι
και ας είναι  το σημείο τομής της εκ του
το σημείο τομής της εκ του  καθέτου στην
καθέτου στην  με την
με την  . Αν
. Αν  είναι τα σημεία τομής της καθέτου επί την
είναι τα σημεία τομής της καθέτου επί την  στο
στο  με τις ευθείες
με τις ευθείες  αντίστοιχα να δειχθεί ότι η
αντίστοιχα να δειχθεί ότι η  διχοτομεί τη γωνία
διχοτομεί τη γωνία  όπου
όπου  .
.Στάθης
Υ.Σ. Μήπως έχουμε ένα διαφορετικό τρόπο της κατασκευής αυτής

 η τομή των ευθειών
η τομή των ευθειών  και
και  το σημείο τομής των
το σημείο τομής των  επειδή στο τραπέζιο
επειδή στο τραπέζιο 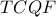 το
το  . Τότε όμως όπως έδειξα στη άσκηση της
. Τότε όμως όπως έδειξα στη άσκηση της  αλλά από το τραπέζιο
αλλά από το τραπέζιο  η διάμεσος του
η διάμεσος του  και άρα
και άρα  . Μα αφού
. Μα αφού 
 θα διχοτομεί τη γωνία
θα διχοτομεί τη γωνία 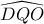 .
. και σύμφωνα με την απόδειξη (και πάλι του
και σύμφωνα με την απόδειξη (και πάλι του  θα εφάπτεται του κύκλου
θα εφάπτεται του κύκλου  το ίδιο και η
το ίδιο και η  (αφού η
(αφού η  είναι μεσοκάθετη της
είναι μεσοκάθετη της  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. στο
στο  Έστω
Έστω  η πλευρά του τετραγώνου,
η πλευρά του τετραγώνου, 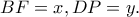 Προφανώς
Προφανώς  είναι το μέσο της
είναι το μέσο της 
 δηλαδή
δηλαδή 






 και νόμο συνημιτόνων στο
και νόμο συνημιτόνων στο 


 Τέλος Π. Θ στο
Τέλος Π. Θ στο 


 και η
και η  . Άρα πράγματι, από αυτή την κατασκευή προκύπτει και η κατασκευή της παραπομπής.
. Άρα πράγματι, από αυτή την κατασκευή προκύπτει και η κατασκευή της παραπομπής.
 και ας είναι
και ας είναι  οι ορθές προβολές του
οι ορθές προβολές του  στις
στις 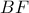 και
και  (σε μήκη) αντίστοιχα .
(σε μήκη) αντίστοιχα .  και
και  θα είναι προφανώς
θα είναι προφανώς  . Ετσι
. Ετσι  και
και 


 σύμφωνα με το
σύμφωνα με το  σημεία κύκλου διαμέτρου
σημεία κύκλου διαμέτρου  (προφανώς κέντρου
(προφανώς κέντρου  διχοτόμος της
διχοτόμος της  .
.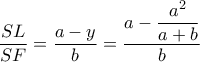
 (όπου
(όπου  το μέσο της
το μέσο της  ) πράγμα που επιβεβαιώνει την παρατήρηση του
) πράγμα που επιβεβαιώνει την παρατήρηση του  .
. ,
, 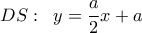 ,
,  , οπότε
, οπότε  .
.
 , άρα
, άρα  .
. και
και  .
. , άρα η
, άρα η  .
.