 τρίγωνο με ορθόκεντρο
τρίγωνο με ορθόκεντρο  και περιγεγράμμενο κύκλο
και περιγεγράμμενο κύκλο  κέντρου
κέντρου  .
.Έστω ότι ο κύκλος με διάμετρο
 τέμνει τον
τέμνει τον  στο σημείο
στο σημείο  .
.Να δείξετε ότι

Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, rek2
 τρίγωνο με ορθόκεντρο
τρίγωνο με ορθόκεντρο  και περιγεγράμμενο κύκλο
και περιγεγράμμενο κύκλο  κέντρου
κέντρου  .
. τέμνει τον
τέμνει τον  στο σημείο
στο σημείο  .
.
 τα ύψη του τριγώνου
τα ύψη του τριγώνου  . Αφού
. Αφού  , έχουμε πως ο κύκλος με διάμετρο
, έχουμε πως ο κύκλος με διάμετρο  περνάει από τα
περνάει από τα  , δηλαδή είναι ο περιγεγραμμένος κύκλος του
, δηλαδή είναι ο περιγεγραμμένος κύκλος του  .
.  έχουμε πως
έχουμε πως  . Όμοια έχουμε πως
. Όμοια έχουμε πως  , επομένως
, επομένως  .
.  και δύναμη
και δύναμη  .
.  πάει στο
πάει στο  , το
, το  στο
στο  και το
και το  στο
στο  . Επομένως ο περιγεγραμμένος κύκλος του
. Επομένως ο περιγεγραμμένος κύκλος του  γίνεται ο περιγεγραμμένος κύκλος του
γίνεται ο περιγεγραμμένος κύκλος του  , δηλαδή ο κύκλος
, δηλαδή ο κύκλος  του
του  .
.  πάει στο
πάει στο  και το
και το  πάει στο
πάει στο  . Επομένως ο περιγεγραμμένος κύκλος του
. Επομένως ο περιγεγραμμένος κύκλος του  γίνεται η ευθεία
γίνεται η ευθεία  . Συνεπώς το σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων
. Συνεπώς το σημείο τομής των περιγεγραμμένων κύκλων των τριγώνων  και
και  , δηλαδή το
, δηλαδή το  , έχει αντίστροφο το σημείο τομής της
, έχει αντίστροφο το σημείο τομής της  με τον κύκλο
με τον κύκλο  του
του  . Αφού όμως το σημείο αυτό είναι διάφορο του
. Αφού όμως το σημείο αυτό είναι διάφορο του  , έπεται πως το αντίστροφο του
, έπεται πως το αντίστροφο του  είναι το μέσο
είναι το μέσο  του
του  .
. είναι συνευθειακά.
είναι συνευθειακά.  αντίστροφα, θα ισχύει ότι
αντίστροφα, θα ισχύει ότι  . Επομένως τα
. Επομένως τα  και
και  είναι εγγράψιμα τετράπλευρα.
είναι εγγράψιμα τετράπλευρα. και
και  . Λόγω του ότι τα τρίγωνα
. Λόγω του ότι τα τρίγωνα 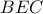 και
και  είναι ορθογώνια και το
είναι ορθογώνια και το  είναι το μέσο του
είναι το μέσο του  , έχουμε πως
, έχουμε πως  , άρα
, άρα  . Όμοια έχουμε πως
. Όμοια έχουμε πως  , άρα
, άρα  .
.  και
και  είναι όμοια. Παρομοίως και τα τρίγωνα
είναι όμοια. Παρομοίως και τα τρίγωνα  και
και  είναι όμοια. Με άλλα λόγια
είναι όμοια. Με άλλα λόγια  και
και  . Όμως
. Όμως  , άρα
, άρα  που είναι το ζητούμενο.
που είναι το ζητούμενο. το αντιδιαμετρικό του
το αντιδιαμετρικό του  . Επειδή το τετράπλευρο
. Επειδή το τετράπλευρο  είναι
είναι  αληθές αφού
αληθές αφού  οι
οι 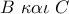 από την
από την  .
.Καλησπέρα Ορέστη,Νίκο ,ΔιονύσηΟρέστης Λιγνός έγραψε:Έστωτρίγωνο με ορθόκεντρο
και περιγεγράμμενο κύκλο
κέντρου
.
Έστω ότι ο κύκλος με διάμετροτέμνει τον
στο σημείο
.
Να δείξετε ότι
ORESTIS.png


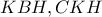 είναι όμοια και συνεπώς
είναι όμοια και συνεπώς 
ΑνSTOPJOHN έγραψε:Καλησπέρα Ορέστη,Νίκο ,ΔιονύσηΟρέστης Λιγνός έγραψε:Έστωτρίγωνο με ορθόκεντρο
και περιγεγράμμενο κύκλο
κέντρου
.
Έστω ότι ο κύκλος με διάμετροτέμνει τον
στο σημείο
.
Να δείξετε ότι
ORESTIS.png
Ισχυουν οι ισότητες των εγεγραμμενων γωνιών που βαίνουν στο ίδιο τόξο
Aρα
Τα τρίγωναείναι όμοια και συνεπώς
Γιάννης
 τότε στο σχήμα το Νίκου το
τότε στο σχήμα το Νίκου το είναι ρόμβος
είναι ρόμβοςΚαλησπέρα θα γίνει επανέλεγχος στις πράξεις ,αυριο ,και αν μου ξέφυγε κάτι θα διορθωθει .Ευχαριστωmikemoke έγραψε:ΑνSTOPJOHN έγραψε:Καλησπέρα Ορέστη,Νίκο ,ΔιονύσηΟρέστης Λιγνός έγραψε:Έστωτρίγωνο με ορθόκεντρο
και περιγεγράμμενο κύκλο
κέντρου
.
Έστω ότι ο κύκλος με διάμετροτέμνει τον
στο σημείο
.
Να δείξετε ότι
ORESTIS.png
Ισχυουν οι ισότητες των εγεγραμμενων γωνιών που βαίνουν στο ίδιο τόξο
Aρα
Τα τρίγωναείναι όμοια και συνεπώς
Γιάννηςτότε στο σχήμα το Νίκου το
είναι ρόμβος
Γεια σου Ορέστη μια λύση ακόμηΟρέστης Λιγνός έγραψε:Έστωτρίγωνο με ορθόκεντρο
και περιγεγράμμενο κύκλο
κέντρου
.
Έστω ότι ο κύκλος με διάμετροτέμνει τον
στο σημείο
.
Να δείξετε ότι
ORESTIS.png

 είναι όμοια ,γιατί
είναι όμοια ,γιατί 
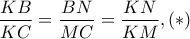



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης